如何在 spss 中创建和解释 qq 图

QQ 图是“分位数-分位数”的缩写，通常用于评估变量是否服从正态分布。

本教程介绍如何在 SPSS 中创建和解释 QQ 图。

示例：SPSS 中的 QQ 图

假设 SPSS 中有以下数据集，显示 25 名不同篮球运动员每场比赛的得分：

我们可以使用SPSS中的以下步骤创建QQ图来判断变量点是否服从正态分布。

步骤 1：选择探索选项。

单击分析选项卡，然后单击描述性统计，然后单击浏览：

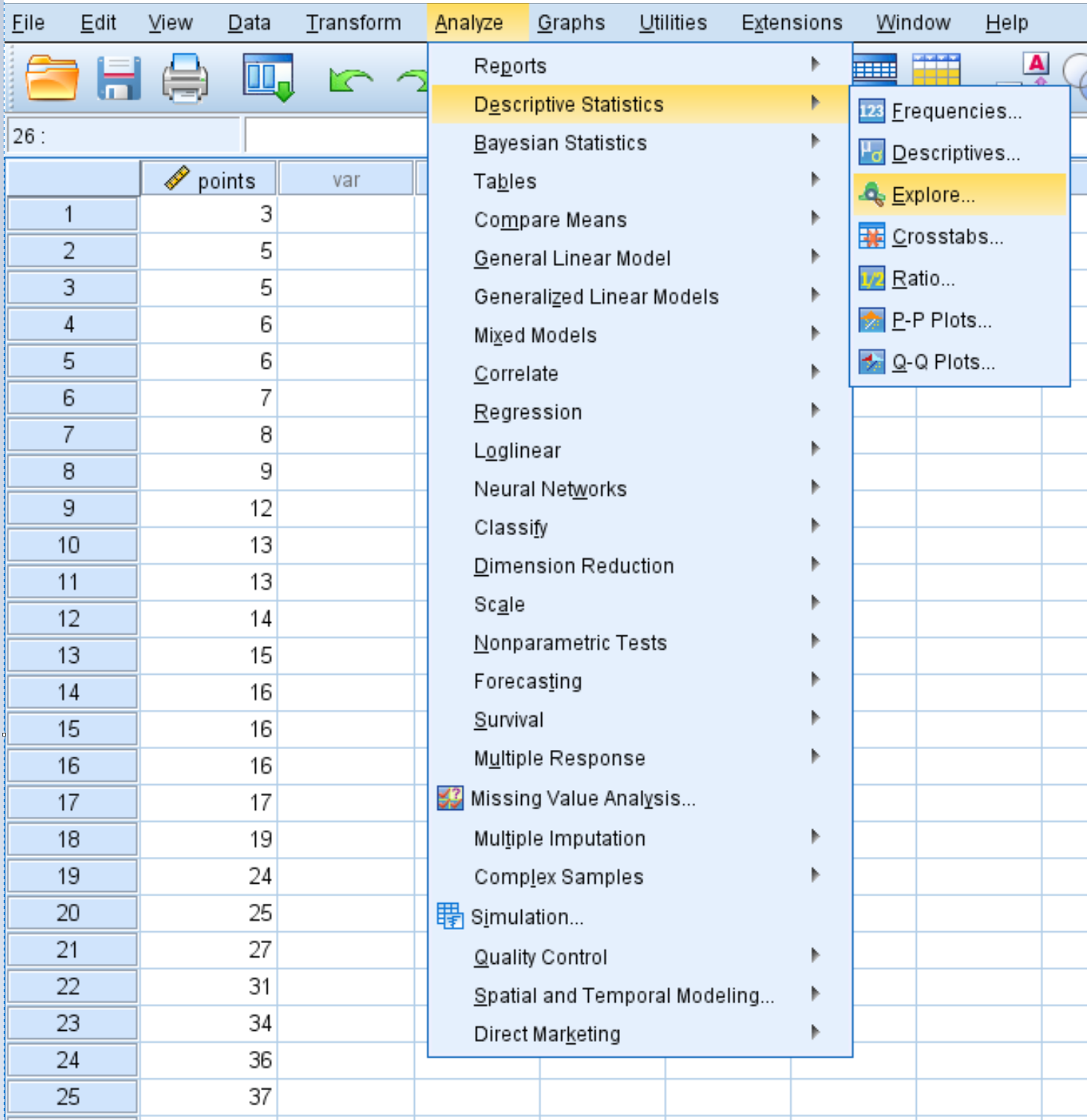
第 2 步：创建 QQ 图。

将变量点拖到标记为“从属列表”的区域中。然后单击标记为“图”的按钮，并确保选中“带检验的正态图”旁边的框。然后单击“继续” 。然后单击“确定” 。

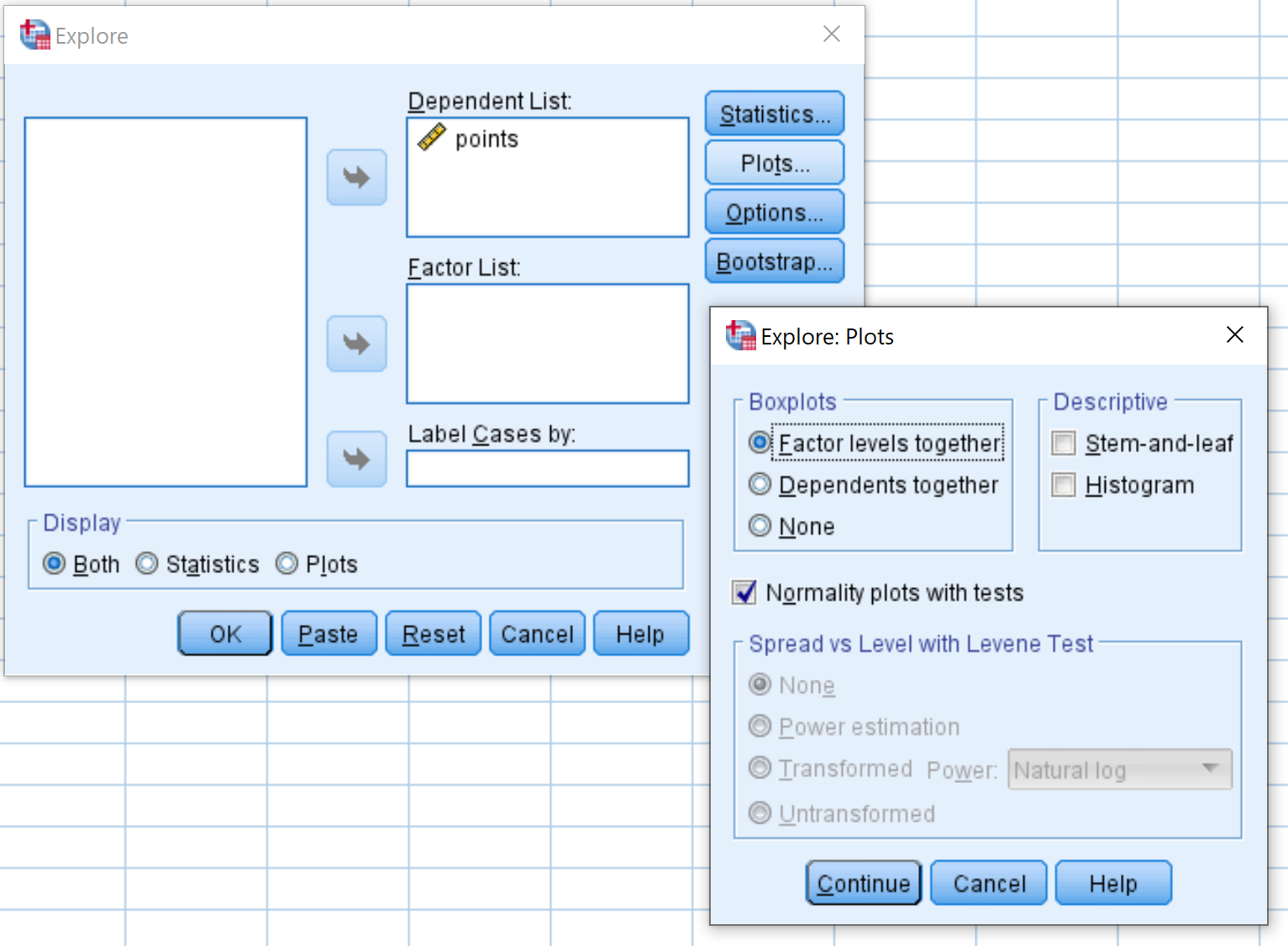
第三步：解读QQ图。

单击“确定”后，将显示以下QQ图：

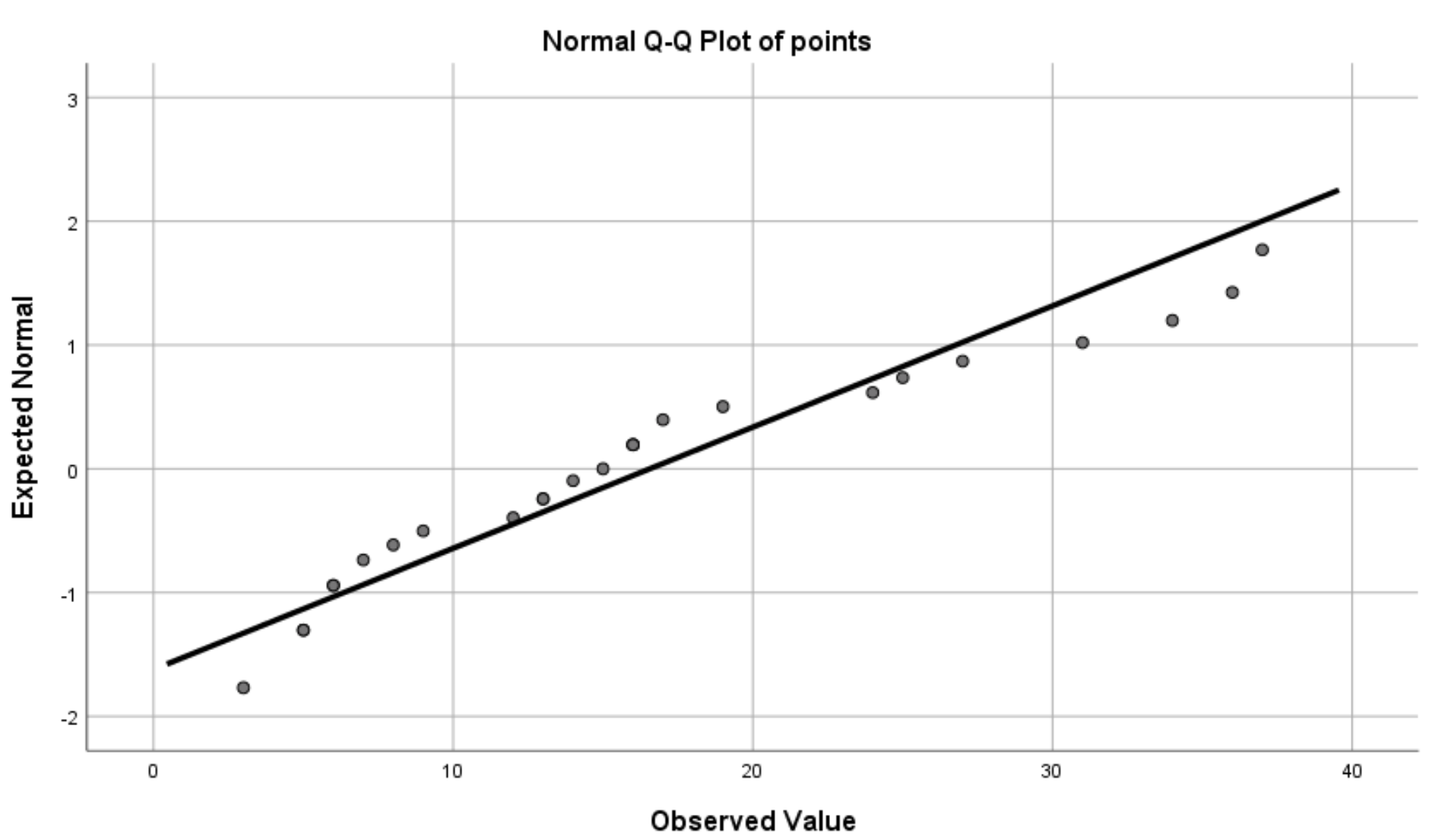
QQ 图背后的想法很简单：如果残差大致遵循 45 度角的直线，则残差大致呈正态分布。

我们可以在上面的 QQ 图中看到，残差往往会稍微偏离 45 度线，尤其是在末端，这可能表明它们不是正态分布的。

虽然 QQ 图不是正式的统计测试，但它提供了一种简单的方法来直观地检查残差是否呈正态分布。

对于两个正式的统计检验，请参见 QQ 图上方显示的 Kolmogorov-Smirnov 检验和 Shapiro-Wilk 检验 p 值：

• Kolmogorov-Smirnov 正态性检验 P 值： 0.086
• Shapiro-Wilk 正态性检验 P 值： 0.042

由于这两个值接近0.05，这表明变量点可能不是正态分布的。