如何在 python 中执行三次回归

三次回归是一种回归类型，当变量之间的关系是非线性时，我们可以使用它来量化预测变量和响应变量之间的关系。

本教程介绍如何在 Python 中执行三次回归。

示例：Python 中的三次回归

假设我们有以下 pandas DataFrame，其中包含两个变量（x 和 y）：

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

如果我们对这些数据制作一个简单的散点图，我们可以看到两个变量之间的关系是非线性的：

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

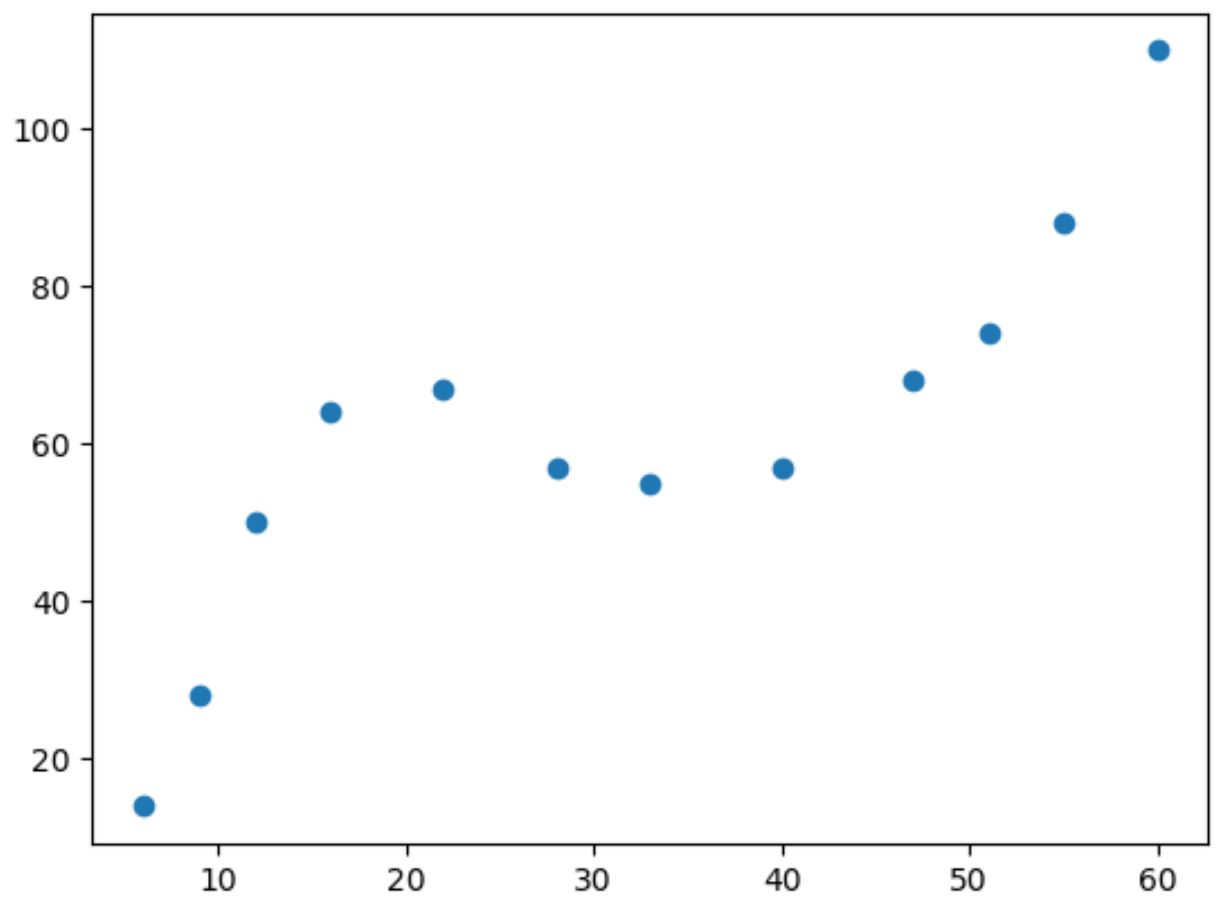
随着 x 值的增加，y 增加到某个点，然后减少，然后再次增加。

图中具有两条“曲线”的模式表明两个变量之间存在立方关系。

这意味着三次回归模型是量化两个变量之间关系的良好候选模型。

要执行三次回归，我们可以使用numpy.polyfit()函数拟合 3 次多项式回归模型：

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

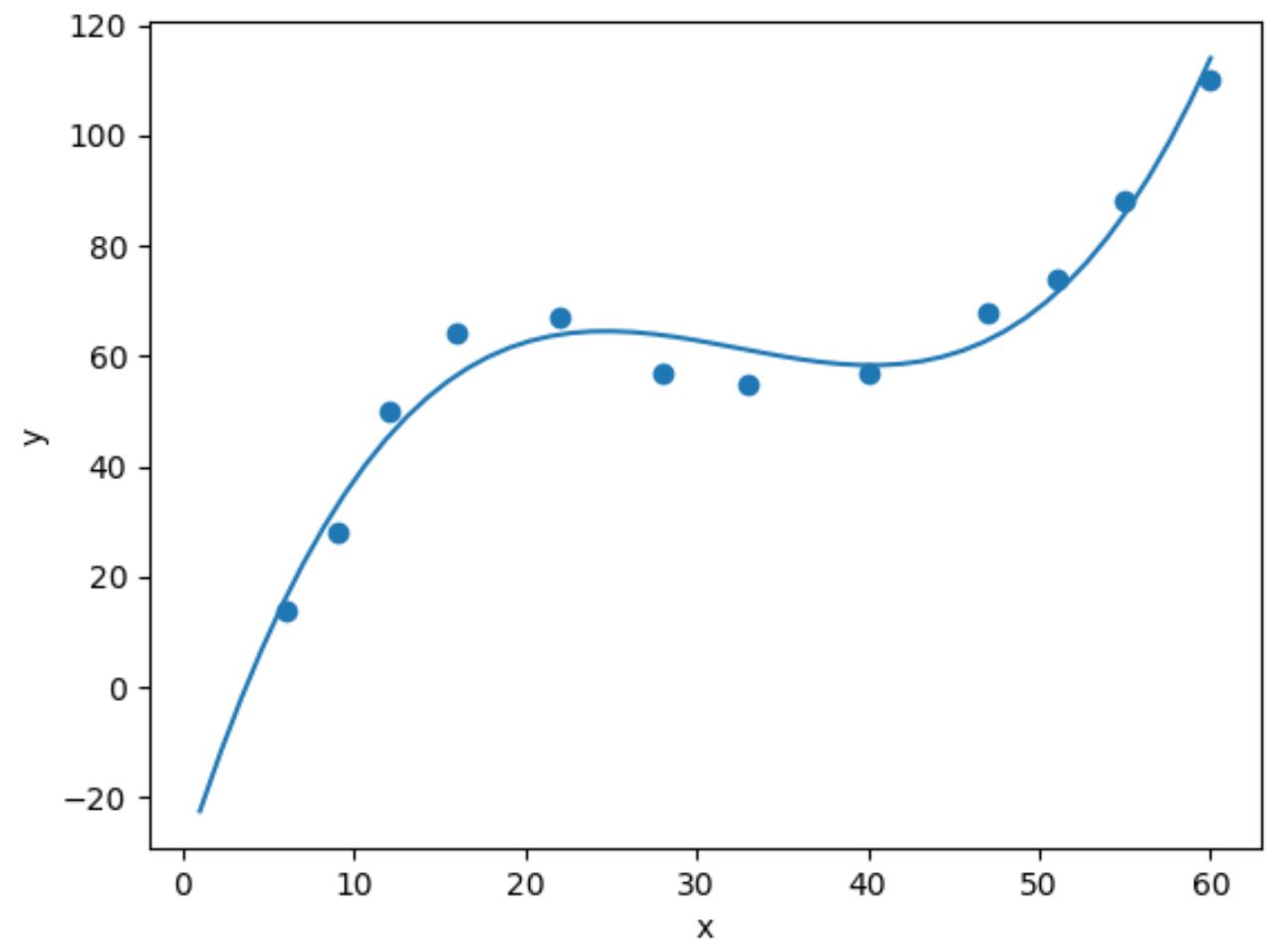
我们可以通过打印模型系数得到拟合的三次回归方程：

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

拟合的三次回归方程为：

y = 0.003302(x) ³ – 0.3214(x) ² + 9.832x – 30.01

我们可以使用这个方程根据 x 的值计算 y 的期望值。

例如，如果 x 为 30，则 y 的预期值为 64.844：

y = 0.003302(30) ³ – 0.3214(30) ² + 9.832(30) – 30.01 = 64.844

我们还可以编写一个简短的函数来获取模型的 R 平方，它是响应变量中可以由预测变量解释的方差的比例。

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

在此示例中，模型的 R 方为0.9632 。

这意味着响应变量中 96.32% 的变异可以由预测变量来解释。

由于这个值如此之高，它告诉我们三次回归模型很好地量化了两个变量之间的关系。

相关：什么是好的 R 平方值？

其他资源

以下教程解释了如何在 Python 中执行其他常见任务：

如何在 Python 中执行简单线性回归
如何在 Python 中执行二次回归
如何在 Python 中执行多项式回归