上栅栏和下栅栏：定义和示例

在统计学中，上限和下限表示数据集中异常值上限和下限的阈值。它们的计算方法如下：

• 最低收盘价= Q1 – (1.5*IQR)
• 收盘上限= Q3 + (1.5*IQR)

其中 IQR 代表“四分位距”，表示数据集中第 75 个百分位 (Q3) 和第 25 个百分位 (Q1) 之间的差异。

位于上屏障上方或下屏障下方的观测值通常被视为异常值。

示例：上下围栏的计算

假设我们有以下数据集：

 Dataset: 11, 13, 14, 14, 15, 16, 18, 22, 24, 27, 34, 36, 38, 41, 45

我们可以使用以下步骤来计算数据集的上下栅栏：

步骤 1：搜索 Q1 和 Q3。

Q1 代表数据集的第 25 个百分位数，Q3 代表第 75 个百分位数。根据四分位数范围计算器，该数据集的 Q1 和 Q3 为：

• 第一航站： 14
• 第三航站楼： 36

步骤 2：找到 IQR（四分位数间距）。

四分位距表示 Q3 和 Q1 之间的差异，计算公式如下：

• 四分位数： Q3 – Q1 = 36 – 14 = 22

第三步：找到上栅栏和下栅栏

我们可以用下面的公式来计算上栅栏和下栅栏：

• 较低收盘价： Q1 – (1.5*IQR) = 14 – (1.5*22) = -19
• 上栅栏： Q3 + (1.5*IQR) = 36 + (1.5*22) = 69

由于我们的数据集中没有任何观测值低于下栅栏或高于上栅栏，因此没有任何观测值被视为异常值。

我们还可以创建一个箱线图来可视化我们的数据值分布以及上下栅栏：

奖励：上下收盘价计算器

无需手动计算数据集的顶部和底部栅栏，您可以随意使用顶部和底部栅栏计算器：

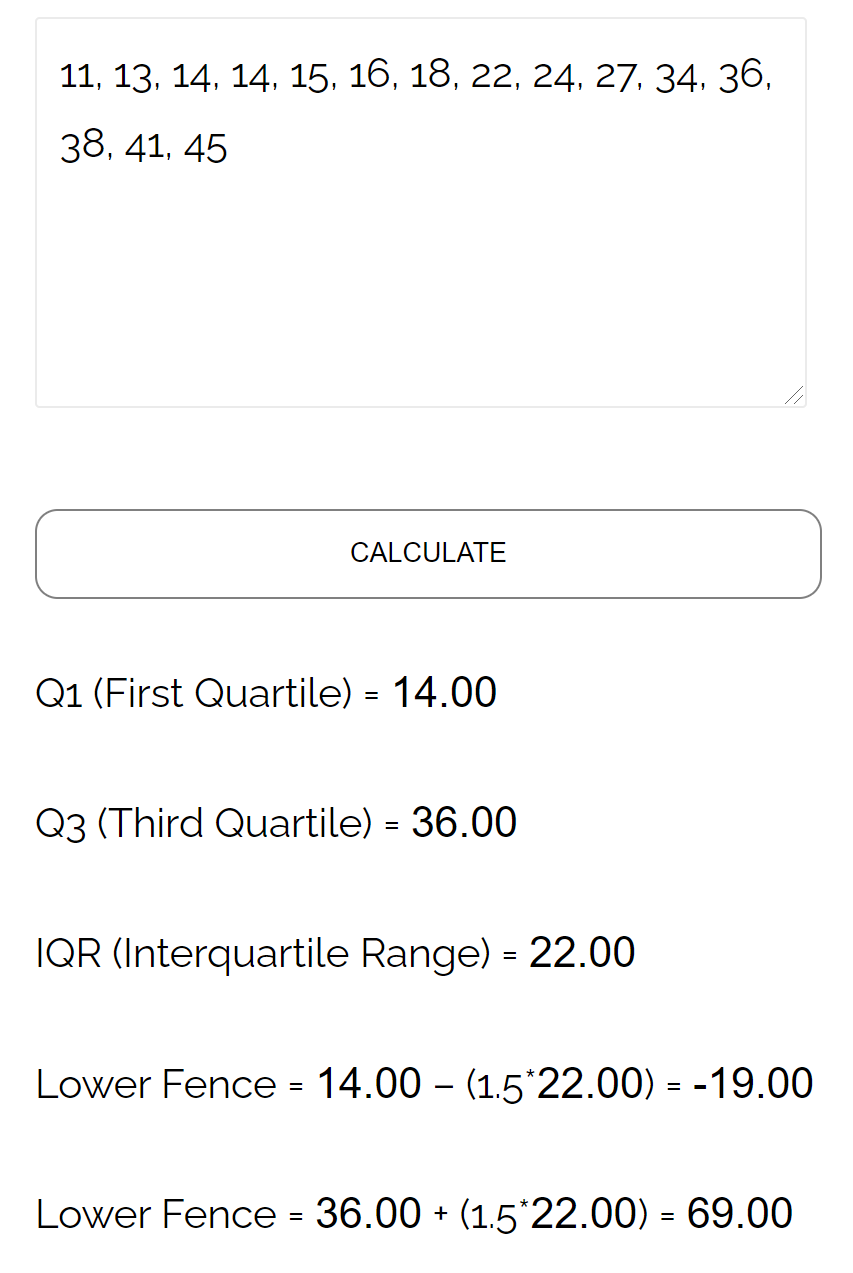
您可以在此页面上找到更多有用的统计计算器。