如何解释统计学中的不对称性：举例
在统计学中，我们使用偏度来描述分布的对称性。
如果数据值的分布在分布的左侧有“尾部”，我们就说它是倾斜的：
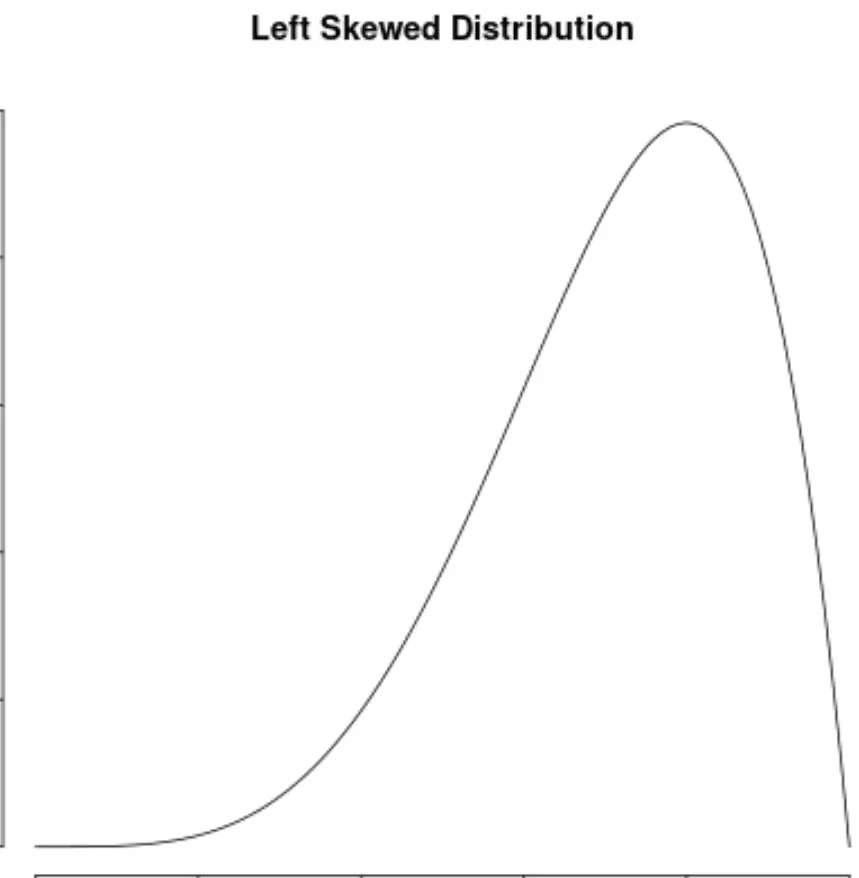
如果分布的右侧有“尾部”，则称该分布是右偏的：
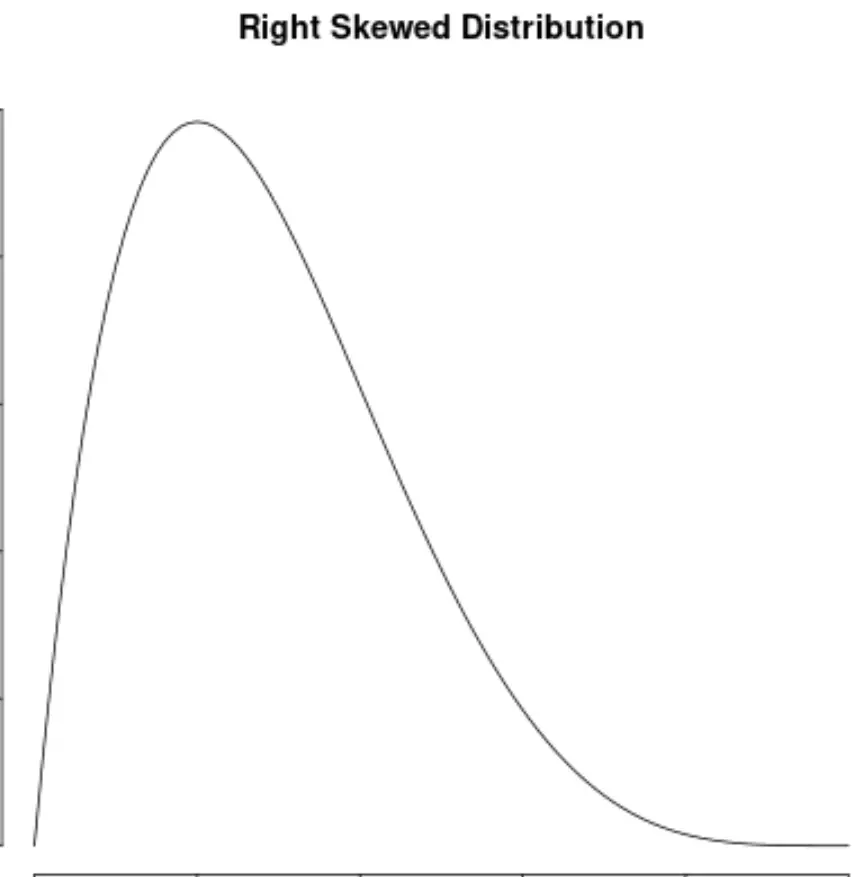
如果分布两边对称，我们就说它没有不对称性：
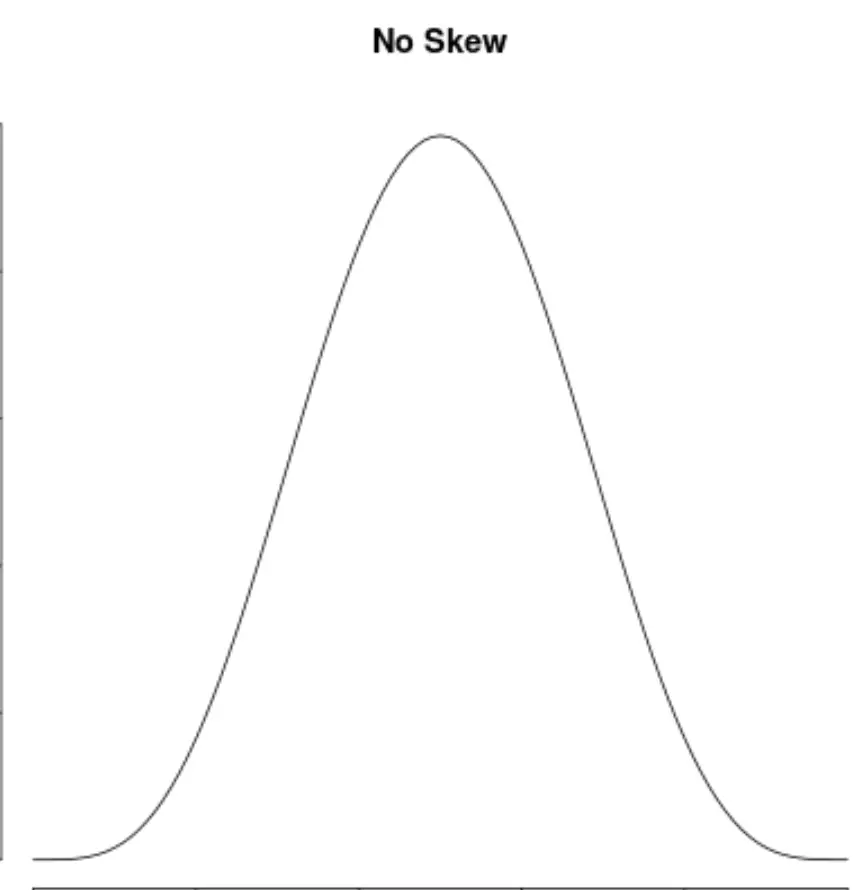
如何解释不对称性
不对称性的值范围可以从负无穷大到正无穷大。
以下是如何解释不对称值：
- 偏度为负值表示尾部位于分布的左侧，并向更多负值延伸。
- 偏度为正值表示尾部位于分布的右侧，并向更正的值延伸。
- 值为零表示分布不存在不对称性，这意味着分布完全对称。
以下示例展示了如何在实践中解释不对称值。
示例 1：左偏分布
大多数人口的死亡年龄分布向左倾斜。大多数人活在70岁到80岁之间，活在这个年龄以下的人越来越少。
如果我们创建一个密度图来可视化死亡年龄值的分布，它可能如下所示：
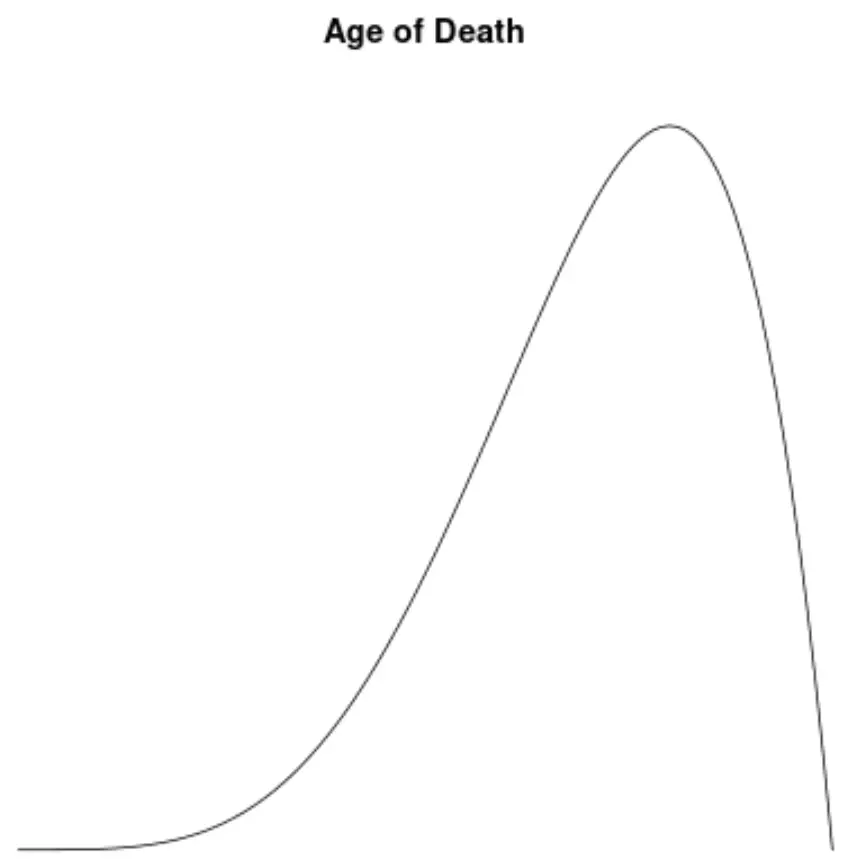
假设我们计算该分布的偏度，发现它是-1.3225 。
由于该值为负数，我们将其解释为分布是左偏的，即尾部向分布的左侧延伸。
示例 2：右偏分布
美国家庭收入的分配向右倾斜，大多数家庭年收入在 30,000 美元到 70,000 美元之间，但右尾较长的家庭收入要高得多。
如果我们创建一个密度图来可视化家庭收入值的分布，它可能如下所示：
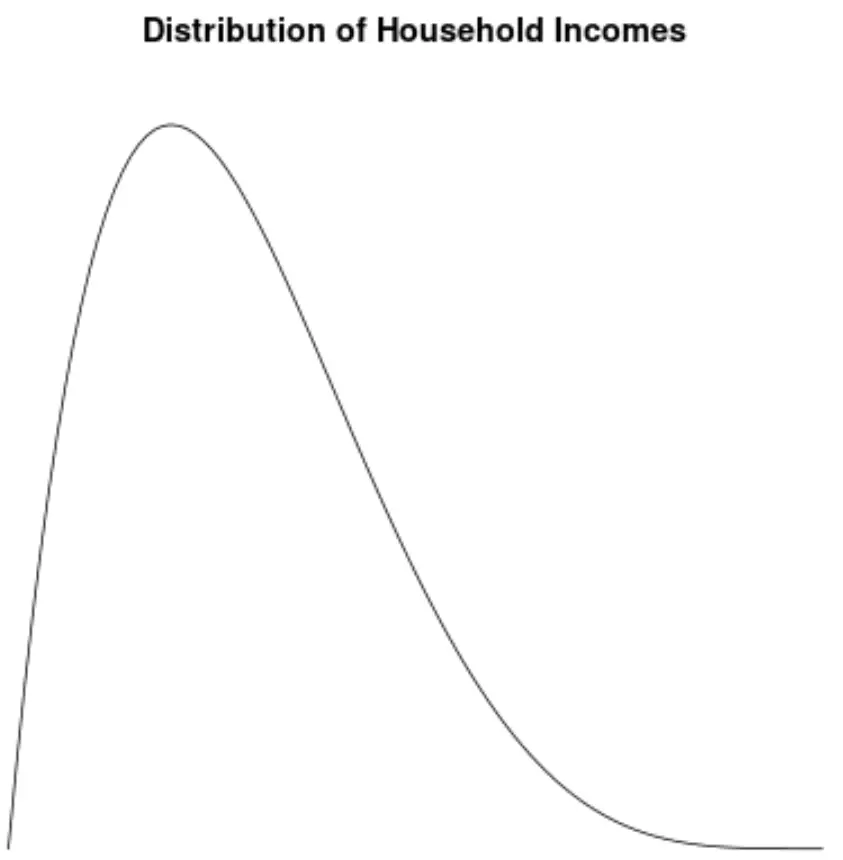
假设我们计算该分布的偏度，发现它是2.0043 。
由于该值为正，我们将其解释为分布是右偏的，即尾部向分布的右侧延伸。
示例 3：无偏见
雄性的体型大致呈正态分布，没有表现出不对称性。例如，美国男性的平均身高约为 69.1 英寸。身高分布大致对称，有的矮有的高。
如果我们创建一个密度图来可视化美国男性身高的分布，它可能如下所示：
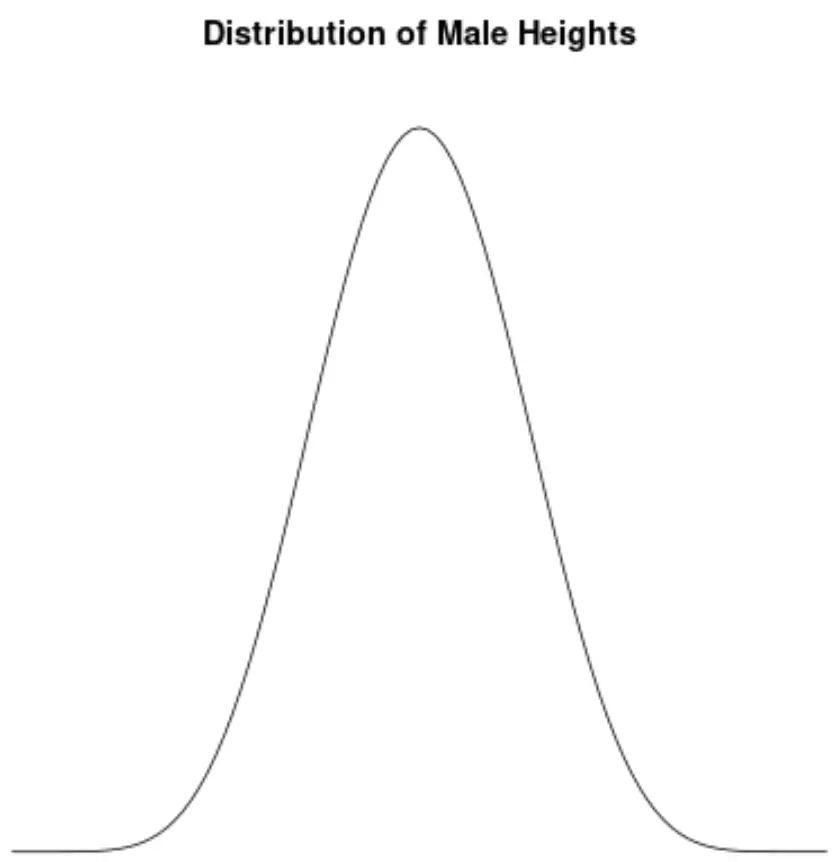
假设我们计算该分布的偏度，发现它是0.0013 。
由于该值接近于零，我们将其解释为分布实际上没有偏斜，这意味着分布两侧的尾部大致相等。
其他资源
以下教程提供了有关倾斜统计数据的其他信息：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多