如何在 stata 中进行双样本 t 检验
双样本 t 检验用于检验两个总体的均值是否相等。
本教程介绍如何在 Stata 中执行两个样本 t 检验。
示例:Stata 中的双样本 t 检验
研究人员想知道新的燃料处理方法是否会导致某辆车的平均英里/加仑发生变化。为了测试这一点,他们进行了一项实验,其中 12 辆汽车接受了新的燃料处理,而 12 辆汽车则没有。
完成以下步骤以执行两个样本 t 检验,以确定这两组之间的平均 mpg 是否存在差异。
第 1 步:加载数据。
首先,通过在命令框中键入use https://www.stata-press.com/data/r13/fuel3并单击 Enter 来加载数据。
步骤2:查看原始数据。
在进行双样本 t 检验之前,我们首先看一下原始数据。从顶部菜单栏中,导航至数据 > 数据编辑器 > 数据编辑器(浏览) 。第一列mpg显示给定汽车的 mpg。第二列对待,表明汽车是否接受了燃料处理(0 = 否,1 = 是)。
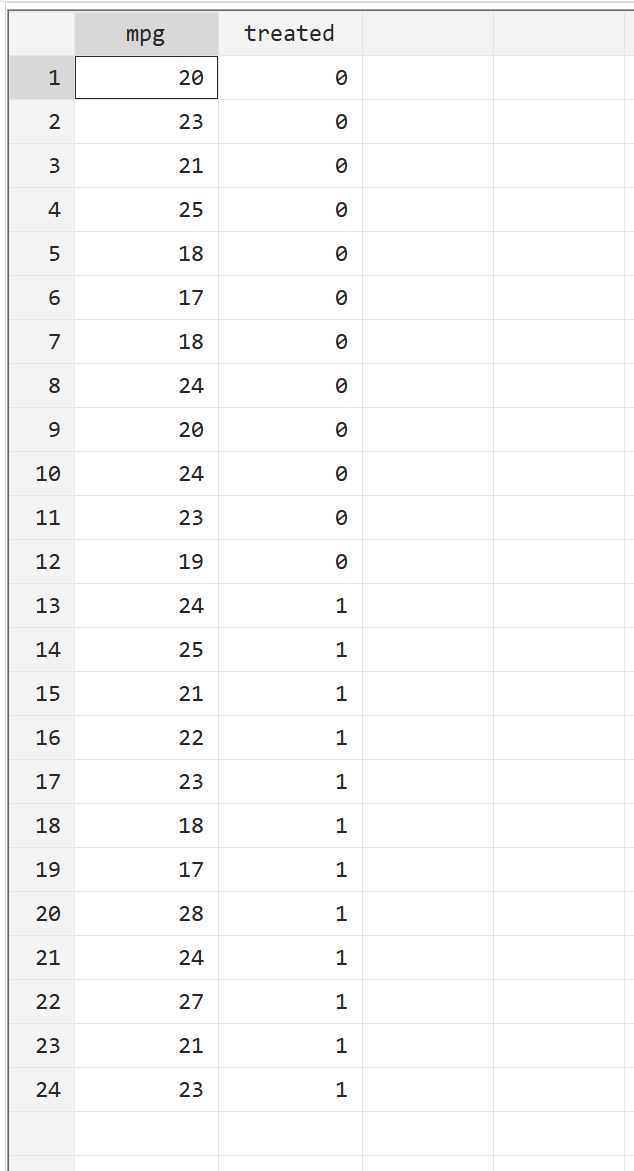
第 3 步:可视化数据。
接下来,让我们可视化数据。我们将创建箱线图来显示每组的 mpg 值的分布。
从顶部菜单栏中,转到图表 > 箱形图。在变量下,选择mpg :
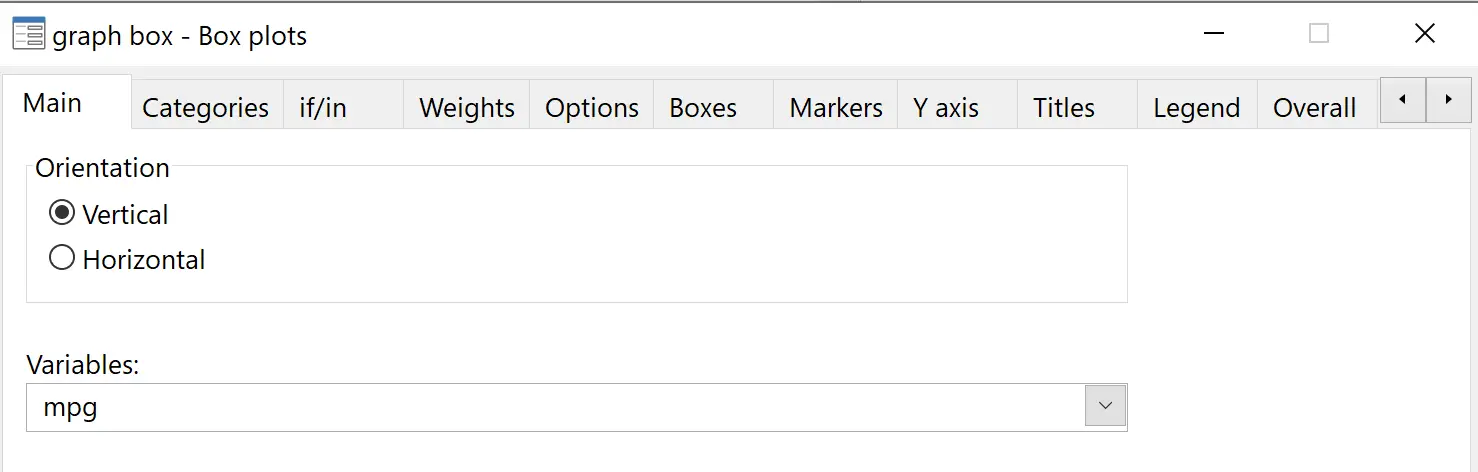
然后,在“分组变量”下的“类别”子标题中,选择“已处理” :
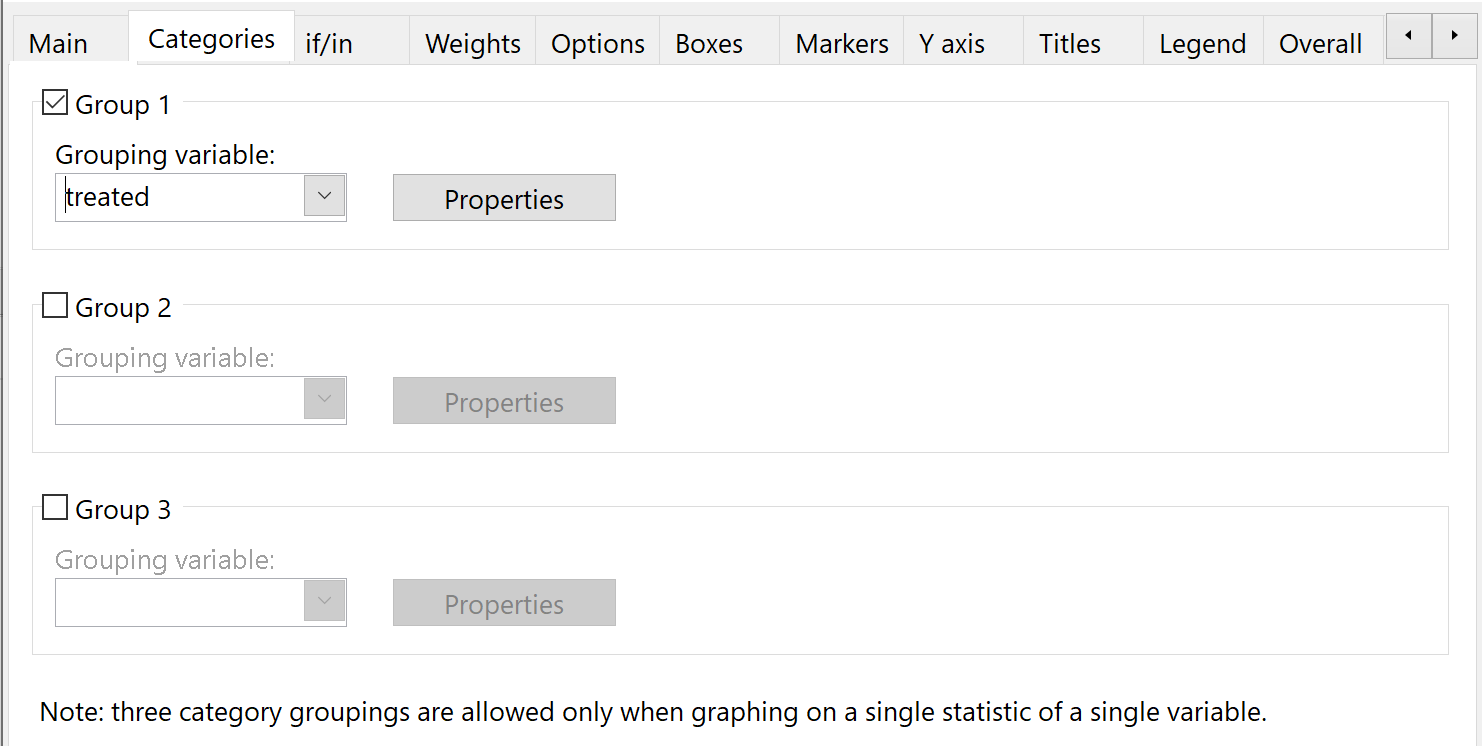
单击“确定” 。将自动显示带有两个箱线图的图表:
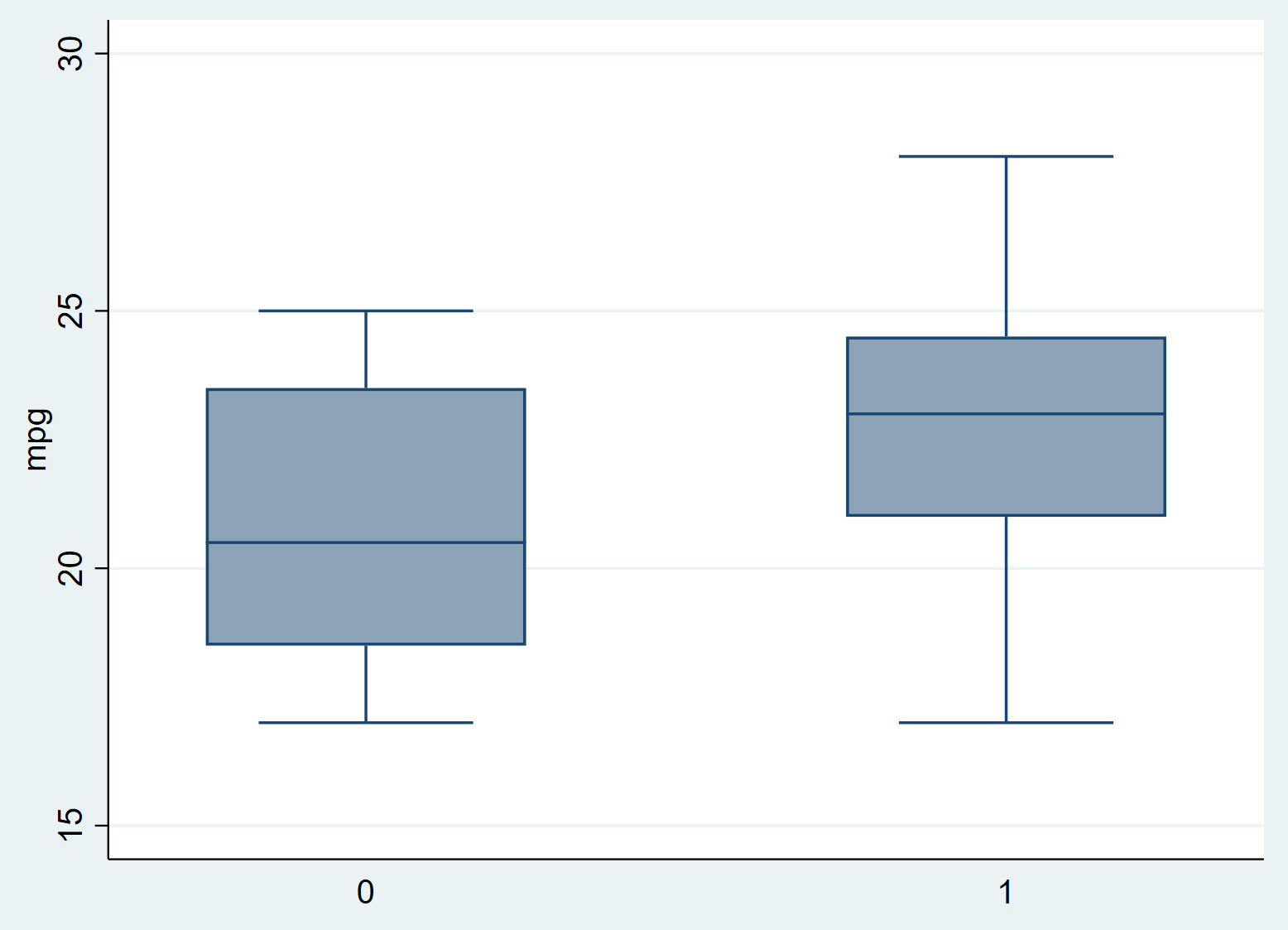
我们可以立即看到,与未治疗组 (0) 相比,治疗组 (1) 的 mpg 似乎更高,但我们需要执行两个样本 t 检验,看看这些差异是否具有统计显着性。 。
步骤 4:执行两个样本 t 检验。
从顶部菜单栏,转到统计 > 摘要、表格和检验 > 经典假设检验 > t 检验(均值比较检验) 。
使用 groups 选择两个样本。对于变量名称,选择mpg 。对于组变量名称,选择Processed 。对于置信级别,选择您想要的级别。值 95 对应显着性水平 0.05。我们将其保留为 95。最后,单击“确定” 。
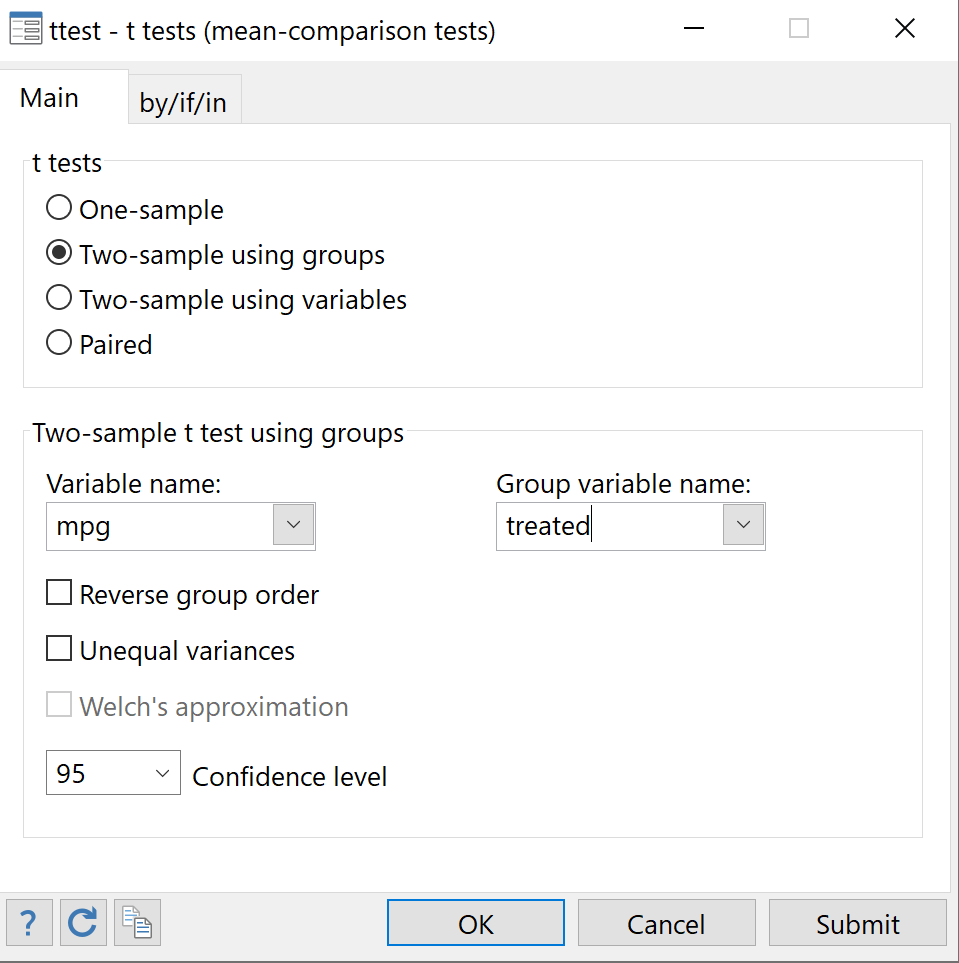
将显示两个样本 t 检验的结果:
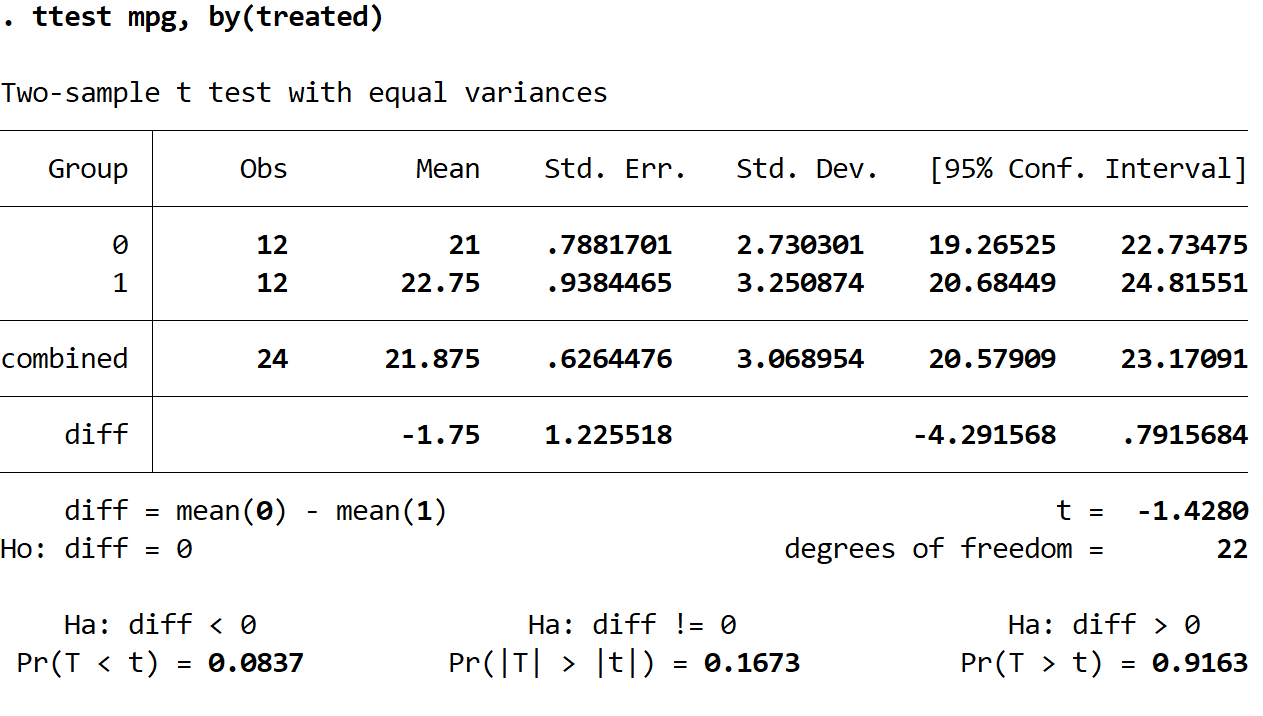
我们收到每个组的以下信息:
观测值:观测值的数量。每组有 12 个观察值。
平均:平均英里/加仑。在第 0 组中,平均值为 21。在第 1 组中,平均值为 22.75。
标准。 Err:标准误差,计算公式为 σ / √ n
标准。 Dev: mpg 的标准偏差。
95% 一致范围:真实群体平均英里数的 95% 置信区间。
t:双样本t检验的检验统计量。
自由度:用于测试的自由度,计算公式为 n-2 = 24-2 = 22。
结果底部显示了三个不同的双样本 t 检验的 p 值。由于我们想要了解两组之间的平均 mpg 是否只是不同,因此我们将查看中间测试的结果(其中备择假设为 Ha:diff !=0),其 p 值为0.1673。 。
由于该值不低于我们的显着性水平 0.05,因此我们无法拒绝原假设。我们没有足够的证据表明两组的真实平均英里数不同。
第五步:报告结果。
最后,我们将报告两个样本 t 检验的结果。以下是如何执行此操作的示例:
对 24 辆汽车进行了两个样本的 T 测试,以确定新的燃油处理是否会导致每加仑平均英里数的差异。每组有 12 辆车。
结果显示,两组之间的平均 mpg没有差异(t = -1.428,df = 22,p = 0.1673),显着性水平为 0.05。
总体平均值的真实差异的 95% 置信区间给出的区间为 (-4.29, 0.79)。