如何在 ti-84 计算器上应用中心极限定理
中心极限定理指出,如果样本量足够大,即使总体分布不正态,样本均值的抽样分布也近似正态。
中心极限定理还指出,抽样分布将具有以下属性:
1.抽样分布的均值将等于总体分布的均值:
x = µ
2.抽样分布的标准差等于总体标准差除以样本量:
s = σ / √n
要在 TI-84 计算器上查找与样本均值相关的概率,我们可以使用带有以下语法的normalcdf()函数:
normalcdf (lower value, upper value, x , s/√ n )
金子:
- x :样本平均值
- s :样本标准差
- n :样本量
要在 TI-84 计算器上访问此功能,只需按2nd ,然后按VARS ,然后滚动到normalcdf(然后按ENTER 。
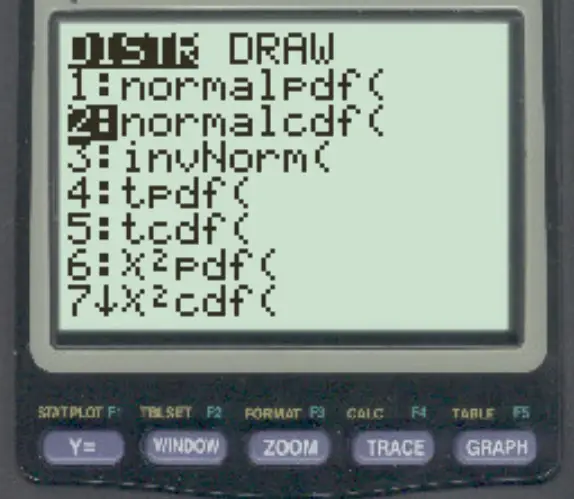
以下示例展示了如何在实践中使用此功能。
示例 1:计算两个值之间的概率
分布的平均值为 70,标准差为 7。如果我们选择大小为 n = 35 的随机样本,请计算样本平均值介于 68 和 72 之间的概率。
我们可以在 TI-84 上使用以下语法:
normalcdf (68, 72, 70, 7/√ 35 )
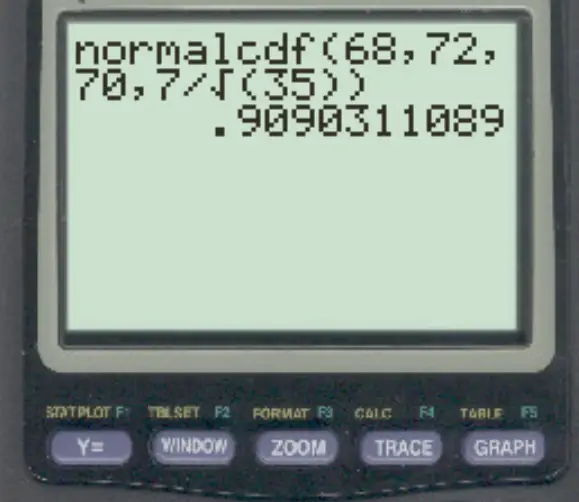
样本均值介于 68 和 72 之间的概率为0.909 。
示例 2:查找大于某个值的概率
分布的平均值为 50,标准差为 4。如果我们选择大小为 n = 30 的随机样本,请找到样本平均值大于 48 的概率。
我们可以在 TI-84 上使用以下语法:
normalcdf (48, E99, 50, 4/√ 30 )
注意:您可以通过按2然后按,按钮访问“E”符号。
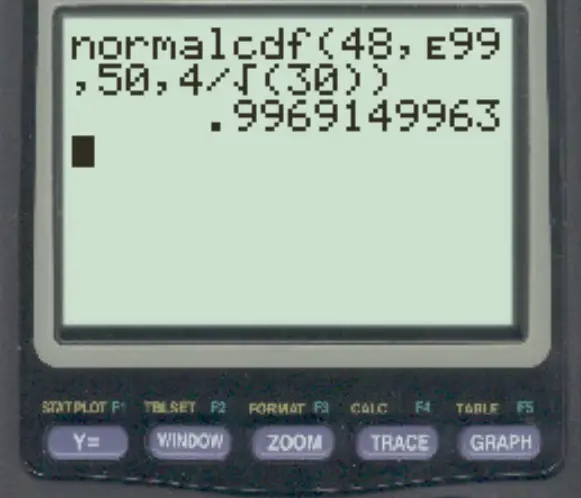
样本均值大于 48 的概率为0.9969 。
示例 3:查找小于某个值的概率
分布的平均值为 20,标准差为 3。如果我们选择大小为 n = 40 的随机样本,请找到样本平均值小于 19 的概率。
我们可以在 TI-84 上使用以下语法:
normalcdf (-E99, 19, 20, 3/√ 40 )
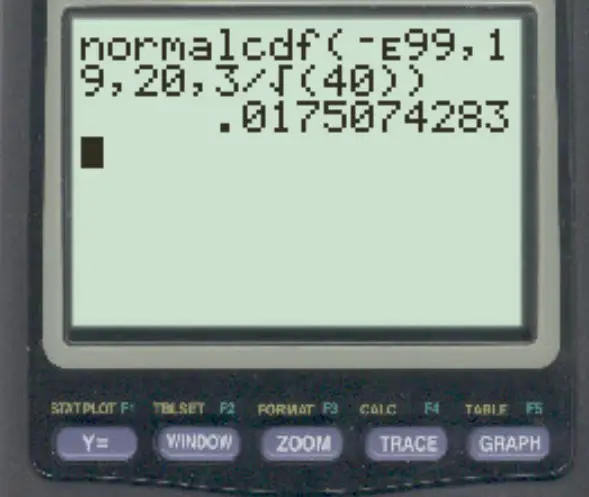
样本均值小于 19 的概率为0.0175 。