如何在 excel 中应用中心极限定理

中心极限定理指出，如果样本量足够大，即使总体分布不正态，样本均值的抽样分布也近似正态。

中心极限定理还指出，抽样分布将具有以下属性：

1.抽样分布的均值将等于总体分布的均值：

x = µ

2.抽样分布的标准差等于总体标准差除以样本量：

s = σ / √n

在本教程中，我们将解释如何将 Excel 中的中心极限定理应用于给定的分布。

在 Excel 中应用中心极限定理

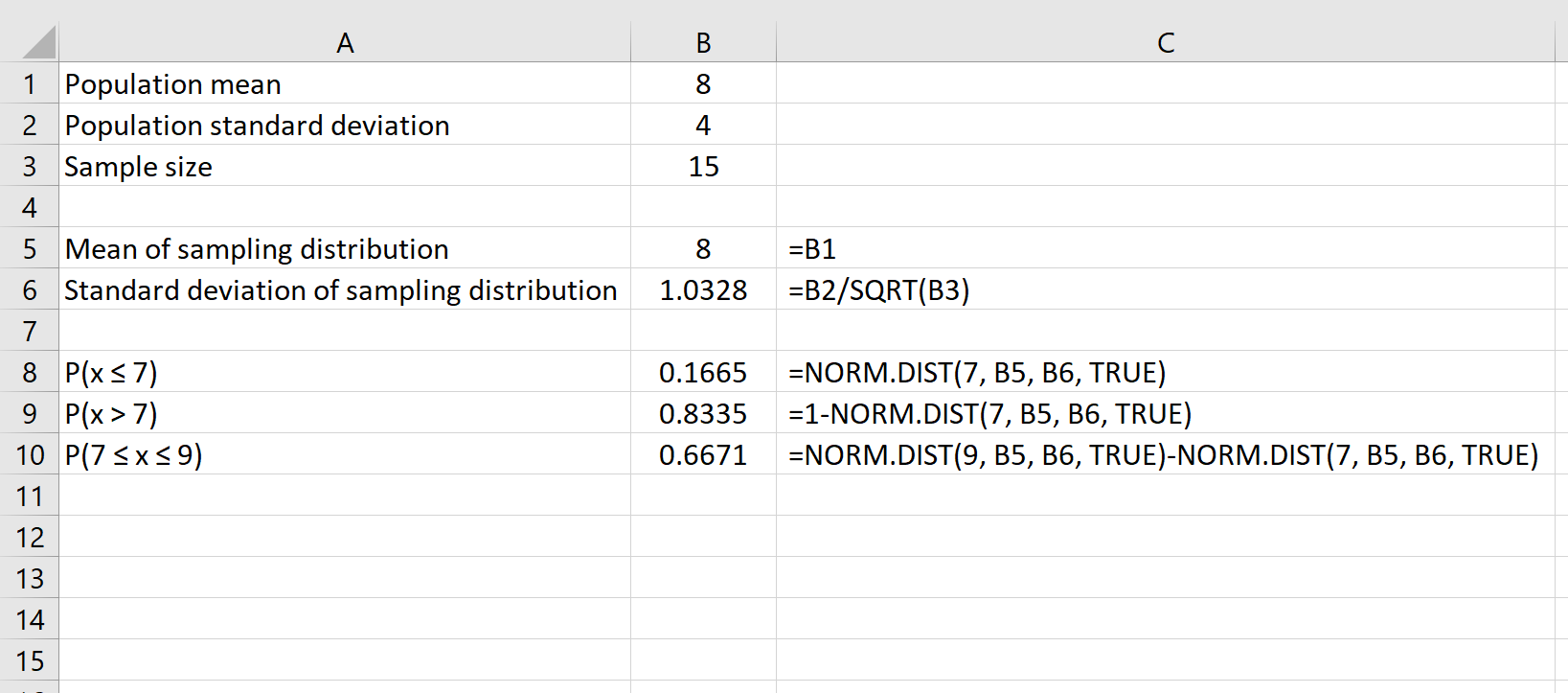
假设我们的分布的平均值为8 ，标准差为4 。我们可以在 Excel 中使用以下公式来查找样本量为15的样本分布的平均值和标准差：

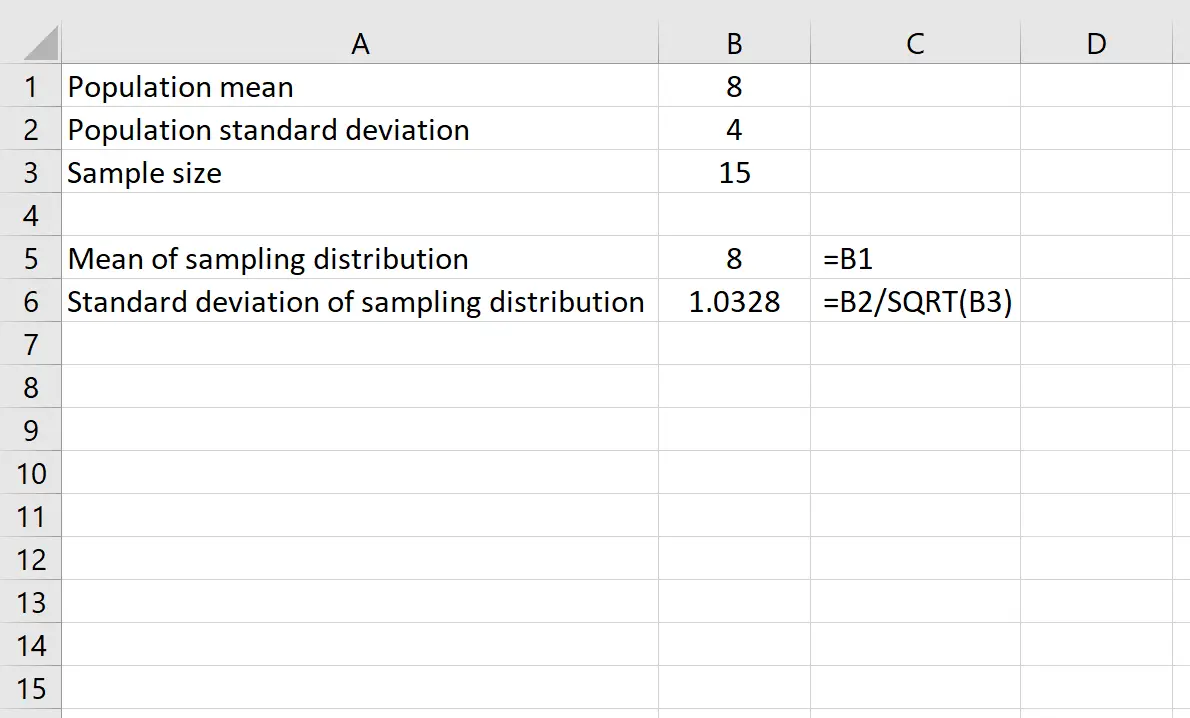
抽样分布的平均值简单地等于总体分布的平均值，即8 。

抽样分布的标准差等于总体标准差除以样本量，即： 4 /√15 = 1.0328 。

我们还可以使用中心极限定理来回答有关概率的问题。例如，如果给定总体的平均值为8 ，标准差为4 ，则给定大小为15的样本的概率是多少 平均值小于或等于7 ？

为了回答这个问题，我们可以使用Excel中的NORM.DIST()函数，它使用以下语法：

NORM.DIST(x, 平均值, standard_dev, 累积)

金子：

• x： sample 表示要测试
• 平均值：抽样分布的预期平均值
• standard_dev：抽样分布的预期标准差
• cumulative: TRUE 返回正常的 CDF 值； FALSE 返回普通 PDF 的值。在我们的例子中，我们将始终使用 TRUE。

该函数将返回样本均值小于或等于某个值的概率。

这是我们在本例中使用的公式：

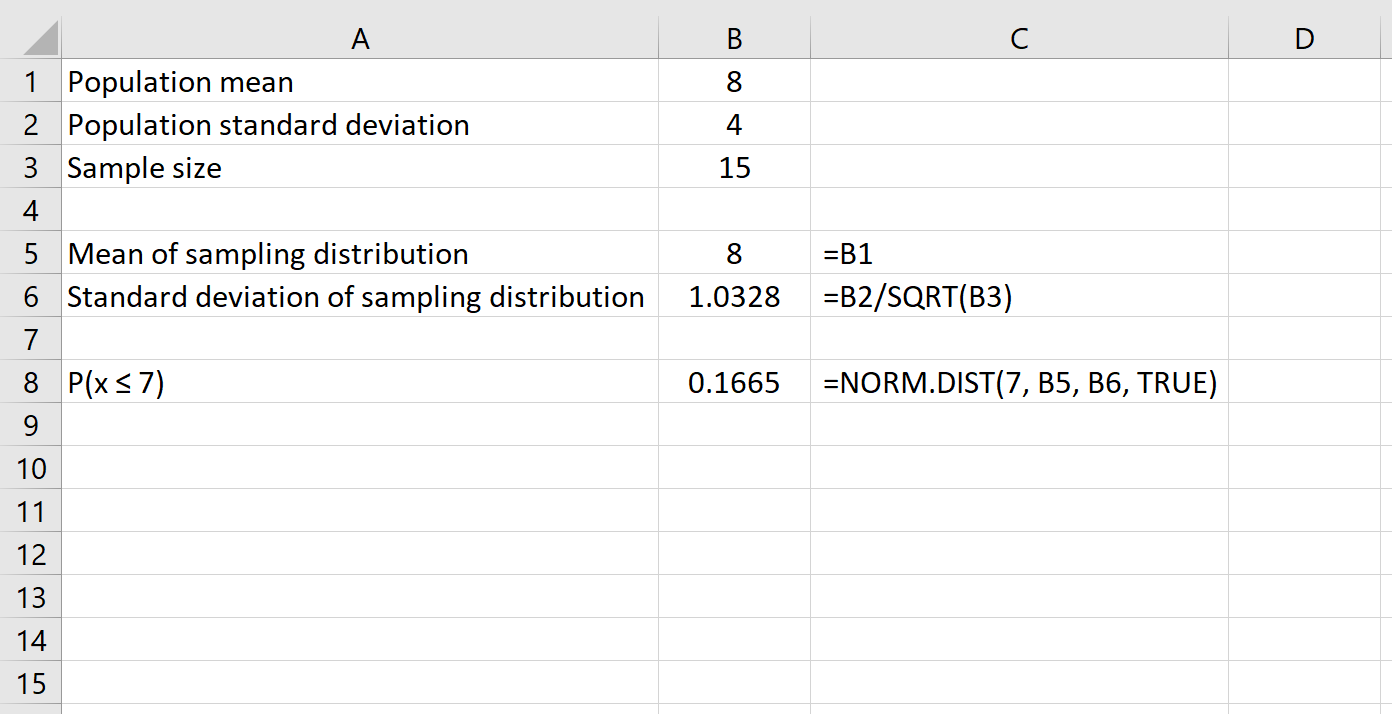
这告诉我们，对于平均值为8且标准差为4 的总体，给定大小为 15的样本的概率 平均值小于或等于7或0.1665 。

我们还可以通过简单地使用公式1 – NORM.DIST()来找到给定样本量的均值大于某个数字的概率。

例如，以下公式显示如何确定给定样本量 15 的均值大于7 的概率：

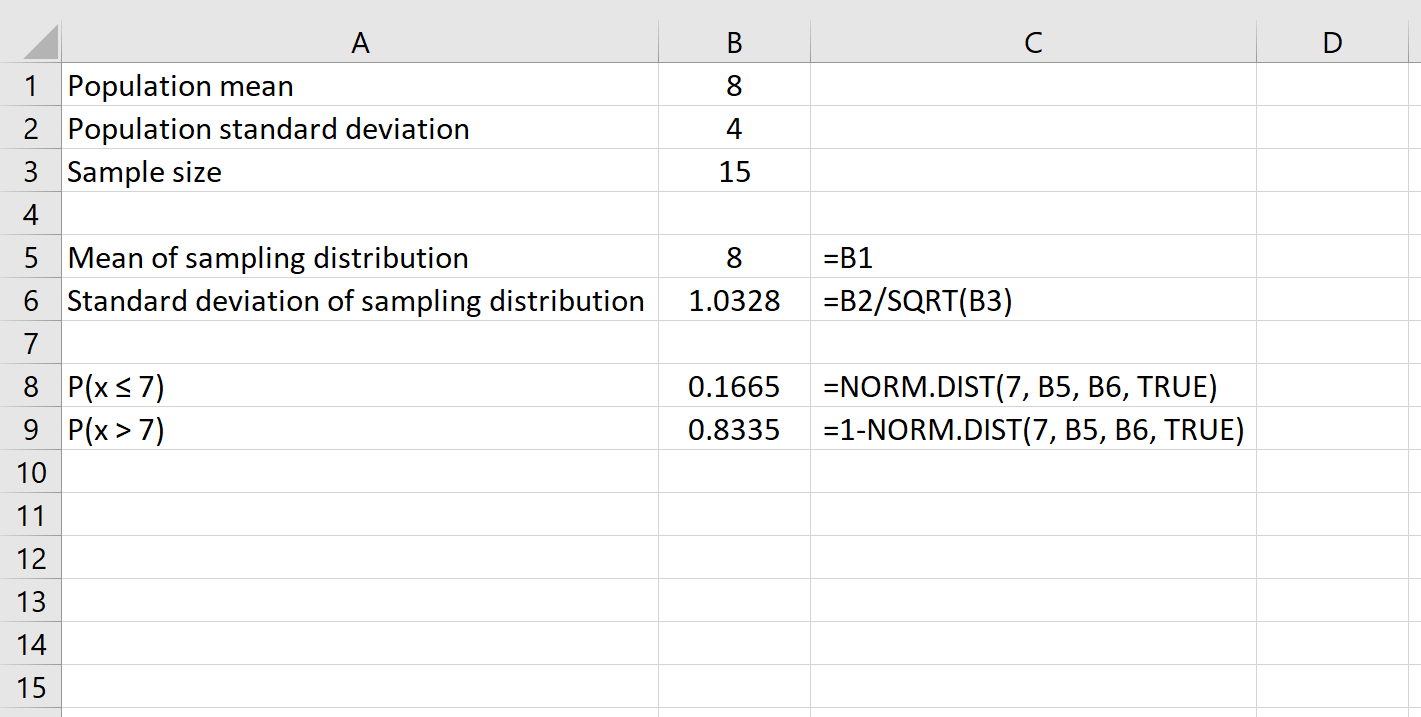
最后，我们可以使用公式NORM.DIST(larger number) – NORM.DIST(smaller number)找到给定样本量在两个数字之间具有平均值的概率。

例如，以下公式显示如何查找给定样本量 15 的均值在 7 到 9 之间的概率：

其他资源

中心极限定理计算器
如何在 Excel 中应用经验法则
如何在 Excel 中创建钟形曲线