为什么统计数据很重要？ （统计数据如此重要的 10 个理由！）
统计学领域涉及数据的收集、分析、解释和呈现。
随着技术越来越多地出现在我们的日常生活中，产生和收集的数据比人类历史上以往任何时候都多。
统计领域可以帮助我们了解如何使用这些数据来执行以下任务：
- 更好地了解我们周围的世界。
- 使用数据做出决策。
- 使用数据对未来进行预测。
在本文中，我们分享了统计领域在现代生活中如此重要的 10 个原因。
理由一：使用描述性统计来了解世界
描述性统计用于描述一段原始数据。描述性统计主要分为三种类型：
- 统计汇总
- 图形
- 桌子
这些元素中的每一个都可以帮助我们更好地理解现有数据。
例如，假设我们有一个原始数据集，显示某个城市 10,000 名学生的考试成绩。我们可以使用描述性统计来：
- 计算平均测试成绩和测试结果的标准差。
- 生成直方图或箱线图以可视化测试结果的分布。
- 创建频率表以了解测试结果的分布。
通过使用描述性统计，我们可以比仅仅查看原始数据更容易地了解学生的考试成绩。
原因 2：谨防误导性图形
越来越多的图形出现在期刊、媒体、在线文章和杂志中。不幸的是，如果您不了解基础数据，图表通常可能会产生误导。
例如，假设某期刊发表了一项研究，发现某所大学学生的 GPA 和 ACT 分数之间呈负相关。
然而，这种负相关的发生只是因为 GPA 和 ACT 分数都高的学生能够进入精英大学，而 GPA 和 ACT 分数都低的学生根本不会被录取。
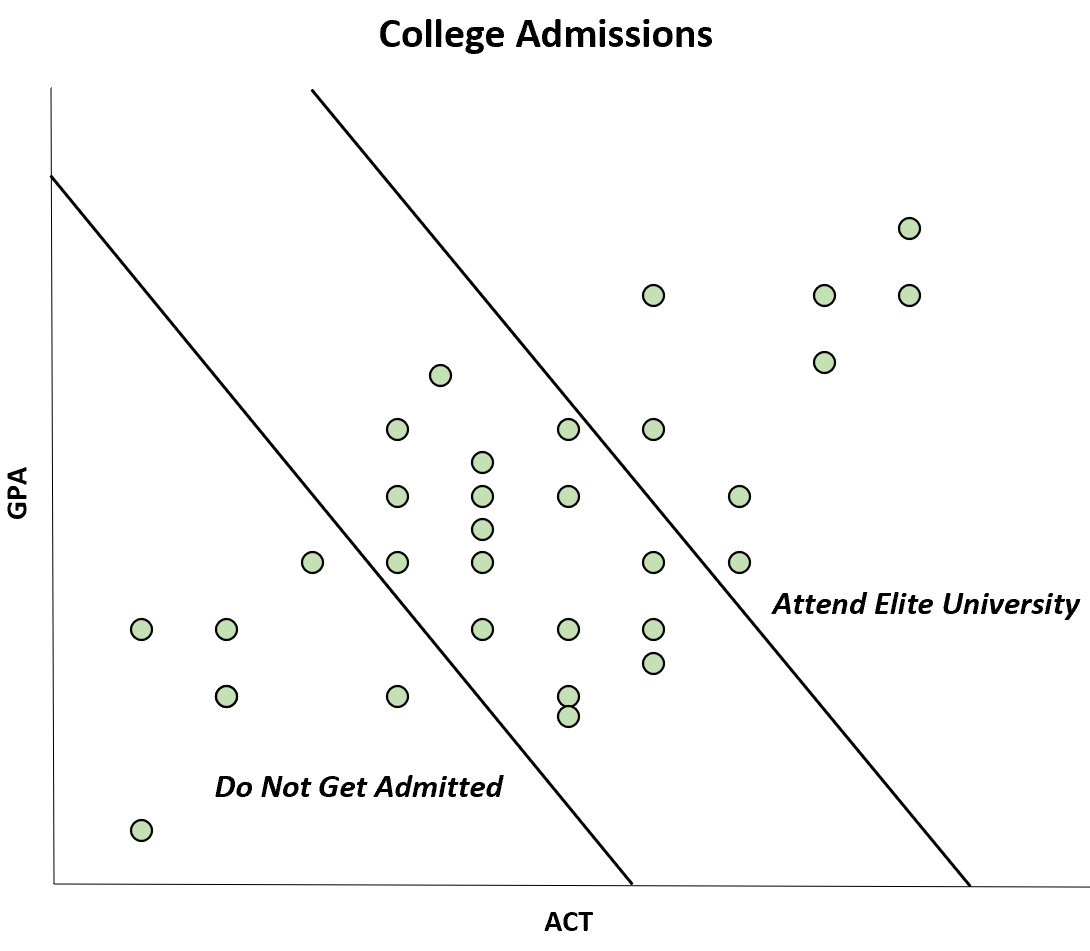
尽管 ACT 和 GPA 之间的相关性在总体中呈正相关，但在样本中却呈负相关。
这种特殊的偏差被称为伯克森偏差。通过意识到这种偏见，您可以避免被某些图表误导。
原因三：警惕容易混淆的变量
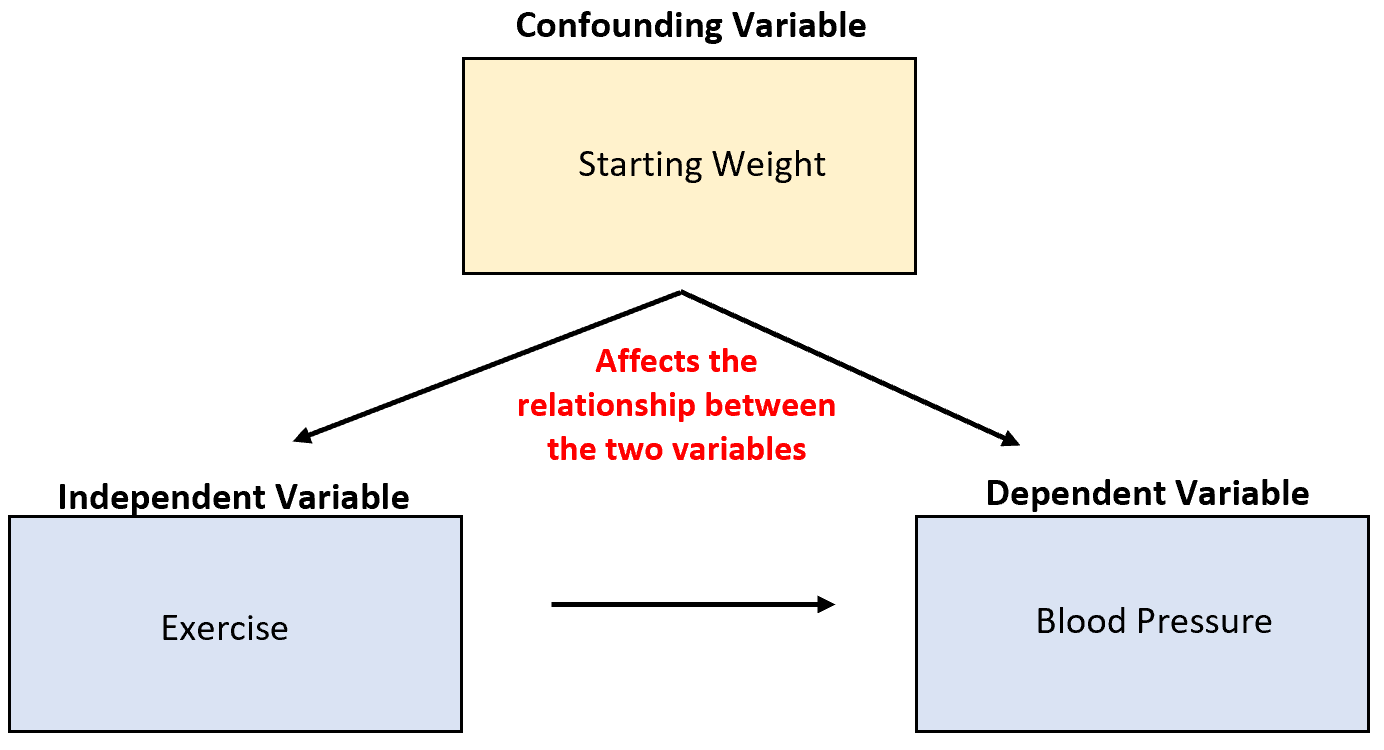
您将在统计学中学到的一个重要概念是混淆变量的概念。
这些变量未被考虑在内，可能会混淆实验结果并导致不可靠的结论。
例如，假设研究人员收集了有关冰淇淋销售和鲨鱼袭击的数据，并发现这两个变量高度相关。这是否意味着冰淇淋销量的增加导致了更多的鲨鱼袭击？
这不太可能。最可能的原因是令人困惑的温度变化。当外面变暖时，更多的人购买冰淇淋，更多的人去海边。
原因 4：利用概率做出更好的决策
统计学最重要的子领域之一是概率。它是研究事件发生概率的领域。
通过对概率有基本的了解，您可以在现实世界中做出更明智的决策。
例如，假设一名高中生知道他有 10% 的机会被某所大学录取。使用通过“至少一所”的概率公式，该学生可以找到他将被他申请的至少一所大学录取的概率，并可以根据结果调整他申请的大学数量。
原因 5：了解研究中的 P 值
您将在统计学中学到的另一个重要概念是p 值。
p 值的经典定义是：
p 值是在原假设成立的情况下观察到至少与样本统计量一样极端的样本统计量的概率。
例如，假设一家工厂声称生产平均重量为 200 磅的轮胎。审核员假设该工厂生产的轮胎的实际平均重量相差 200 磅。因此，他进行了假设检验，发现检验的 p 值为 0.04。
以下是如何解释此 p 值：
如果工厂实际生产平均重量为 200 磅的轮胎，那么由于随机抽样误差，所有审核中将有 4% 或更多达到样本中观察到的效果。这告诉我们，如果工厂实际生产平均重量为200磅的轮胎，那么获得审核员获得的样本数据将是相当罕见的。
因此，审核员可能会拒绝原假设，即该工厂生产的轮胎的实际平均重量确实为 200 磅。
原因六：了解相关性
您将在统计学中学到的另一个重要概念是相关性，它告诉我们两个变量之间的线性关联。
相关系数的值始终介于 -1 和 1 之间，其中：
- -1 表示两个变量之间完全负线性相关
- 0 表示两个变量之间不存在线性相关
- 1 表示两个变量之间存在完全正线性相关
通过了解这些值，您可以了解现实世界中变量之间的关系。
例如，如果广告支出和收入之间的相关性为 0.87，那么您可以理解这两个变量之间存在很强的正相关关系。当您在广告上花费更多的钱时，您可以预期收入会增加。
理由七：对未来做出预测
学习统计学的另一个重要原因是了解基本的回归模型，例如：
每个模型都允许您根据模型中某些预测变量的值来预测响应变量的未来值。
例如，公司在使用年龄、收入、种族等预测变量时，一直在现实世界中使用多重线性回归模型。预测有多少顾客会在他们的商店消费。
同样，物流公司使用总需求、人口规模等预测变量。来预测未来的销售情况。
无论您从事哪个领域，回归模型都有很好的机会用于预测未来的现象。
原因 8：了解研究中潜在的偏见
研究统计学的另一个原因是要意识到现实世界研究中可能出现的所有不同类型的偏差。
这里有些例子：
通过对这些类型的偏见有基本的了解，您可以在进行研究时避免犯下这些偏见，或者在阅读其他研究论文或研究时意识到它们。
原因 9：了解统计测试所做的假设
许多统计测试对所研究的基础数据做出假设。
在阅读研究结果甚至进行自己的研究时，重要的是要了解需要做出哪些假设才能使结果可靠。
以下文章分享了许多常用统计测试和程序中所做的假设：
原因10：避免过度概括
研究统计学的另一个原因是理解过度概括的概念。
当参与研究的个体不能代表总体人群中的个体时，就会发生这种情况，因此将研究结果推广到整个人群是不合适的。
例如，假设我们想知道某所学校有多少学生喜欢“戏剧”作为他们最喜欢的电影类型。如果学生总人数由 50% 的男孩和 50% 的女孩混合，那么如果选择戏剧作为最喜欢的类型的男孩明显减少，那么由 90% 的男孩和 10% 的女孩组成的样本可能会导致有偏差的结果。
理想情况下，我们希望我们的样本类似于我们总体的“迷你版”。因此，如果整个学生人口由 50% 的女孩和 50% 的男孩组成，那么如果我们的样本包含 90% 的男孩和仅 10% 的女孩，则该样本将不具有代表性。
因此，无论您是进行自己的调查还是阅读调查结果，重要的是要了解样本数据是否代表总人口以及调查结果是否可以自信地推广到总体。
其他资源
查看以下文章，以基本了解介绍性统计中最重要的概念：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多