如何在 python 中执行二次回归

二次回归是一种回归类型，当真实关系是二次关系（在图表上可能看起来像“U”或倒“U”）时，我们可以用它来量化预测变量和响应变量之间的关系。

也就是说，随着预测变量的增加，响应变量也趋于增加，但在某一点之后，随着预测变量继续增加，响应变量开始减少。

本教程介绍如何在 Python 中执行二次回归。

示例：Python 中的二次回归

假设我们有 16 个不同的人每周工作时数和报告的幸福程度（范围为 0 到 100）的数据：

 import numpy as np
import scipy.stats as stats

#define variables
hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60]
happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]

如果我们对这些数据做一个简单的散点图，我们可以看到两个变量之间的关系是“U”形的：

 import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(hours, happ) 

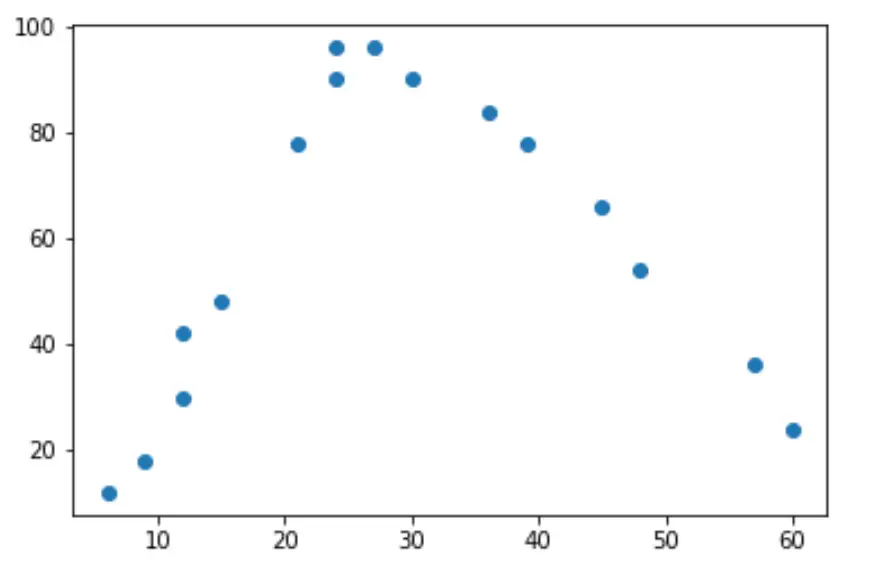
随着工作时间的增加，幸福感也会增加，但一旦每周工作时间超过约 35 小时，幸福感就开始下降。

由于这种“U”形状，这意味着二次回归可能是量化两个变量之间关系的良好候选者。

要实际执行二次回归，我们可以使用numpy.polyfit()函数拟合次数为 2 的多项式回归模型：

 import numpy as np

#polynomial fit with degree = 2
model = np.poly1d(np.polyfit(hours, happ, 2))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(hours, happ)
plt.plot(polyline, model(polyline))
plt.show() 

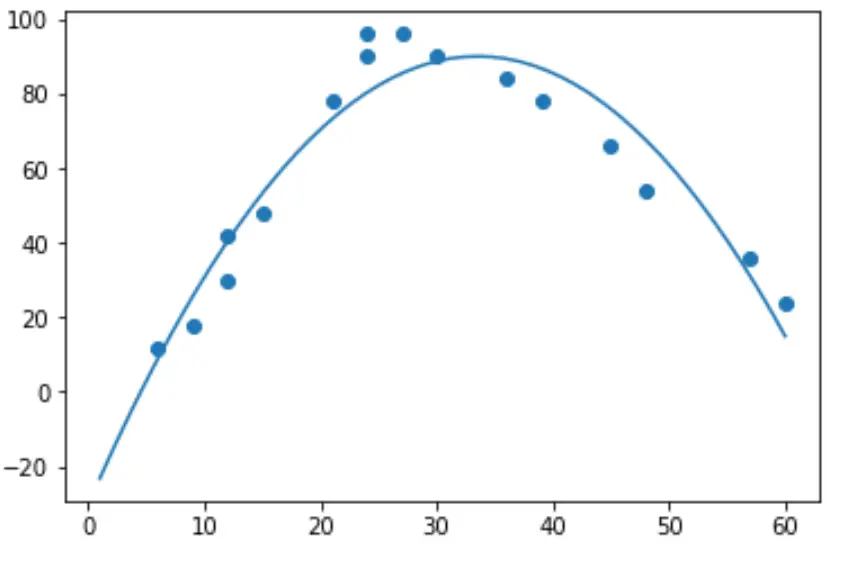
我们可以通过打印模型系数得到拟合的多项式回归方程：

 print (model)

-0.107x 2 + 7.173x - 30.25

拟合的二次回归方程为：

幸福 = -0.107(小时) ² + 7.173(小时) – 30.25

我们可以使用这个方程根据个人的工作时间来计算他们的预期幸福水平。例如，每周工作 30 小时的人的预期幸福水平是：

幸福 = -0.107(30) ² + 7.173(30) – 30.25 = 88.64 。

我们还可以编写一个简短的函数来获取模型的 R 平方，它是响应变量中可以由预测变量解释的方差的比例。

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(hours, happ, 2)

{'r_squared': 0.9092114182131691}

在此示例中，模型的 R 方为0.9092 。

这意味着报告的幸福水平的 90.92% 的变化可以通过预测变量来解释。

其他资源

如何在 Python 中执行多项式回归
如何在 R 中执行二次回归
如何在 Excel 中执行二次回归