如何在 stata 中进行二次回归

当两个变量具有线性关系时，通常可以使用简单线性回归来量化它们的关系。

但是，当两个变量具有二次关系时，可以使用二次回归来量化它们的关系。

本教程介绍如何在 Stata 中执行二次回归。

示例：Stata 中的二次回归

假设我们想了解工作时间与幸福感之间的关系。我们有以下关于 16 名不同的人每周工作时数和报告的幸福程度（范围为 0 到 100）的数据：

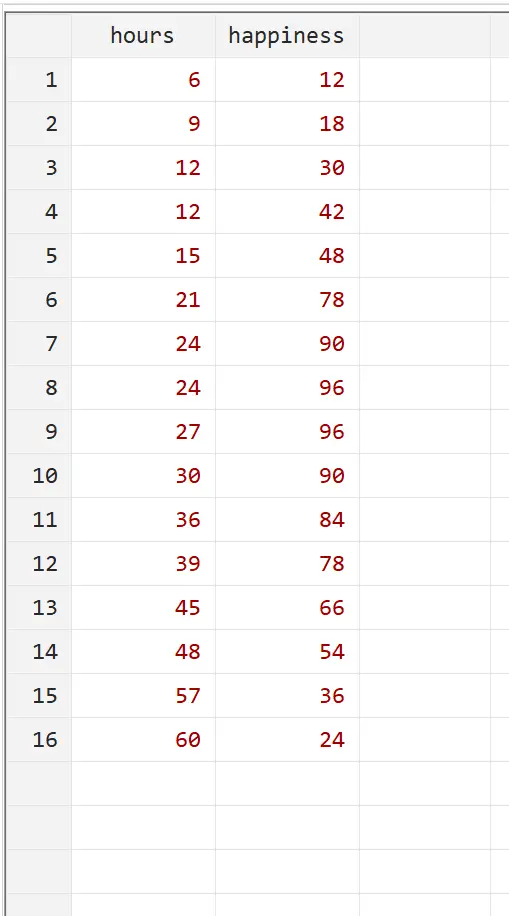
您可以通过使用顶部菜单中的“数据”>“数据编辑器”>“数据编辑器（编辑）”将确切的数据输入到 Stata 中来重现此示例。

使用以下步骤在 Stata 中执行二次回归。

步骤 1：可视化数据。

在使用二次回归之前，我们必须确保解释变量（小时）和响应变量（幸福）之间的关系确实是二次关系。因此，让我们通过在命令框中键入以下内容，使用散点图可视化数据：

驱散幸福的时光

这会产生以下散点图：

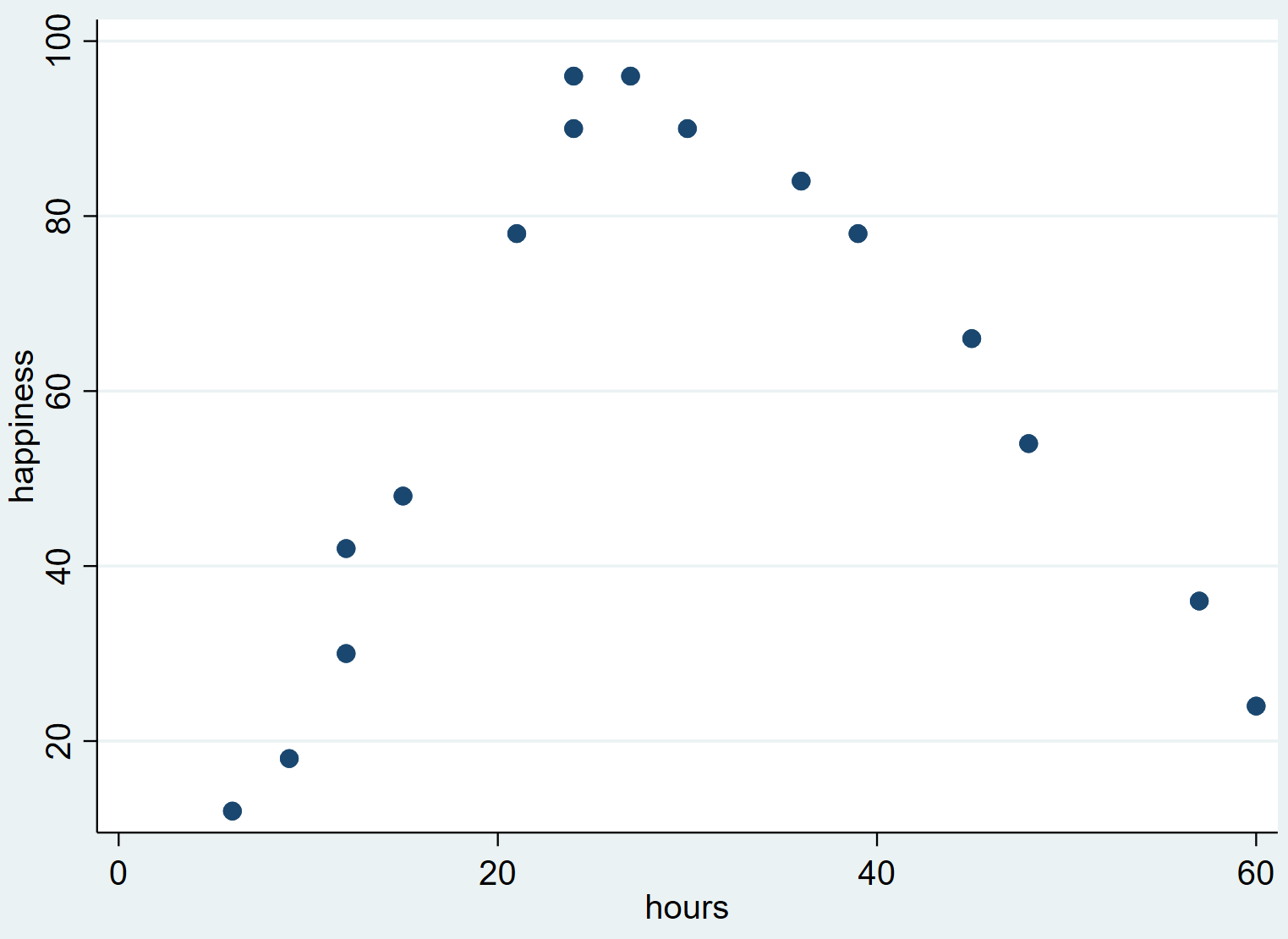
我们可以看到，随着工作时间从零增加到某个点，幸福感往往会增加，但随着工作时间超过 30 小时左右，幸福感开始下降。

散点图中的倒“U”形表明工作时间和幸福感之间存在二次关系，这意味着我们应该使用二次回归来量化这种关系。

步骤 2：执行二次回归。

在将二次回归模型拟合到数据之前，我们需要为小时预测变量的平方值创建一个新变量。我们可以通过在命令框中键入以下内容来完成此操作：

发电小时2 = 小时*小时

我们可以通过从顶部菜单转到数据>数据编辑器>数据编辑器（浏览）来查看这个新变量。

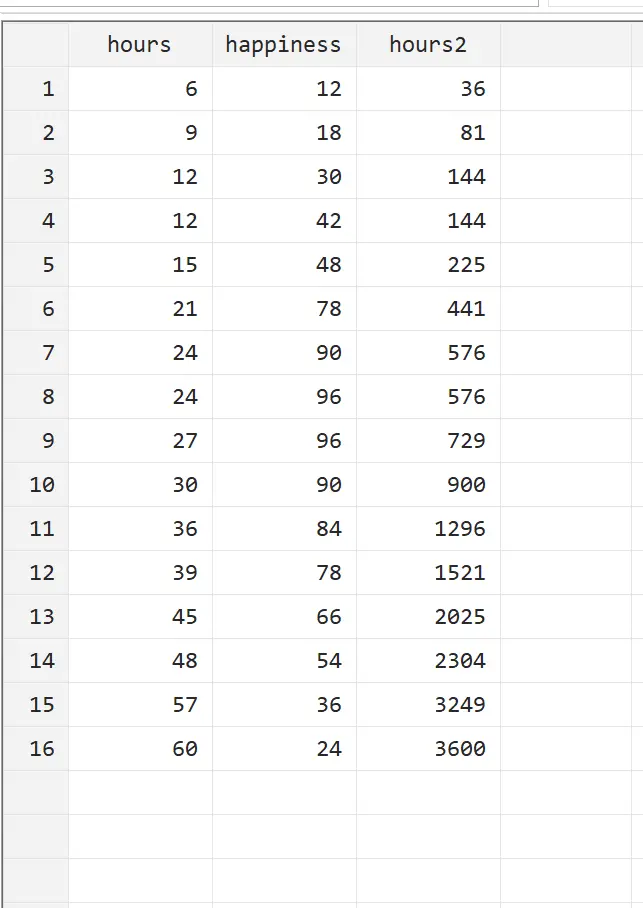
我们可以看到，hours2 就是小时的平方。现在，我们可以使用“小时”和“小时2”作为解释变量，使用“幸福感”作为响应变量来执行二次回归。要执行二次回归，请在命令框中键入以下内容：

幸福时间的回归时间2

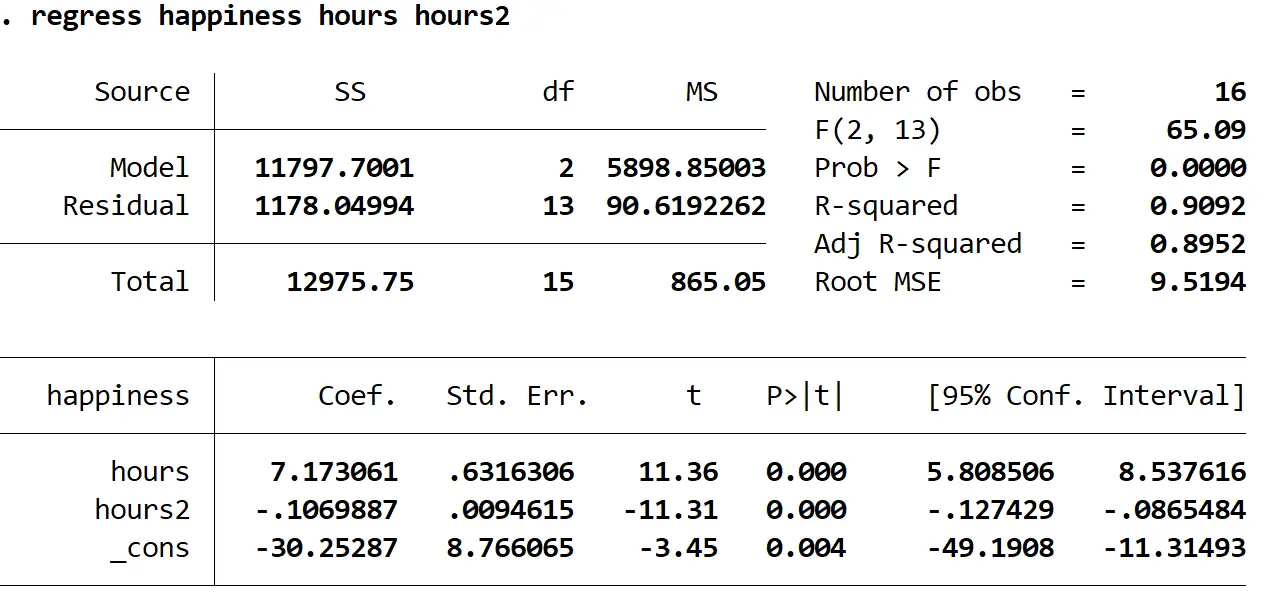
以下是如何解释结果中最有趣的数字：

概率 > F： 0.000。这是整体回归的 p 值。由于该值小于 0.05，这意味着预测变量hours和hours ²组合与响应变量happy具有统计显着关系。

R 平方： 0.9092。这是可以由解释变量解释的响应变量方差的比例。在这个例子中，90.92% 的幸福感变化可以用小时和小时²来解释。

回归方程：我们可以使用输出表中显示的系数值形成回归方程。在这种情况下，方程为：

预测幸福 = -30.25287 + 7.173061（小时）– 0.1069887（ ²小时）

我们可以使用这个方程来计算一个人在每周工作时数的情况下的预期幸福感。

例如，一个每周工作 60 小时的人的幸福指数应该为 14.97：

预测幸福 = -30.25287 + 7.173061(60) – .1069887(60 ² ) = 14.97 。

相反，每周工作 30 小时的人的幸福指数应该为 88.65：

预测幸福 = -30.25287 + 7.173061(30) – .1069887(30 ² ) = 88.65 。

第三步：报告结果。

最后，我们想要报告二次回归的结果。以下是如何执行此操作的示例：

进行二次回归来量化个人工作小时数与其相应幸福水平（从 0 到 100 衡量）之间的关系。分析中使用了 16 人的样本。

结果表明，解释变量“小时”和“小时² ”与响应变量幸福感之间存在统计显着关系（F(2, 13) = 65.09，p < 0.0001）。

这两个解释变量合计占幸福感解释变异的 90.92%。

回归方程为：

预测幸福 = -30.25287 + 7.173061（小时）– 0.1069887（ ²小时）