如何在 google 表格中使用二项式分布
统计学中的二项式分布描述了当单个实验成功的概率为p时,在n次试验中获得k次成功的概率。
要计算 Google Sheets 中的二项式分布概率,我们可以使用BINOMDIST函数,该函数使用以下基本语法:
BINOMDIST(k, n, p, 累积)
金子:
- k : 成功次数
- n :尝试次数
- p :给定测试的成功概率
- cumulative :是否计算累积概率(默认值为FALSE)
以下示例展示了如何在实践中使用此功能。
示例 1:正好 k 次成功的概率
Ty 的罚球命中率为 60%。如果他罚球 12 次,他罚中 10 次的概率是多少?
为了回答这个问题,我们可以在Google表格中使用以下公式:
= BINOMDIST ( 10,12,0.6 , FALSE ) _ _ _ _
以下屏幕截图显示了如何在实践中使用该公式:
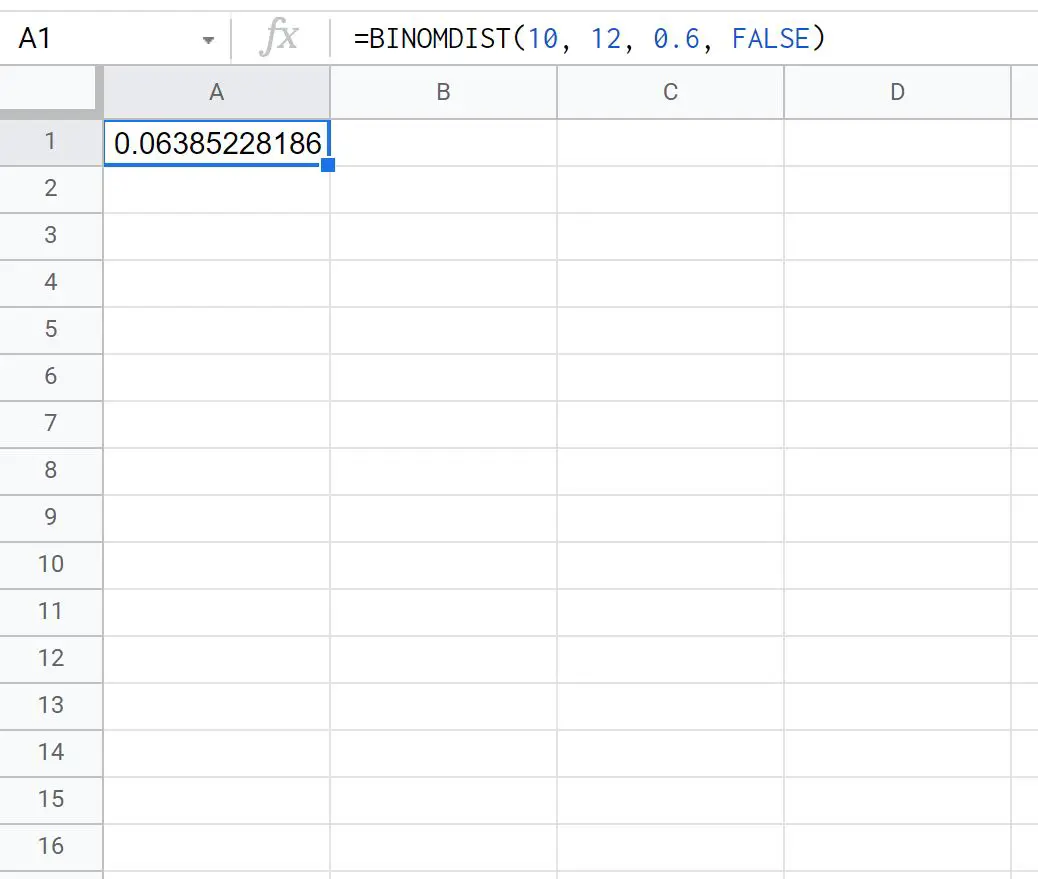
Ty 在 12 次罚球中准确命中 10 次的概率是0.0639 。
示例 2:成功概率小于 k
Ty 的罚球命中率为 60%。如果他罚球 12 次,那么他罚球少于 10 次的概率是多少?
为了回答这个问题,我们可以在Google表格中使用以下公式:
= BINOMDIST ( 9,12,0.6 , TRUE ) _ _ _ _
以下屏幕截图显示了如何在实践中使用该公式:
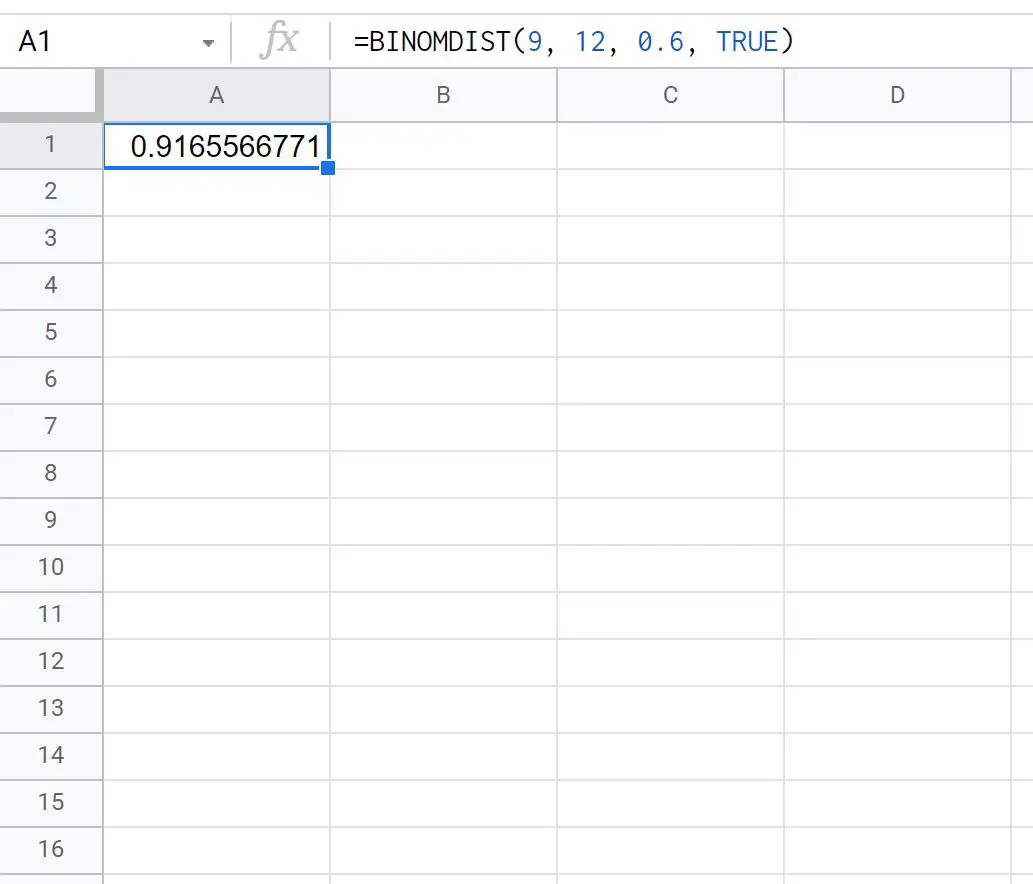
Ty 12 次罚球中少于 10 次的概率是0.9166 。
示例 3:小于或等于 k 成功的概率
Ty 的罚球命中率为 60%。如果他罚球 12 次,那么他罚球次数小于或等于 10 次的概率是多少?
为了回答这个问题,我们可以在Google表格中使用以下公式:
= BINOMDIST ( 10,12,0.6 , TRUE ) _ _ _ _
以下屏幕截图显示了如何在实践中使用该公式:
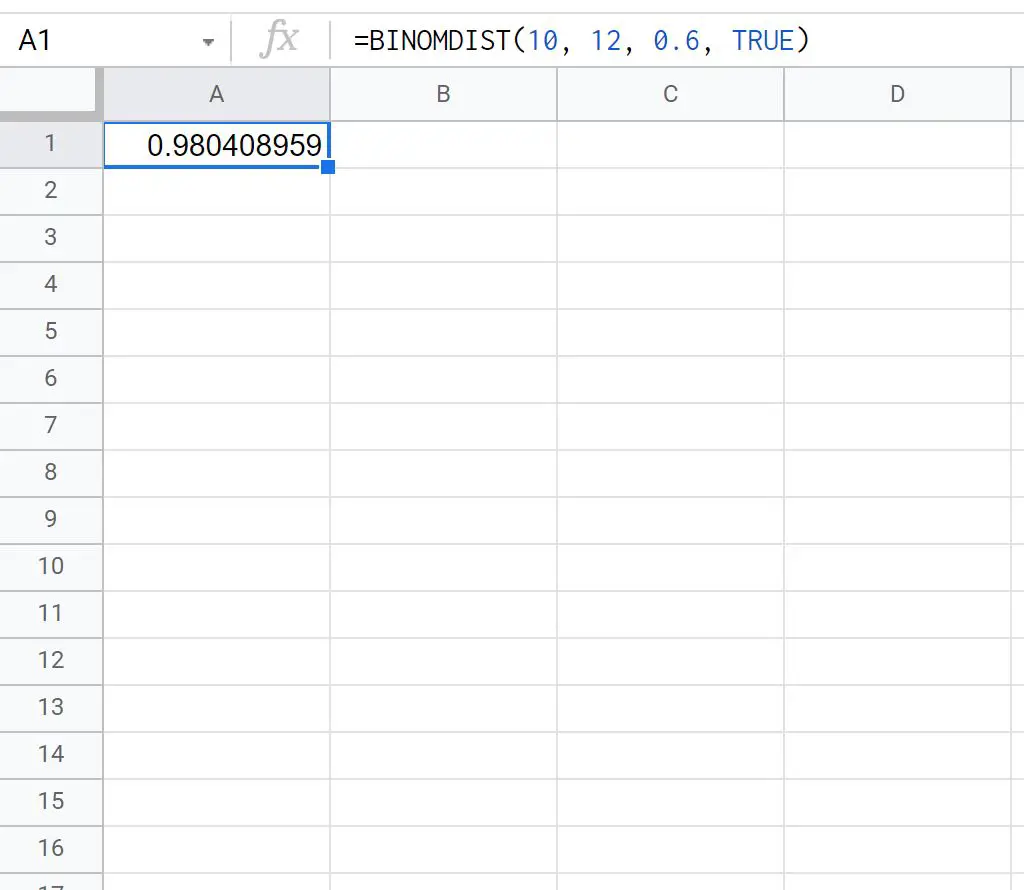
Ty 在 12 次罚球中罚中少于或等于 10 次的概率为0.9166 。
示例 4:取得更大成功的概率
Ty 的罚球命中率为 60%。如果他罚球 12 次,那么他罚球超过 10 次的概率是多少?
为了回答这个问题,我们可以在Google表格中使用以下公式:
=1- BINOMDIST ( 10 , 12 , 0.6 , TRUE )
以下屏幕截图显示了如何在实践中使用该公式:
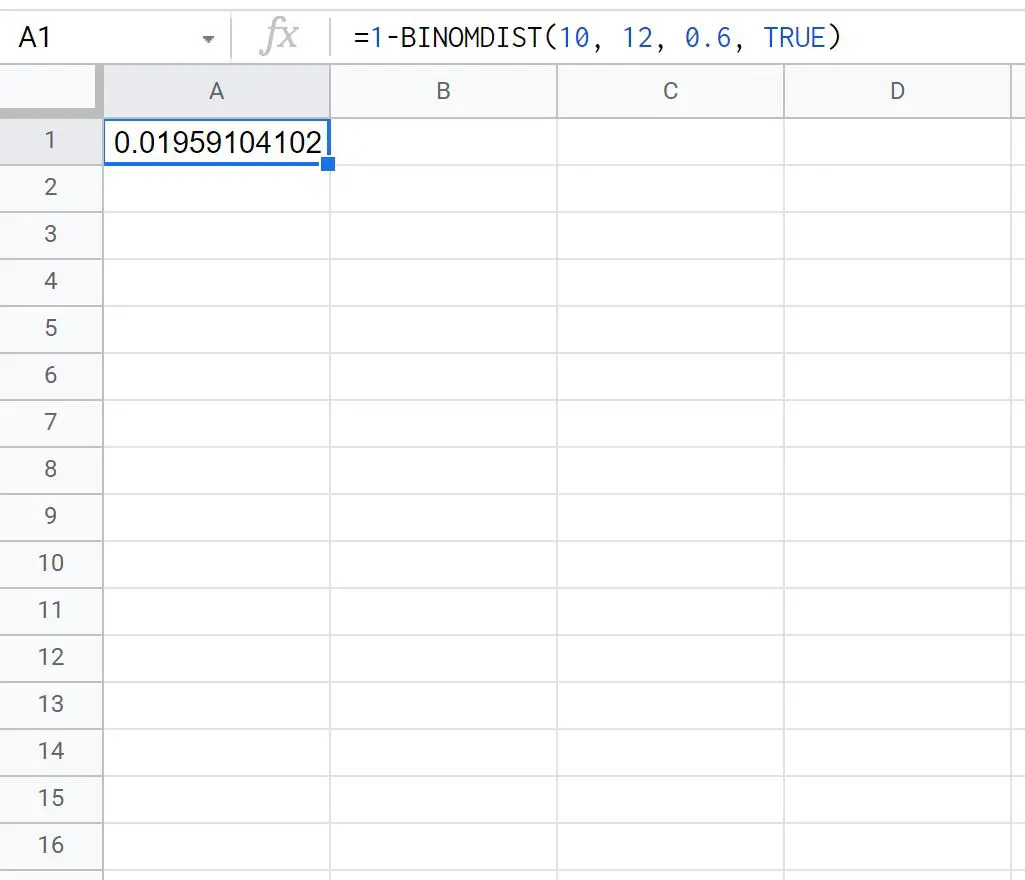
Ty 12 次罚球中超过 10 次的概率是0.0196 。
示例 5:成功概率大于或等于 k
Ty 的罚球命中率为 60%。如果他罚球 12 次,那么他总共罚中 10 次或更多的概率是多少?
为了回答这个问题,我们可以在Google表格中使用以下公式:
=1- BINOMDIST ( 9 , 12 , 0.6 , TRUE )
以下屏幕截图显示了如何在实践中使用该公式:
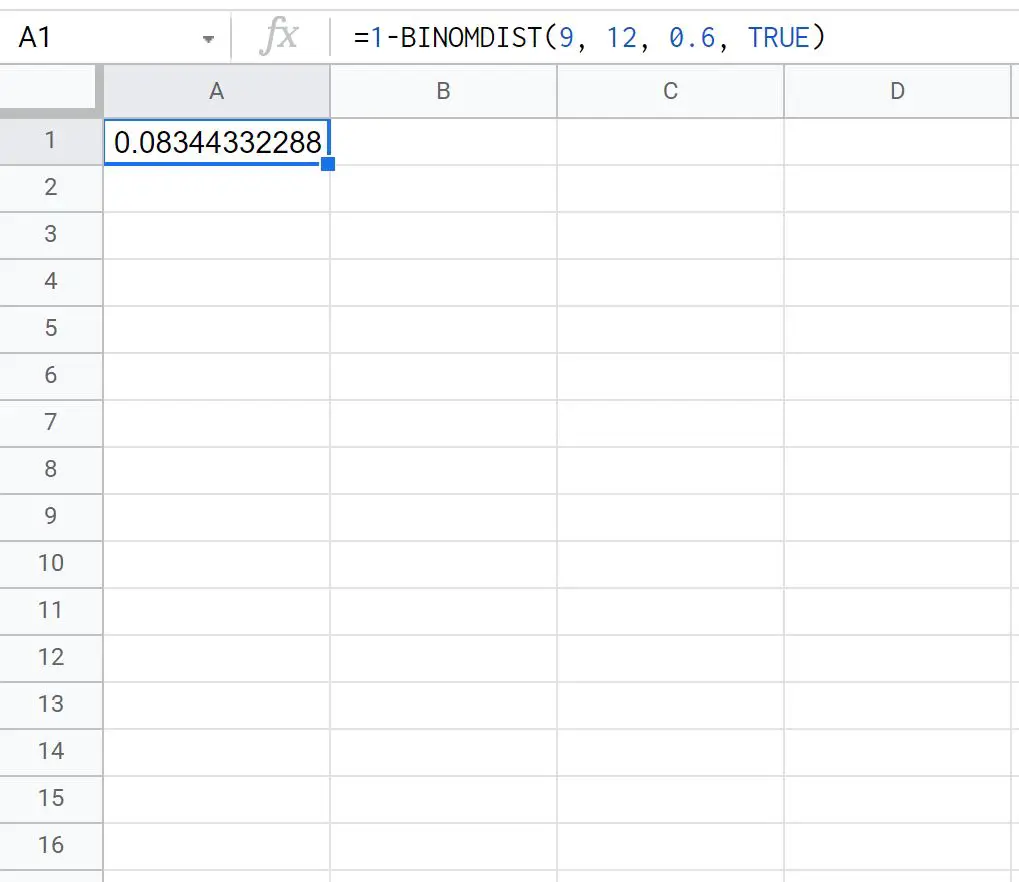
Ty 在 12 次罚球中罚球次数大于或等于 10 次的概率为0.0834 。
额外奖励:您可以使用二项式分布计算器自动计算n 、 k和p的所有值的二项式概率。
其他资源
以下教程提供有关二项式分布的更多信息: