人口均值

经过本杰明·安德森博 8月 3, 2023 统计数据 0 条评论

本文解释了人口在统计学中的含义。同样，您将了解总体平均值的公式是什么，总体平均值的置信区间是如何计算的，此外，总体平均值与“样本平均值”之间的差异是什么。

人口平均数是多少？

总体平均值是统计总体中所有元素的算术平均值。因此，要计算总体平均值，必须将所有总体值相加，然后除以总体中的元素总数。

总体平均值的符号是希腊字母μ。

类似地，总体平均值也可以定义为代表总体的变量的期望值。

了解总体平均值的定义后，让我们看看如何计算总体平均值，以更好地理解其含义。

如果统计总体中的所有值已知，则只需应用算术平均公式即可计算总体平均值。所以在这种情况下，要计算总体平均值，我们需要将所有总体值相加，然后除以数据总数。

因此，如果我们知道总体中所有元素的值，则计算总体均值的公式如下：

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

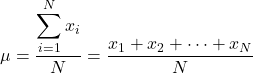
然而，一般来说，并不是所有的总体值都是已知的，因此总体平均值的值通常是通过区间来估计的。

在实践中，不可能研究总体中的所有个体，因此通常会选择总体的随机样本，并根据其值得出总体平均值的近似值。更准确地说，我们计算整个总体的均值很可能位于其中的区间；该区间称为总体平均值的置信区间。

总体平均值的置信区间是通过在样本平均值中加上和减去 Z _α/2的值乘以标准差 (σ) 再除以样本高度 (n) 的平方根来计算的。因此，总体平均值置信区间的计算公式为：

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

当总体方差已知时，使用上述公式。但是，如果总体方差未知（这是最常见的情况），则使用以下公式计算平均值的置信区间：

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

金子：

$\overline{x}$

是样本均值。
$t_{\alpha/2}$

是 n-1 个自由度的 Student t 分布的值，概率为 α/2。对于大样本量和 95% 置信水平，它通常接近 1.96；对于 99% 置信水平，它通常接近 2.576。
$s$

是样本标准差。
$n$

是样本大小。

最后，综上，我们回顾一下总体均值和样本均值之间的差异，以便明确这两个统计概念。

总体平均值和样本平均值之间的差异是计算平均值的值的范围。总体均值是整个统计总体的平均值，而样本均值是总体样本的平均值。

此外，为了区分总体平均值和样本平均值，它们由不同的符号表示。人口均值的符号是

$\mu$

，另一方面，样本均值的符号是

$\overline{x}$

。

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

如果您对这两种平均值之间的差异仍然存在疑问，或者想了解更多关于计算样本平均值的信息，您可以参考以下文章：

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多