通过原点回归：定义和示例

简单线性回归是一种可用于量化一个或多个预测变量与响应变量之间关系的方法。

简单的线性回归模型采用以下形式：

y = β ₀ + β ₁ x

金子：

• y ：响应变量的值
• β ₀ ：x = 0 时响应变量的值（称为“截距”项）
• β ₁ ：与 x 增加 1 个单位相关的响应变量的平均增加
• x ：预测变量的值

该模型的修改版本称为原点回归，当 x 等于 0 时，它强制 y 等于 0。

这种类型的模型采用以下形式：

y = _β1x

请注意，截距项已从模型中完全删除。

当研究人员知道当预测变量为零时响应变量必须为零时，有时会使用此模型。

在现实世界中，此类模型最常用于林业或生态研究。

例如，研究人员可以使用树周长来预测树高。如果给定的树的周长为零，则它的高度也必定为零。

因此，当对这些数据拟合回归模型时，原始项非零是没有意义的。

以下示例显示了拟合普通简单线性回归模型和通过原点实现回归的模型之间的差异。

示例：通过原点回归

假设生物学家想要使用树周长来拟合回归模型来预测树高。她出去收集了 15 棵树样本的以下测量值：

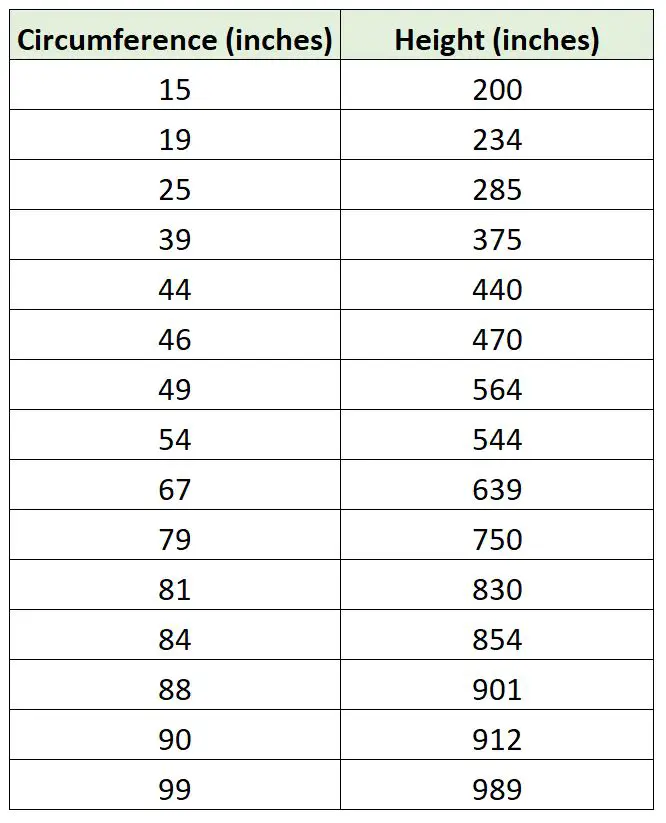
我们可以在 R 中使用以下代码来拟合一个简单的线性回归模型和一个不使用截距的回归模型，并绘制两条回归线：

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

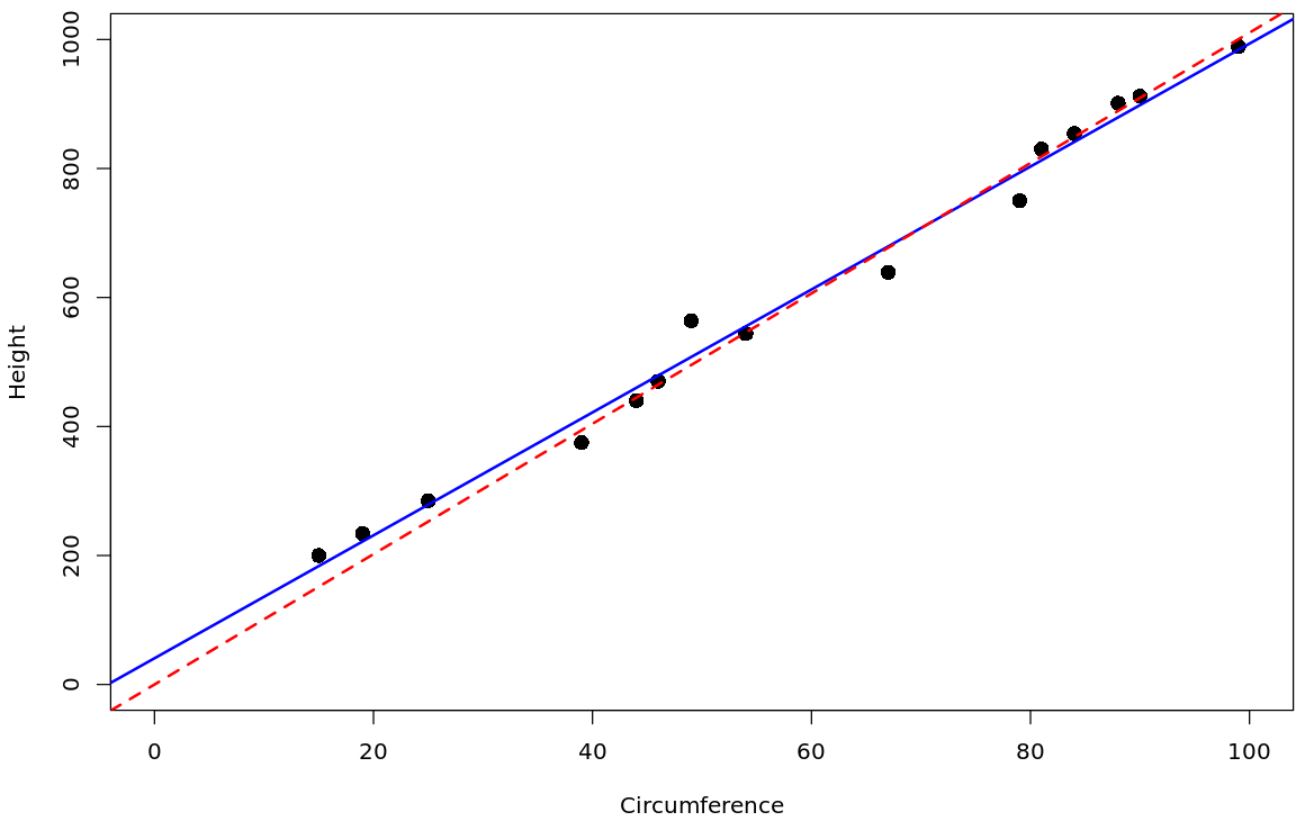
红色虚线代表经过原点的回归模型，蓝色实线代表普通的简单线性回归模型。

我们可以在 R 中使用以下代码来获取每个模型的系数估计：

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

简单线性回归模型的拟合方程为：

高度 = 40.6969 + 9.5296（周长）

回归模型通过原点的拟合方程为：

高度 = 10.1057（周长）

请注意，周长变量的系数估计值略有不同。

通过原点使用回归的注意事项

在使用截距回归之前，您必须绝对确定预测变量的值为 0 意味着响应变量的值为 0。在许多情况下，几乎不可能确定。

如果您通过原点使用回归来节省估计原点的自由度，那么如果您的样本量足够大，则很少会产生实质性差异。

如果您选择通过原点使用回归，请务必在最终分析或报告中概述您的推理。

其他资源

以下教程提供有关线性回归的其他信息：

简单线性回归简介
多元线性回归简介
如何阅读和解释回归表