伯努利分布和二项分布:有什么区别?
如果随机变量只有两种可能的结果:0 或 1,则它遵循伯努利分布。
例如,假设我们扔了一次硬币。让p 。这意味着它落地的概率是 1- p 。
所以,我们可以写:
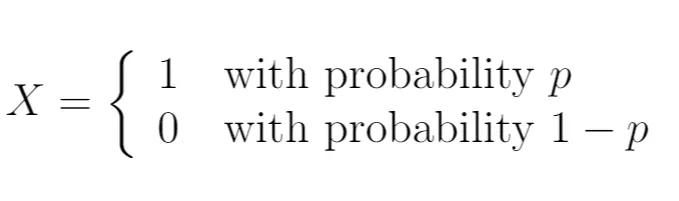
在这种情况下,随机变量X服从伯努利分布。它只能采用两个可能的值。
现在,如果我们多次抛硬币,伯努利随机变量的总和将服从二项式分布。
例如,假设我们抛硬币 5 次,想知道k次出现正面朝上的概率。它看起来像随机变量
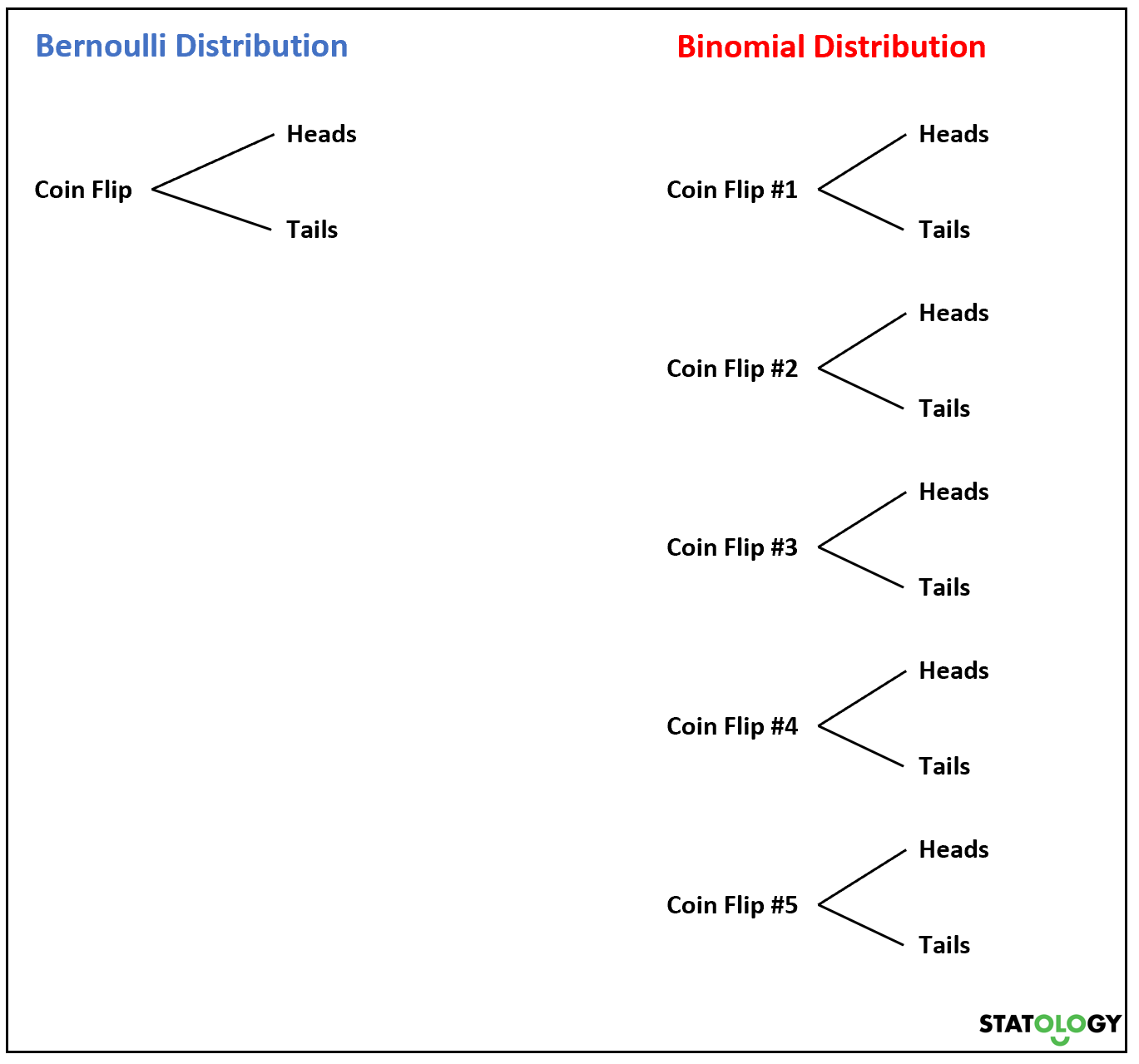
如果随机变量X服从二项式分布,则X = k成功的概率可以通过以下公式求出:
P(X=k) = n C k * p k * (1-p) nk
金子:
- n:试验次数
- k:成功次数
- p:给定试验的成功概率
- n C k :在n次试验中获得k次成功的方法数
例如,假设我们抛硬币 3 次。我们可以使用上面的公式来确定这 3 次翻转中获得 0 次正面的概率:
P(X=0) = 3 C 0 * 0.5 0 * (1-0.5) 3-0 = 1 * 1 * (0.5) 3 = 0.125
当n = 1 次试验时,二项式分布等效于伯努利分布。
重要笔记
以下是有关伯努利分布和二项式分布的一些重要说明:
1. 服从伯努利分布的随机变量只能取两个可能的值,但服从二项式分布的随机变量可以取多个值。
例如,在一次抛硬币中,我们要么得到 0 个正面,要么得到 1 个正面。然而,在一系列 5 次抽奖中,我们可能会出现 0、1、2、3、4 或 5 个正面。
2. 对于服从二项式分布的随机变量,每次伯努利试验“成功”的概率必须相等且独立。
例如,如果我们将“成功”定义为正面落地,那么每次抛掷成功的概率为0.5,并且每次抛掷都是独立的——一次抛掷的结果不会影响另一次抛掷的结果。