估计的标准误差是多少？ （定义&；示例）
估计的标准误差是衡量回归模型预测准确性的一种方法。
通常称为 σ est ，其计算公式如下：
σ = √ Σ(y – ŷ) 2 /n
金子：
- y：观测值
- ŷ：预测值
- n：观察总数
估计的标准误差让我们了解回归模型对数据集的拟合程度。尤其：
- 值越小，拟合越好。
- 值越大，拟合度越差。
对于估计标准误差较小的回归模型，数据点将紧密聚集在估计回归线周围：
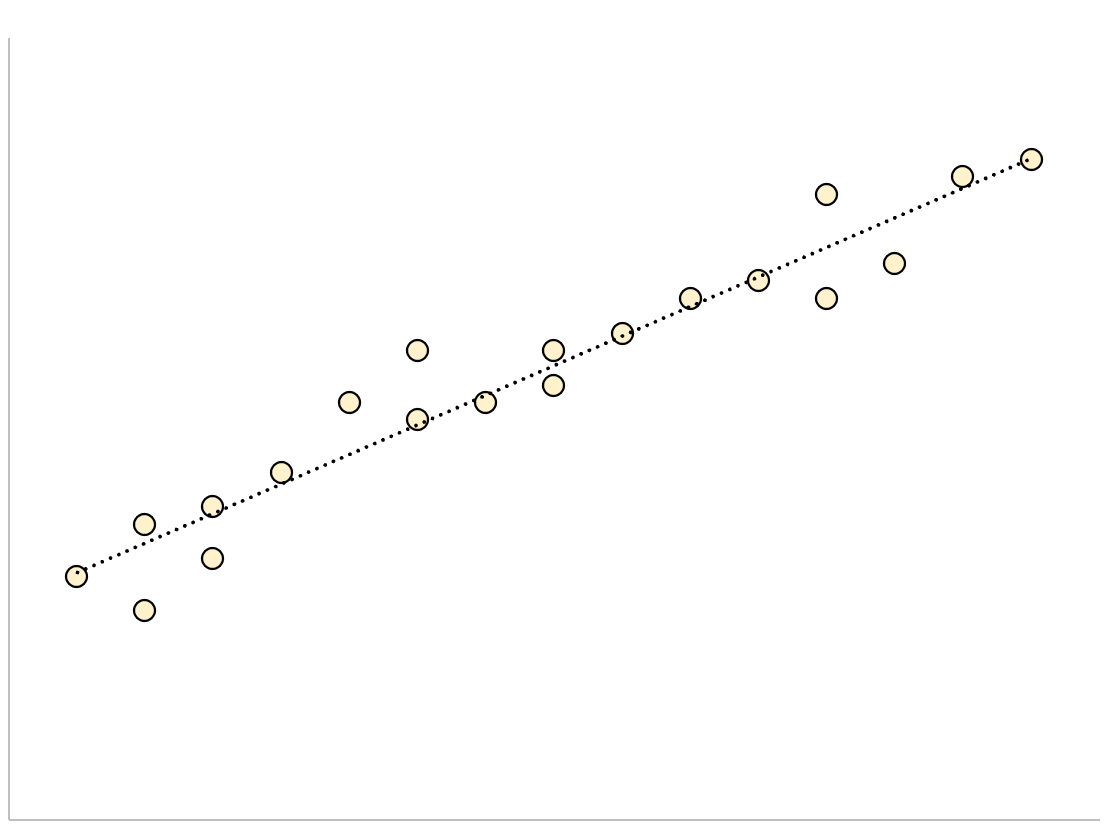
相反，对于估计标准误差较大的回归模型，数据点将更加松散地分散在回归线周围：
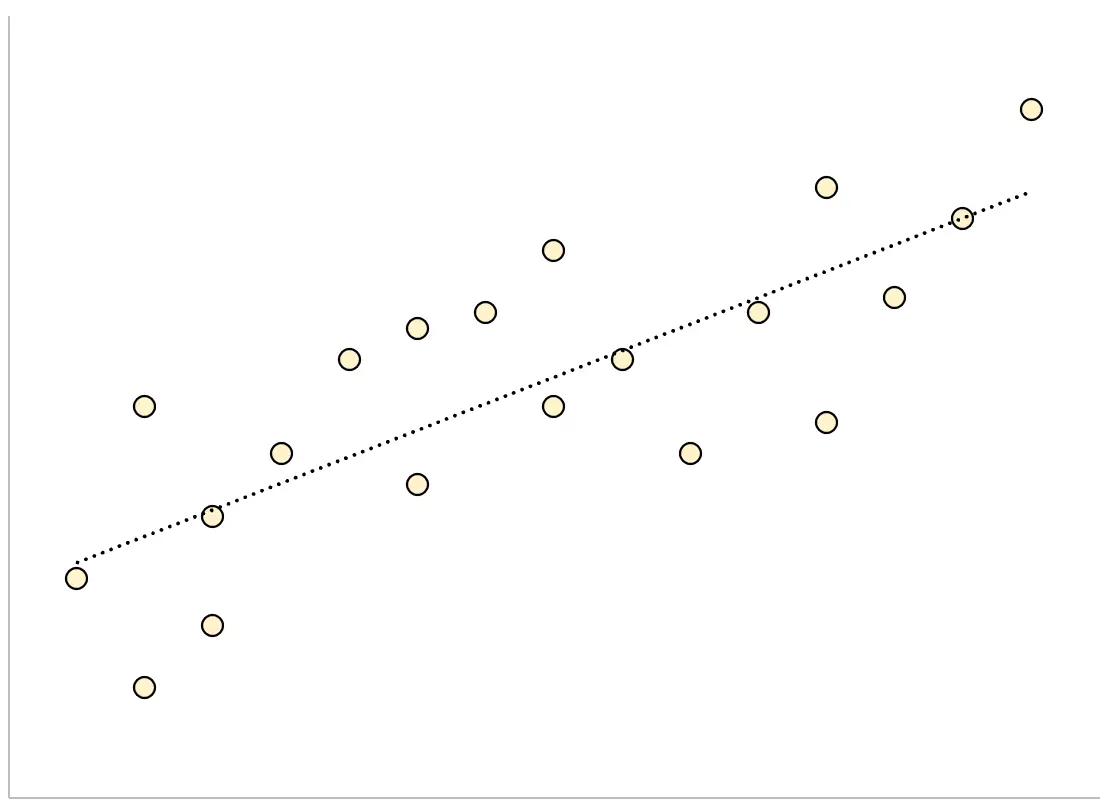
以下示例演示如何在 Excel 中计算和解释回归模型估计值的标准误差。
示例：Excel 中估计的标准误差
使用以下步骤计算 Excel 中回归模型的估计值的标准误差。
第 1 步：输入数据
首先，输入数据集值：
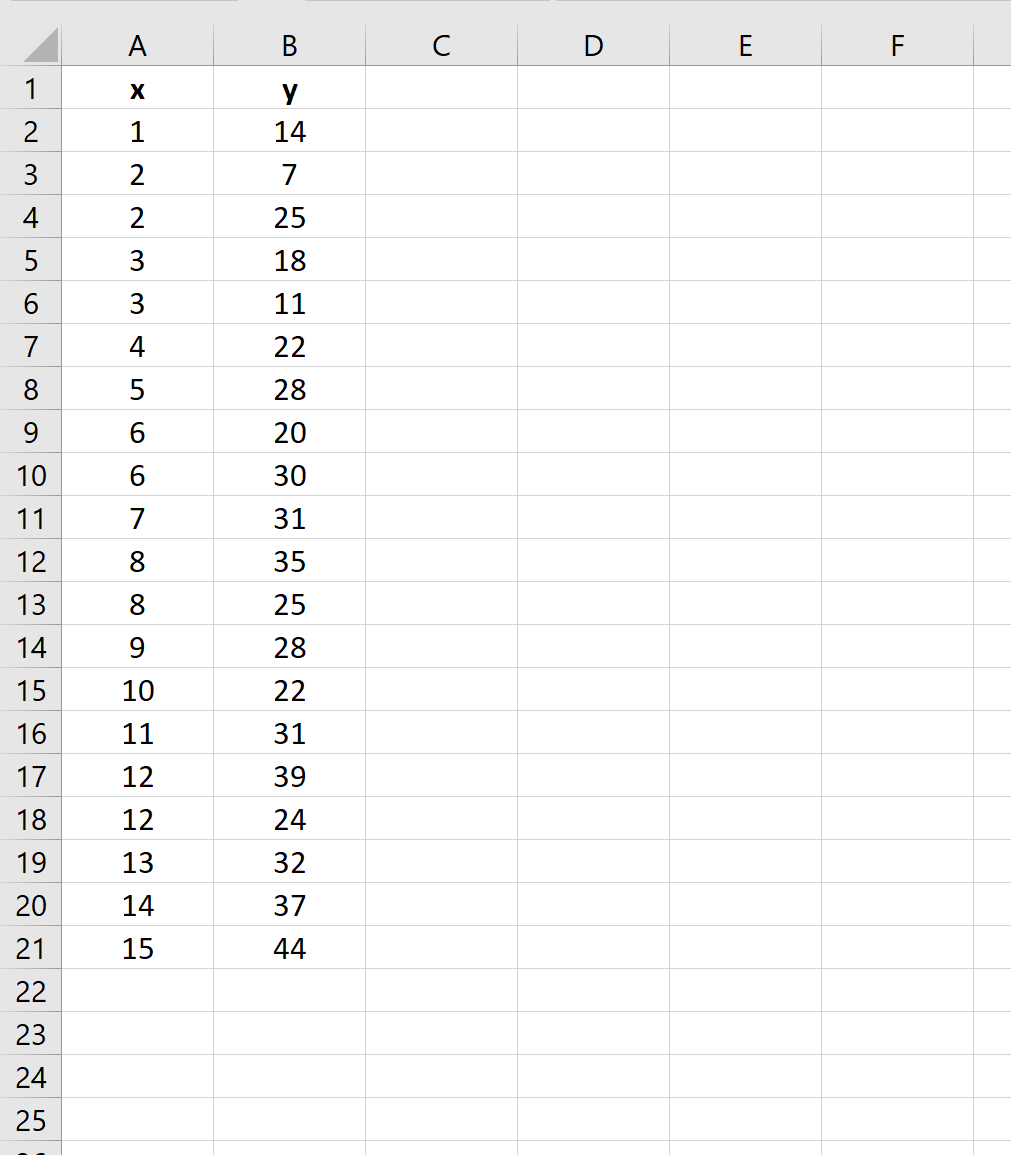
第 2 步：执行线性回归
接下来，单击顶部功能区的“数据”选项卡。然后单击“分析”组中的“数据分析”选项。
如果您没有看到此选项，则必须首先加载分析工具库。
在出现的新窗口中，单击回归，然后单击确定。
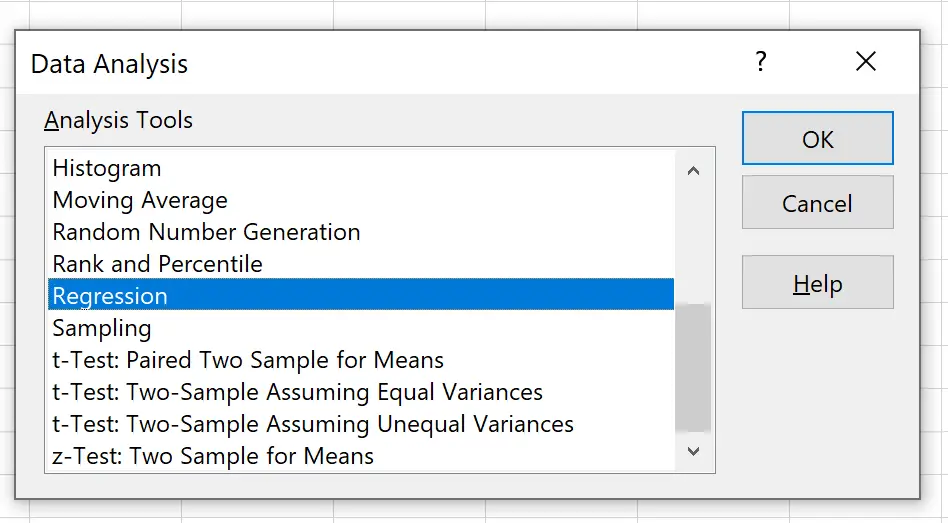
在出现的新窗口中，提供以下信息：
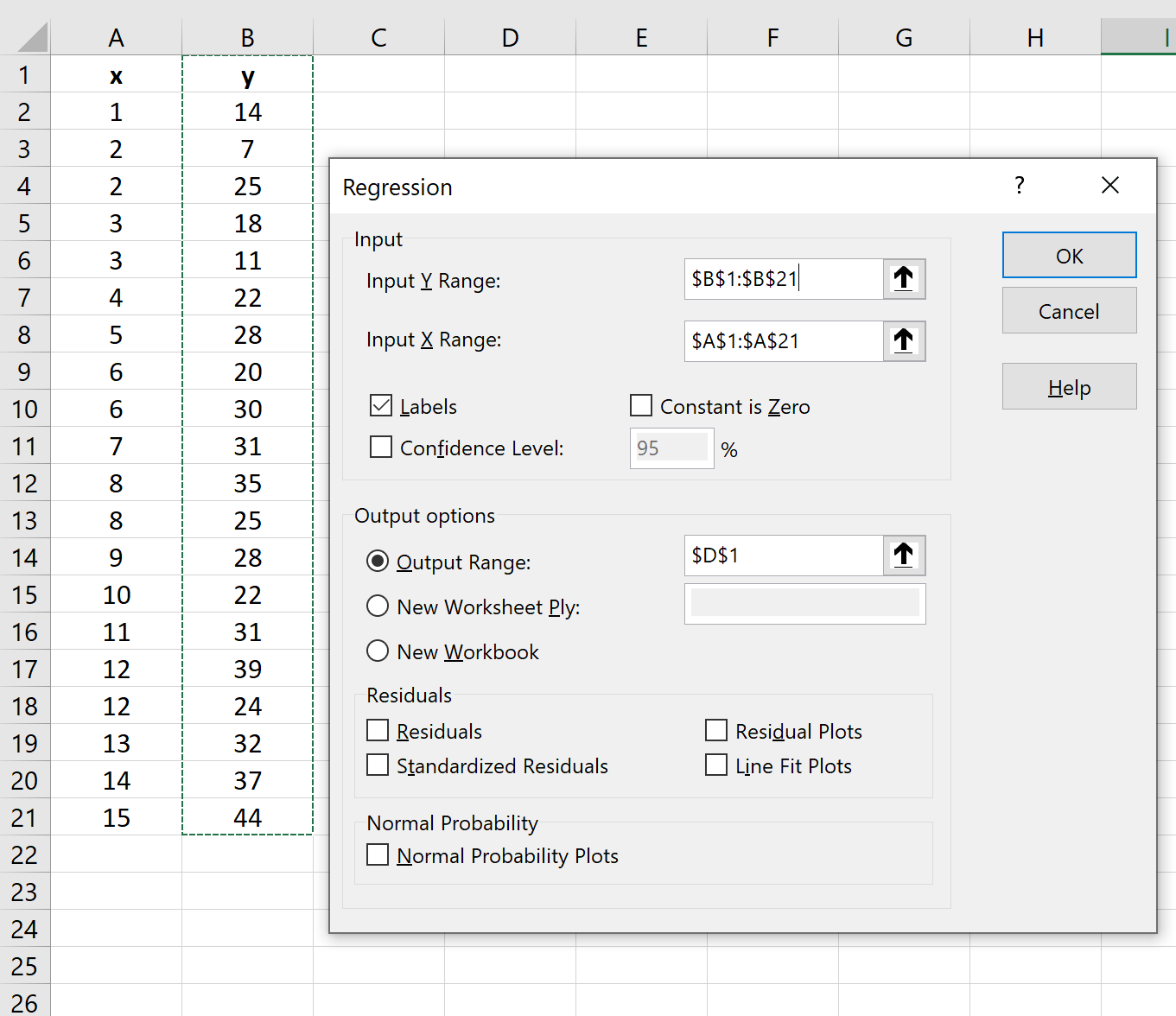
单击“确定”后，将出现回归结果：
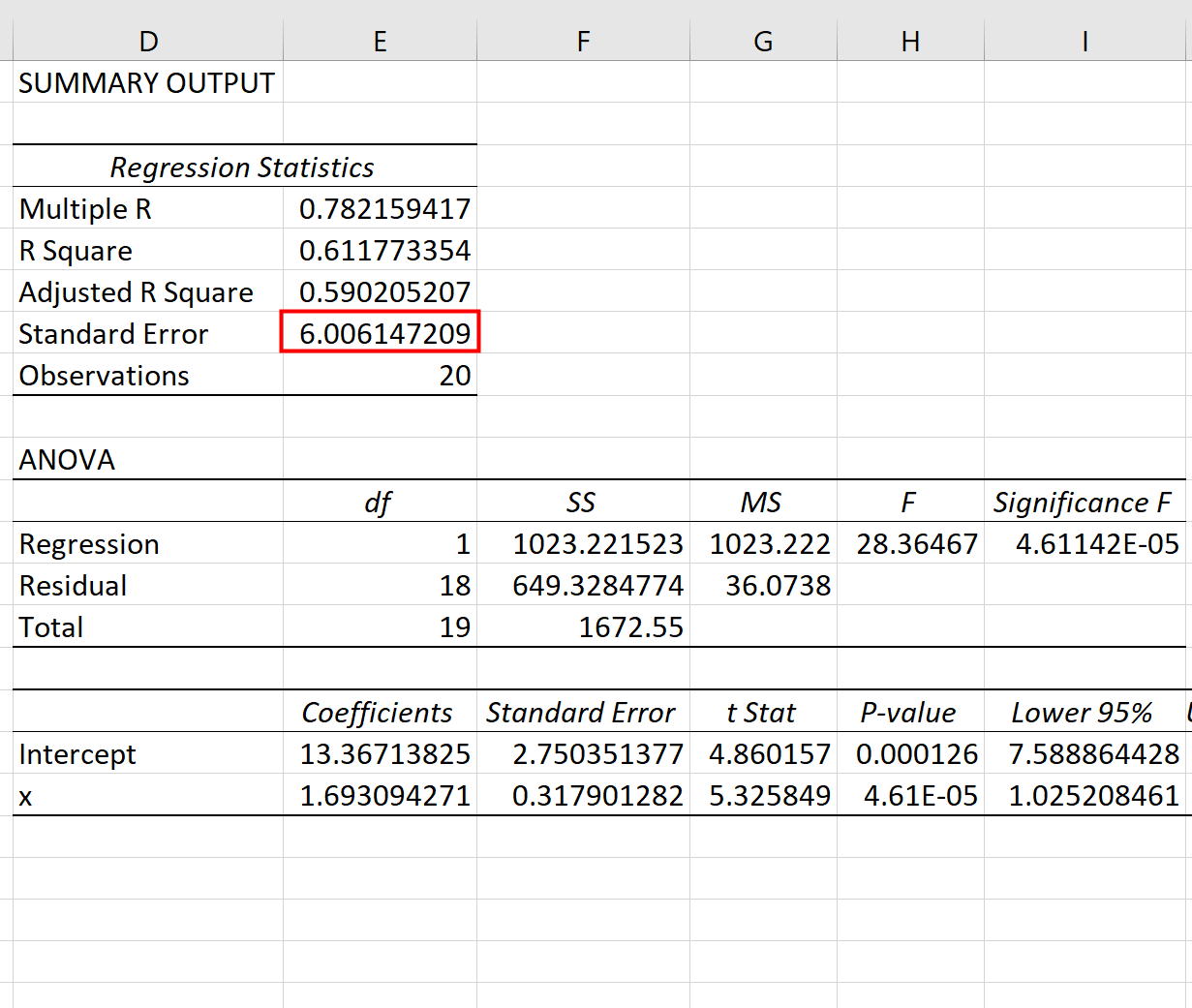
我们可以使用回归表中的系数来构建估计的回归方程：
ŷ = 13.367 + 1.693(x)
我们可以看到该回归模型估计的标准误差为6.006 。简单来说，这告诉我们平均数据点距回归线6.006 个单位。
我们可以使用估计的回归方程和估计的标准误差来构建某个数据点的预测值的 95% 置信区间。
例如，假设 x 等于 10。使用估计的回归方程，我们可以预测 y 等于：
ŷ = 13.367 + 1.693*(10) = 30.297
我们可以使用以下公式获得该估计的 95% 置信区间：
- 95% CI = [ŷ – 1.96*σ为, ŷ + 1.96*σ为]
对于我们的示例，95% 置信区间的计算方式如下：
- 95% CI = [ŷ – 1.96*σ为, ŷ + 1.96*σ为]
- 95% CI = [30.297 – 1.96*6.006, 30.297 + 1.96*6.006]
- 95% CI = [18,525, 42,069]
其他资源
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多