如何解释比例和位置图：举例

缩放位置图是一种图表，它沿 x 轴显示回归模型的拟合值，沿 y 轴显示标准化残差的平方根。

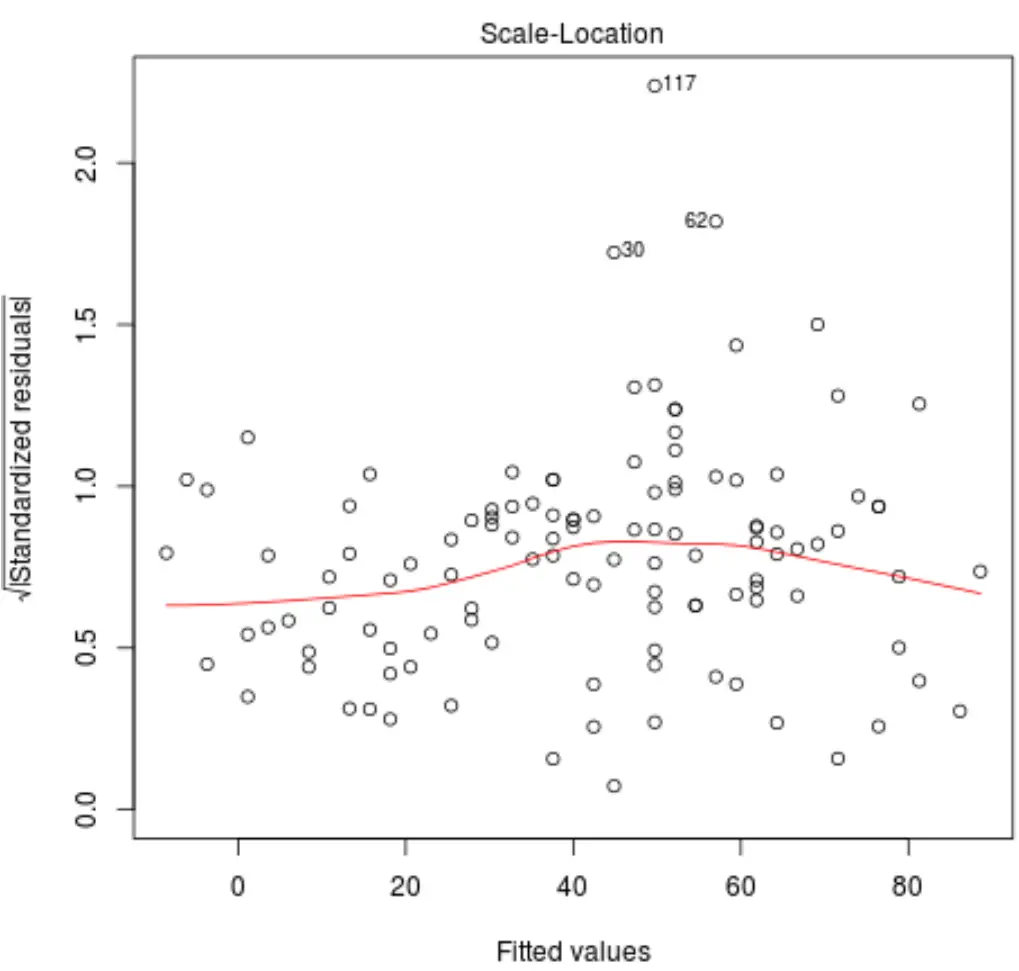
看看这个图，我们检查两件事：

1.验证绘图上的红线是否大致水平。如果是这种情况，则对于给定的回归模型可能满足同方差性假设。也就是说，所有拟合值的残差分布近似相等。

2.检查残差之间是否没有明显的趋势。换句话说，残差应随机分散在红线周围，所有拟合值的变异性大致相等。

R 中的比例和位置绘图

我们可以使用以下代码在 R 中拟合一个简单的线性回归模型，并为结果模型生成比例和位置图：

 #fit simple linear regression model
model <- lm(Ozone ~ Temp, data = airquality)

#produce scale-location plot
plot(model)

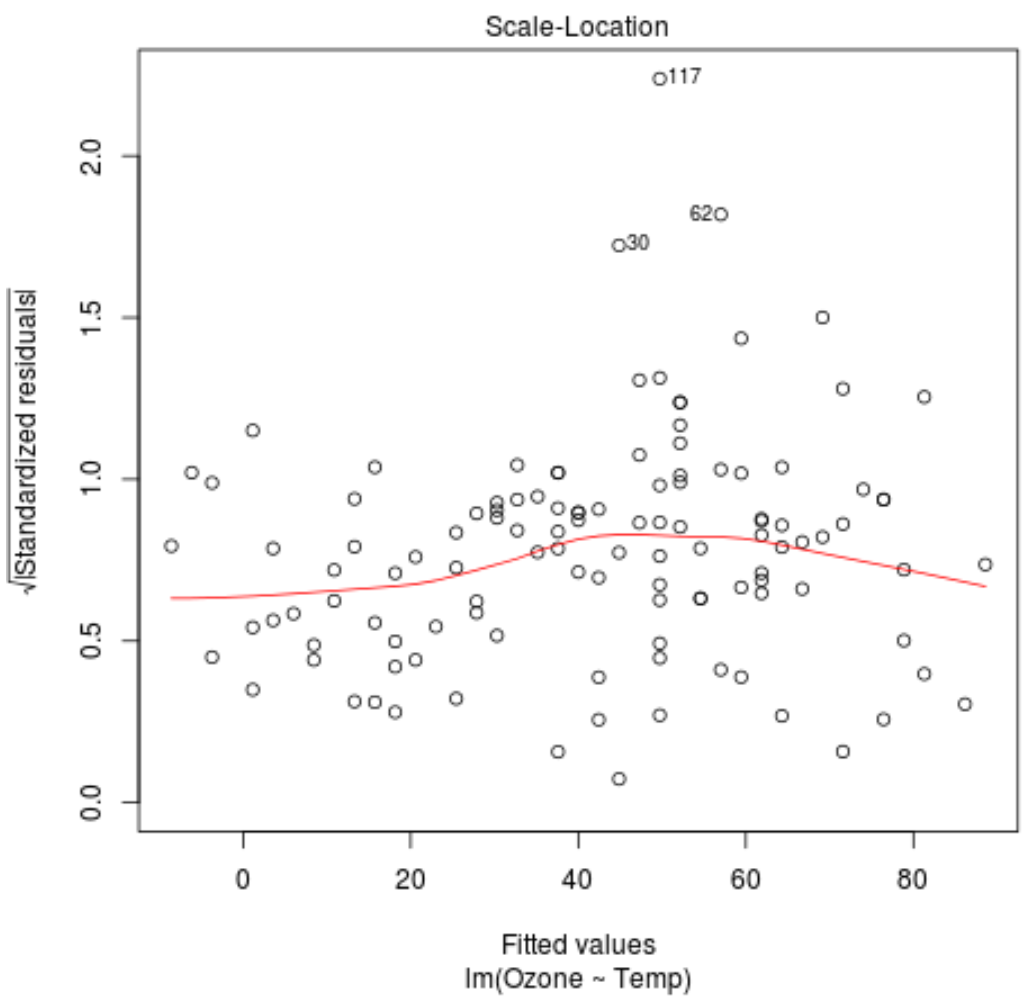
我们可以从该回归模型的尺度位置图中观察到以下两件事。

1.红线在图上大致水平。如果是这种情况，则对于给定的回归模型，满足同方差性假设。也就是说，所有拟合值的残差分布近似相等。

2.检查残差之间是否没有明显的趋势。换句话说，残差应随机分散在红线周围，所有拟合值的变异性大致相等。

技术说明

数据集中具有最高标准化残差的三个观测值在图中进行了标记。

我们可以看到第 30、62 和 117 行中的观测值具有最高的标准化残差。

这并不一定意味着这些观察结果是异常值，但您可能需要查看原始数据以更仔细地检查这些观察结果。

尽管我们可以看到红线在尺度位置图上大致水平，但这仅作为视觉方式来查看是否满足同方差性假设。

我们可以用来查看是否满足同方差性假设的正式统计检验是Breusch-Pagan 检验。

R 中的 Breusch-Pagan 测试

以下代码展示了如何使用lmtest包的bptest()函数在 R 中执行 Breusch-Pagan 测试：

 #load lmtest package
library(lmtest)

#perform Breusch-Pagan Test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 1.4798, df = 1, p-value = 0.2238

Breusch-Pagan 检验使用以下原假设和备择假设：

• 零假设 (H ₀ )：残差是同方差的（即均匀分布）
• 备择假设 ( _HA )：残差是异方差的（即不均匀分布）

从结果中，我们可以看到检验的 p 值为0.2238 。由于该 p 值不小于 0.05，因此我们无法拒绝原假设。我们没有足够的证据表明回归模型中存在异方差。

该结果与我们对比例位置图中红线的目视检查相符。

其他资源

了解回归分析中的异方差性
如何在 R 中创建残差图
如何在 R 中执行 Breusch-Pagan 测试