何时使用岭和套索回归

在普通的多元线性回归中，我们使用一组p 个预测变量和一个响应变量来拟合以下形式的模型：

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

β ₀ 、β ₁ 、B ₂ 、…、β _p的值使用最小二乘法选择，该方法最小化残差平方和 (RSS)：

RSS = Σ(y _i – ŷ _i ) ²

金子：

• Σ ：表示“和”的符号
• y _i ：^{第 i 个}观测值的实际响应值
• ŷ _i ：第 i^个观测值的预测响应值

回归中的多重共线性问题

多元线性回归实践中经常出现的一个问题是多重共线性——当两个或多个预测变量彼此高度相关时，它们不会在回归模型中提供唯一或独立的信息。

这可能会使模型系数估计不可靠并表现出较高的方差。也就是说，当模型应用于以前从未见过的新数据集时，它很可能表现不佳。

避免多重共线性：Ridge & Lasso 回归

我们可以用来解决这个多重共线性问题的两种方法是岭回归和套索回归。

岭回归旨在最小化以下因素：

• RSS + λΣβ _j ²

Lasso 回归旨在最小化以下因素：

• RSS + λΣ|β _j |

在这两个方程中，第二项称为退出惩罚。

当 λ = 0 时，该惩罚项不起作用，岭回归和套索回归产生与最小二乘相同的系数估计。

然而，当 λ 接近无穷大时，收缩惩罚变得更具影响力，并且模型中不可导入的预测变量会减少到零。

使用 Lasso 回归，当 λ 变得足够大时，某些系数可能完全为零。

Ridge & Lasso 回归的优点和缺点

Ridge 和 Lasso 回归相对于最小二乘回归的优势在于 偏差-方差权衡。

回想一下，均方误差 (MSE) 是我们可以用来衡量给定模型准确性的指标，其计算公式如下：

MSE = Var( f̂( x ₀ )) + [偏差( f̂( x ₀ ))] ² + Var(ε)

MSE = 方差 + 偏差² + 不可约误差

Ridge Regression和Lasso Regression的基本思想是引入一个小的偏差，使得方差可以显着减小，从而导致整体MSE较低。

为了说明这一点，请考虑下图：

请注意，随着 λ 的增加，方差显着减小，而偏差的增加非常小。然而，超过某一点后，方差下降的速度会减慢，系数的下降会导致系数的显着低估，从而导致偏差急剧增加。

从图中我们可以看出，当我们选择在偏差和方差之间产生最佳权衡的 λ 值时，检验的 MSE 最低。

当 λ = 0 时，套索回归中的惩罚项不起作用，因此产生与最小二乘相同的系数估计。然而，通过将 λ 增加到某个点，我们可以降低测试的整体 MSE。

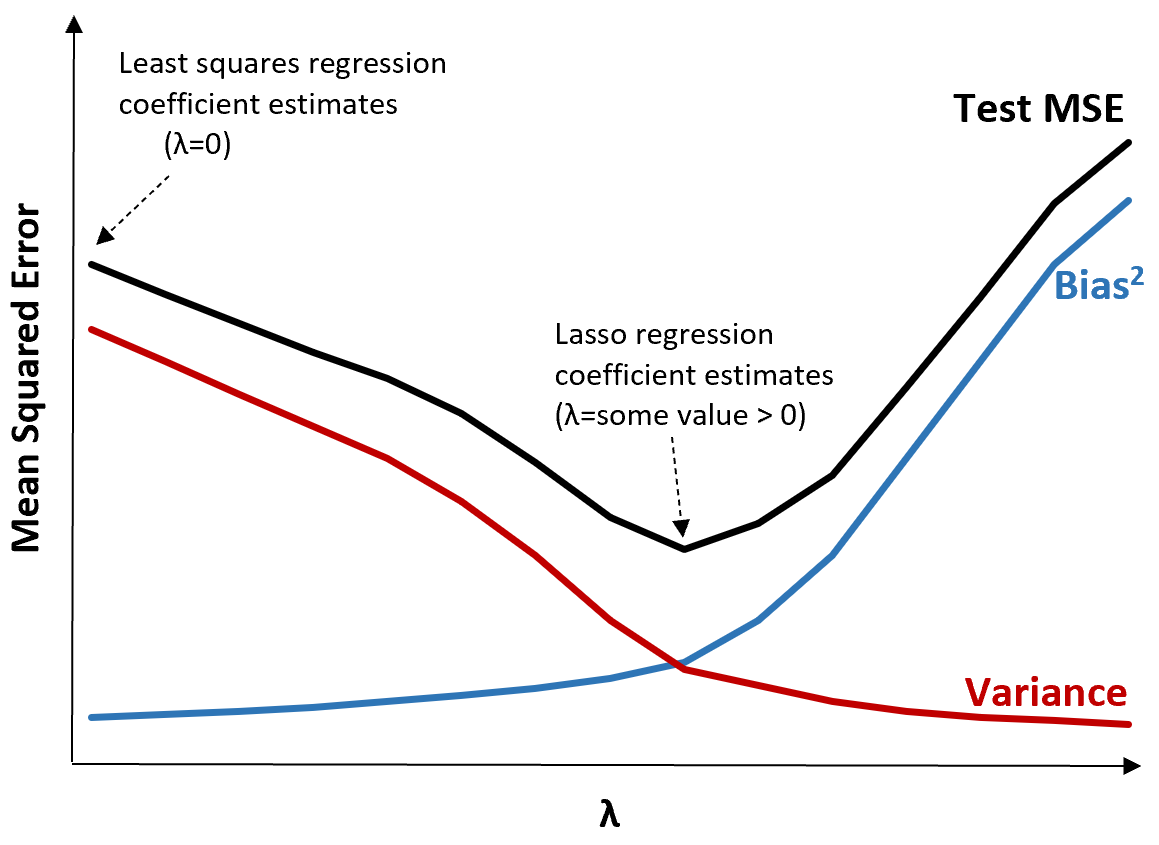
这意味着通过岭和套索回归进行的模型拟合可能比通过最小二乘回归进行的模型拟合产生更小的测试误差。

Ridge 和 Lasso 回归的缺点是，当最终模型中的系数向零收缩时，解释它们会变得困难。

因此，当您想要优化预测能力而不是推理时，应使用 Ridge 和 Lasso 回归。

里奇VS里奇套索回归：何时使用每个回归

拉索回归和岭回归被称为正则化方法，因为它们都试图最小化残差平方和（RSS）以及某个惩罚项。

换句话说，它们限制或规范了模型系数的估计。

这自然提出了一个问题：岭回归和套索回归哪个更好？

在只有少量预测变量显着的情况下，套索回归往往效果更好，因为它能够将不显着的变量完全减少到零并将其从模型中删除。

然而，当许多预测变量在模型中显着并且它们的系数近似相等时，岭回归往往效果更好，因为它将所有预测变量保留在模型中。

为了确定哪个模型最适合进行预测，我们通常执行k 倍交叉验证并选择产生最低测试均方根误差的模型。

其他资源

以下教程介绍了岭回归和套索回归：

• 岭回归简介
• 套索回归简介

以下教程解释了如何在 R 和 Python 中执行两种类型的回归：

• R 中的岭回归
• Python 中的岭回归
• R 中的套索回归
• Python 中的套索回归