何时使用 spearman 等级相关(2 个场景)
量化两个变量之间线性关联的最常见方法是使用Pearson 相关系数,该系数始终取 -1 到 1 之间的值,其中:
- -1表示完全负线性相关
- 0 表示没有线性相关
- 1 表示完全正线性相关
然而,当两个变量之间真正的潜在关系是线性时,这种类型的相关系数效果最好。
还有另一种相关系数,称为斯皮尔曼等级相关,最适合在两种特定场景中使用:
场景 1 :处理机密数据时。
- 一个示例可以是包含学生数学考试成绩排名以及班级中科学考试成绩排名的数据集。
场景 2 :当存在一个或多个极端异常值时。
- 当数据集中存在极端异常值时,皮尔逊相关系数会受到很大影响。
以下示例展示了如何计算每种情况下的 Spearman 等级相关性。
场景 1:将 Spearman 排名与排名数据相关联
考虑以下显示两个变量之间关系的数据集(以及相应的散点图):

使用统计软件,我们可以计算这两个变量的以下相关系数:
- 皮尔逊相关系数: 0.79
- 斯皮尔曼等级相关性: 1
在这种情况下,如果我们只关心数据值的排名(随着 x 的排名增加,y 的排名也会增加吗?),那么 Spearman 的排名相关性会让我们更好地了解两个变量之间的相关性。 。
在这个特定的数据集中,随着 x 的排名增加,y 的排名总是增加。
Spearman 的等级相关性通过告诉我们 x 的等级和 y 的等级之间存在完美的正关系 ( ρ = 1 ),完美地捕捉了这种行为。
另一方面,皮尔逊相关性告诉我们,两个变量之间存在很强的线性关系( r = 0.79 )。
这是事实,但是如果我们只关心 x 的秩和 y 的秩之间的关系,那么它是没有用的。
场景 2:Spearman 排名与极端异常值的相关性
考虑以下显示两个变量之间关系的数据集(以及相应的散点图):
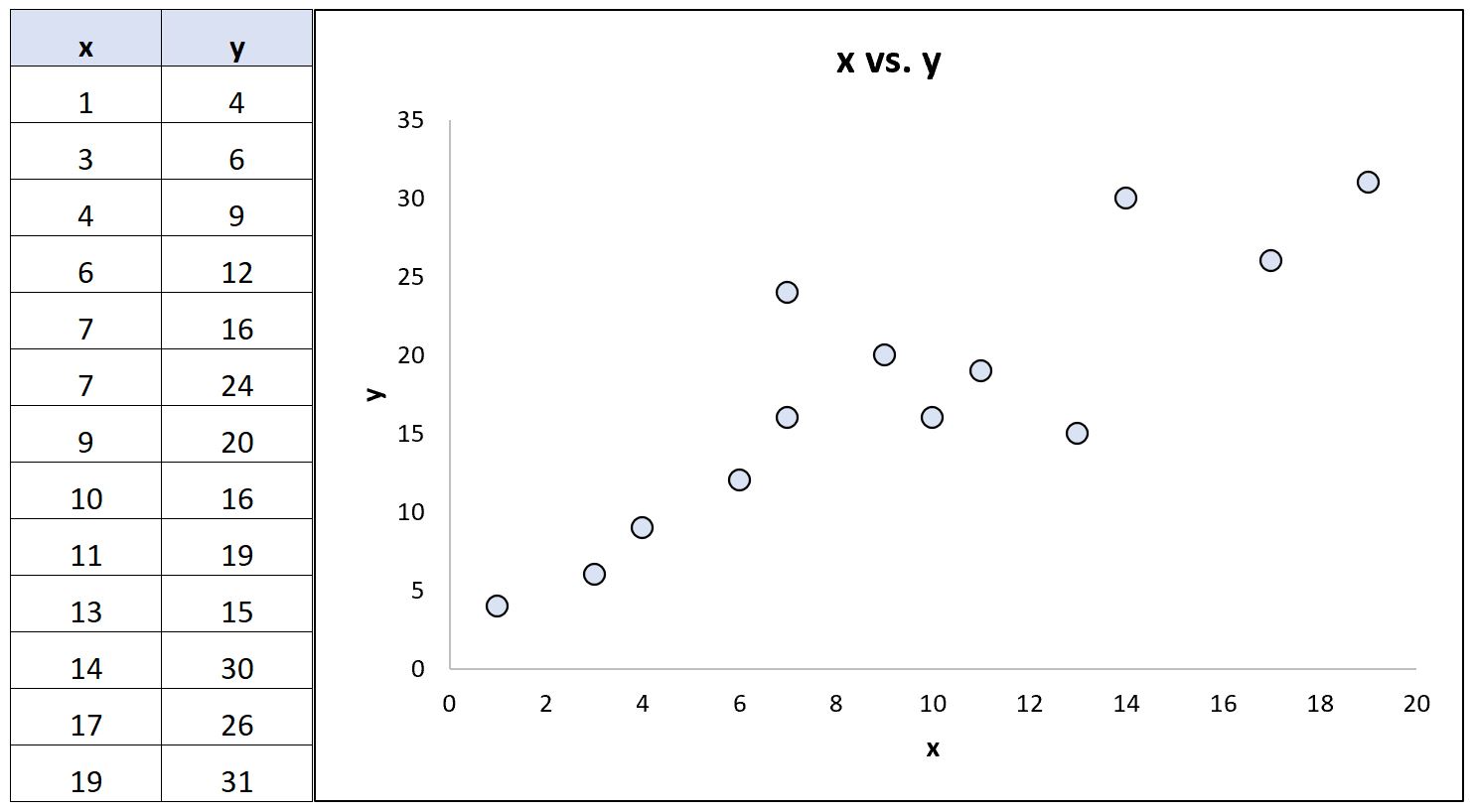
使用统计软件,我们可以计算这两个变量的以下相关系数:
- 皮尔逊相关系数: 0.86
- 斯皮尔曼等级相关性: 0.85
相关系数几乎相同,因为变量之间的基本关系近似线性并且不存在极端异常值。
现在假设我们更改数据集中的最后一个 y 值,使其成为极端异常值:
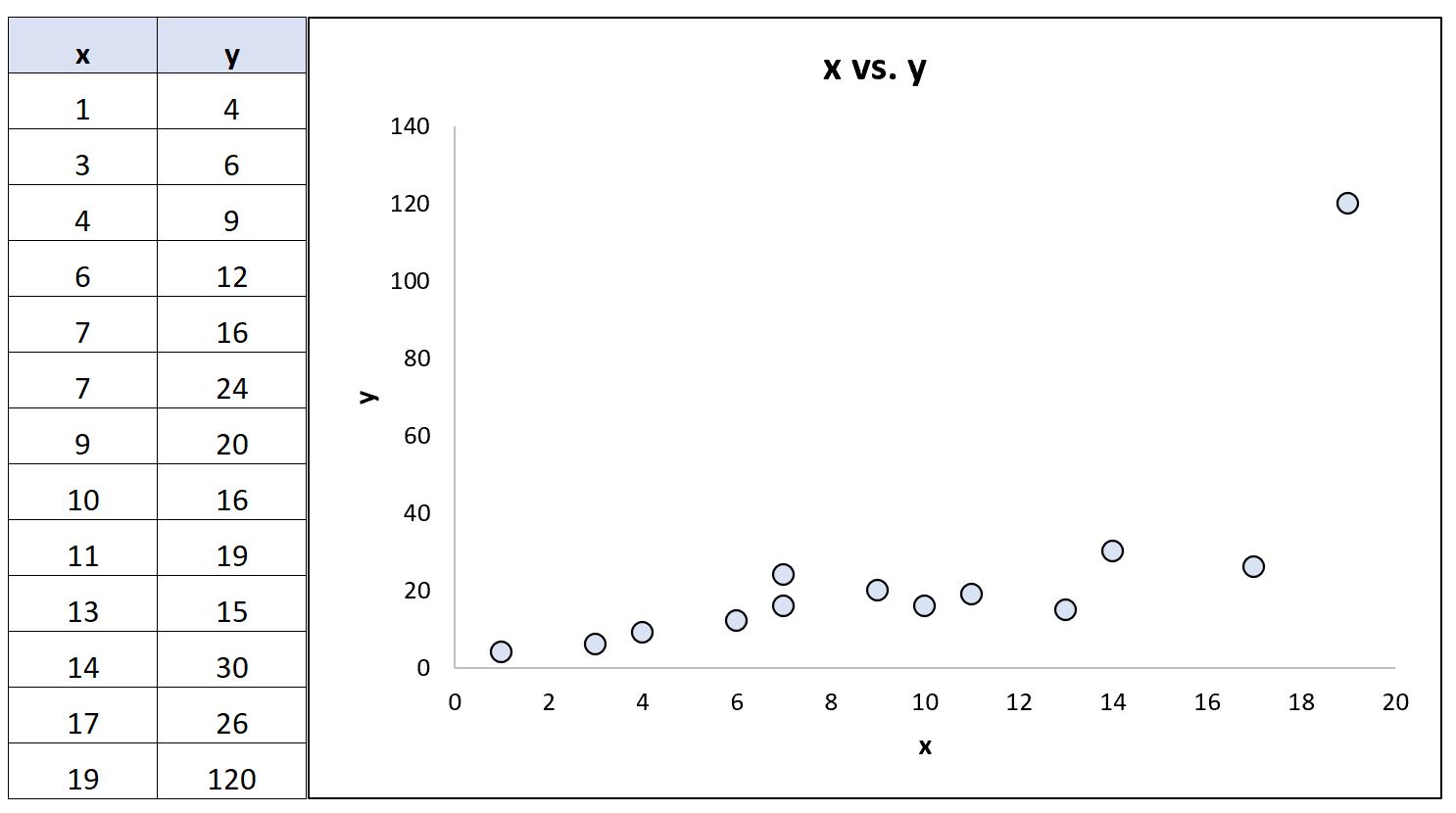
使用统计软件,我们可以重新计算相关系数:
- 皮尔逊相关系数: 0.69
- 斯皮尔曼等级相关性: 0.85
Pearson 相关系数显着变化,而 Spearman 等级相关系数保持不变。
使用统计术语,我们可以说 x 和 y 之间的关系是单调的(随着 x 的增加,y 通常会增加),但不是线性的,因为异常值对数据影响很大。
在这种情况下,斯皮尔曼的等级相关性很好地量化了这种单调关系,而皮尔逊的相关性则表现不佳,因为它试图计算两个变量之间的线性关系。
相关: 如何以 APA 格式报告 Spearman 等级相关性
其他资源
以下教程解释了如何使用不同的软件计算 Spearman 等级相关性:
如何在 Excel 中计算 Spearman 等级相关性
如何在 Google 表格中计算 Spearman 排名相关性
如何在 R 中计算 Spearman 等级相关
如何在 Python 中计算斯皮尔曼等级相关性