什么时候应该使用相关性？ （解释和示例）

相关性用于衡量两个变量之间的线性关联。

相关系数始终取 -1 和 1 之间的值，其中：

• -1 表示两个变量之间完全负线性相关
• 0 表示两个变量之间不存在线性相关
• 1 表示两个变量之间存在完全正线性相关

学生经常问的一个问题是：什么时候应该使用相关性？

简短的答案：当您想要量化两个变量之间的线性关系并且两个变量都不代表响应或“结果”变量时，请使用相关性。

以下示例说明了在实践中何时应该使用相关性，何时不应该使用相关性。

示例 1：何时使用相关性

假设一位教授想要了解他班上学生的数学考试成绩和科学考试成绩之间的线性关系。

例如，在数学考试中表现良好的学生在科学考试中也表现良好吗？或者数学得分高的学生往往在科学得分低？

在这种情况下，他可以计算数学考试成绩和科学考试成绩之间的相关性，因为他只是想了解两个变量之间的线性关系，并且两个变量都不能被视为响应变量。

假设他计算Pearson 相关系数，发现 r = 0.78。这是一种很强的正相关性，这意味着在数学方面表现良好的学生也往往在科学方面表现良好。

示例 2：何时不使用相关性

假设一家公司的营销部门想要量化广告支出对总收入的影响。

例如，每多花一美元在广告上，公司预计可以获得多少额外收入？

在这种情况下，该部门必须使用线性回归模型来量化广告支出与总收入之间的关系，因为“收入”变量是响应变量。

假设该部门应用简单的线性回归模型，发现以下方程最能描述广告支出与总收入之间的关系：

总收入 = 145.4 + 0.34*（广告费用）

我们将此解释为，广告上每增加 1 美元，总收入就会平均增加 0.34 美元。

使用相关性的注意事项

需要注意的是，相关性只能用于量化两个变量之间的线性关系。

然而，在某些情况下，相关系数将无法有效地捕捉共享非线性关系的两个变量之间的关系。

例如，假设我们创建以下散点图来可视化两个变量之间的关系：

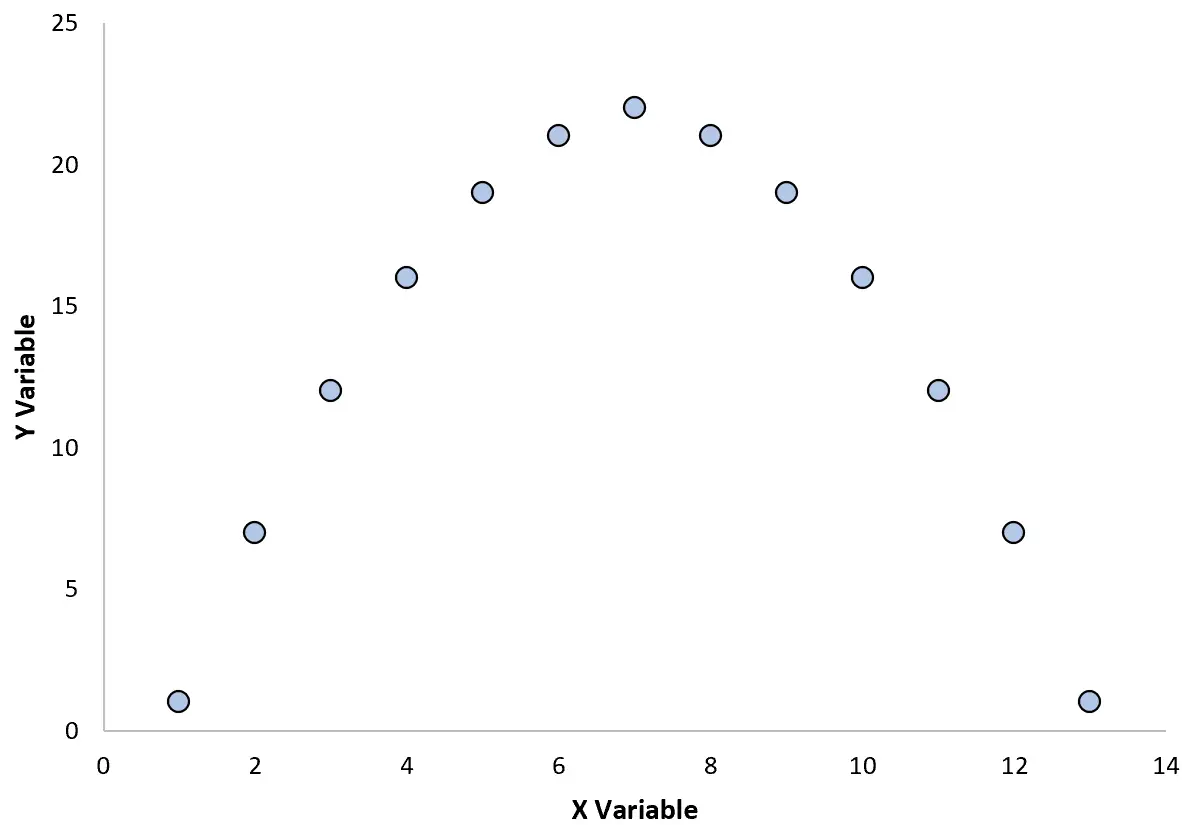
如果我们计算这两个变量之间的相关系数，结果是r = 0。这意味着两个变量之间不存在线性关系。

然而，从图中我们可以看出，这两个变量确实存在关系——只是一种二次关系，而不是线性关系。

因此，在计算两个变量之间的相关性时，请记住，创建散点图来可视化变量之间的关系也很有用。

即使两个变量不具有线性关系，它们也可能具有非线性关系，并在散点图中显示出来。

其他资源

以下教程更详细地解释了如何在不同情况下使用相关性：

6个现实生活中的相关性例子
什么被认为是“强”相关性？
相关性对比协会：有什么区别？
相关与回归：有什么区别？