什么是开放式发行版？

在统计学中，开放分布是一种频率分布，其中一个或多个类（或“箱”）是开放的。

例如，以下频率分布表示开放分布，其中最小类是开放的：

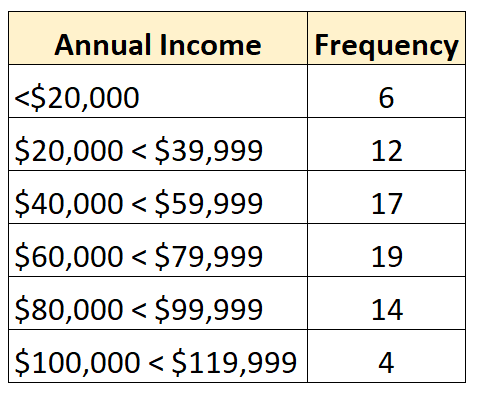
下面的频率分布显示了一个开放分布，其中最大的类是开放的：

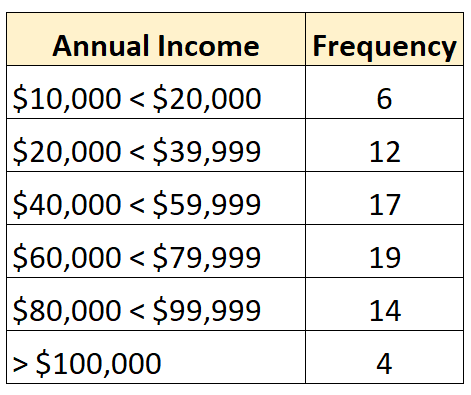
相反，封闭分布是每个类别的频率分布都有上限和下限的分布，如下所示：

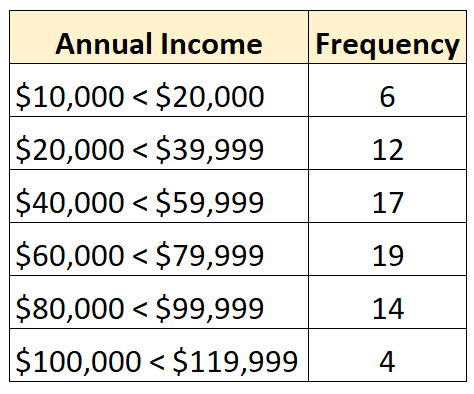
是什么导致开放分布？

开放分布通常是研究人员选择以其中一类最终开放的方式收集数据的结果。

例如，假设研究人员对某个城市的居民进行调查，询问他们的家庭年收入。

研究人员可能会选择给出最广泛的答案“100,000 美元”，因为他们知道，如果收入明显高于 100,000 美元，高收入居民可能不愿意分享他们的收入。

相反，研究人员可能会选择给出尽可能简短的答案，因为他或她知道收入很少的居民也不愿意分享他们的收入。

简而言之，研究人员经常在调查中加入开放课程，因为他们希望最大限度地增加愿意回答调查问题的人数。

开放发行版的问题

开放分布的问题在于真实数据受到审查。换句话说，我们可以知道某个城市有多少人收入超过10万美元，但我们实际上并不知道他们的确切年收入。

有可能有些人的收入为 150,000 美元、250,000 美元、500,000 美元甚至更多，但我们不知道，因为这些人在“调查”中无法表明他们的收入“>100,000 美元”。

由于数据在开放分布中被审查，我们也无法计算数据集中值的精确平均值和标准差，因为我们无法访问原始数据中的所有值。

如何分析开放分布

由于我们无法计算开放分布的精确均值，因此我们经常使用中位数作为数据集“中心”的度量。

回想一下，中位数代表数据集的中间值。

当使用开放分布时，我们可以使用以下公式来找到中位数的最佳估计：

中位数的最佳估计： L + ((n/2 – F) / f) * w

金子：

• L：中间组的下限
• n：观察总数
• F:到中间组的累积频率
• f：中间组的频率
• w：中间组的宽度

例如，假设我们有以下开放发行版：

数据集中共有72个值。因此，我们知道中值将位于数据集中第 36 个和第 37 个最大值之间。每个值都属于“60,000 美元 – 79,999 美元”类别，因此我们知道收入中位数在该范围内。

我们对中位数的最佳估计是：

中位数：60,000 + ((72/2 – 25) / 19) * 19,999 = $71,578

该值代表了我们对该数据集中个人年收入中位数的最佳估计。