如何在 ti-84 计算器上使用 geometpdf() 和 geometcdf()
几何分布描述了在一系列试验中经历第一次成功之前经历一定次数的失败的概率,具有以下特征:
- 只有两种可能的结果:成功或失败。
- 每次试验的成功概率是相同的。
如果随机变量X服从几何分布,则在经历第一次成功之前经历k 次失败的概率可以通过以下公式求出:
P(X=k) = (1-p) kp
金子:
- k:第一次成功之前的失败次数
- p:每次试验成功的概率
可以使用以下公式找到在第一次成功之前经历k 次或更少失败的累积概率:
P(X≤k) = 1 – (1-p) k+1
要在 TI-84 计算器上计算与几何分布相关的概率,您可以使用以下函数:
- geometpdf(概率,测试)
- geometcdf(概率,测试)
以下示例展示了如何在实践中使用每个函数。
示例 1:如何使用 geometpdf()
假设一名研究人员在图书馆外等候,询问人们是否支持某项法律。某个人支持该法律的概率为 p = 0.2。与研究人员交谈的第四个人第一个支持该法律的概率有多大?
为了回答这个问题,我们可以使用geometpdf()函数。
按2nd ,然后按VARS 。滚动到geometpdf()并按ENTER 。
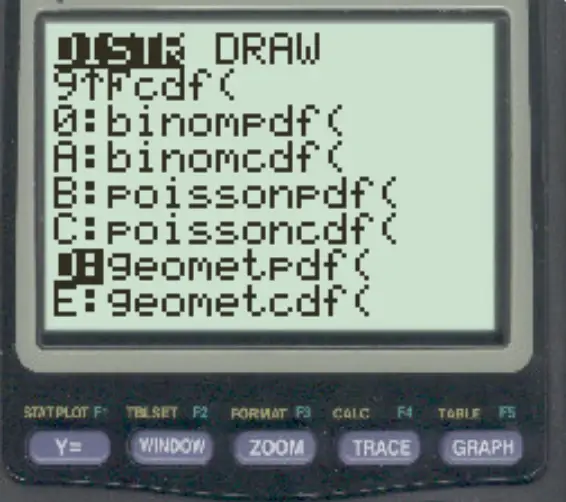
然后输入以下值并按ENTER 。
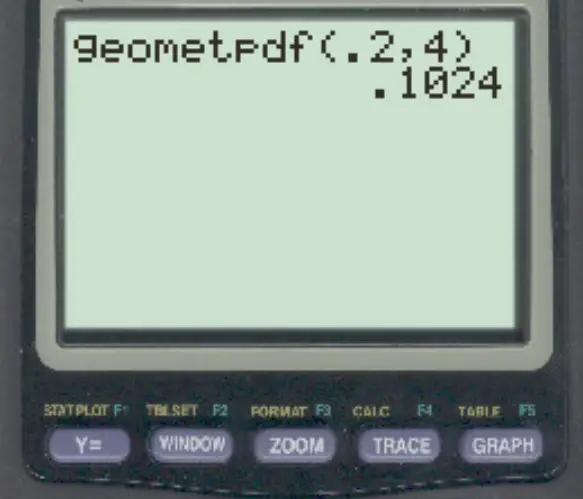
与研究人员交谈的第四个人是第一个支持该定律的概率是0.1024 。
示例 2:如何使用 geometcdf()
假设我们知道有 4% 的人拜访某个银行家是为了宣告破产。银行家在遇到宣布破产的人之前遇到的人少于 9 人的概率是多少?
为了回答这个问题,我们可以使用geometcdf()函数。
按2nd ,然后按VARS 。向下滚动到geometcdf()并按ENTER 。
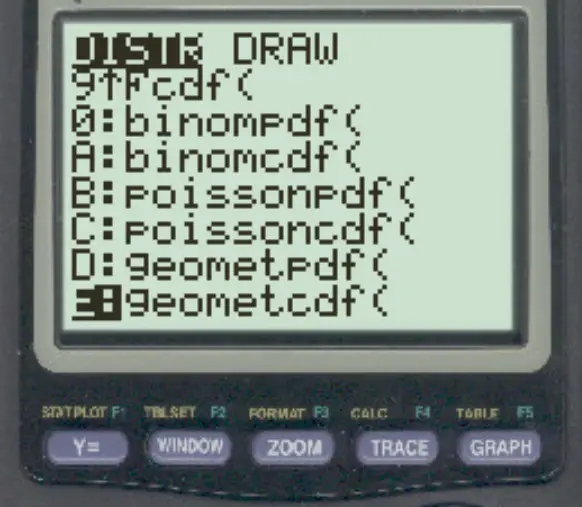
然后输入以下值并按ENTER 。
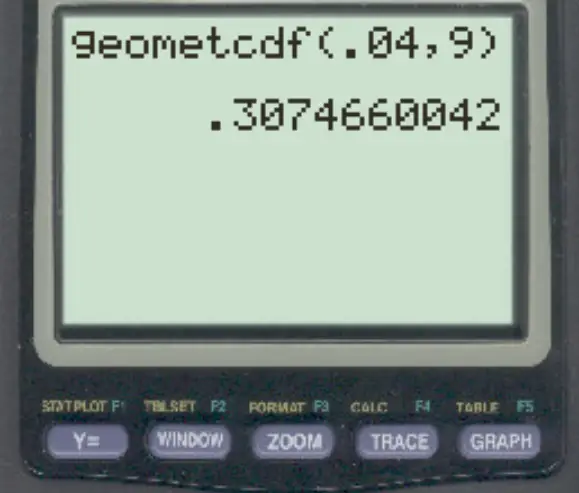
银行家在遇到宣布破产的人之前遇到的人少于 9 人的概率是0.307466 。
奖励:随意使用这个在线几何分布计算器来确认您的结果。
其他资源
如何在 TI-84 计算器上计算正态概率
如何在 TI-84 计算器上计算二项式概率
如何在 TI-84 计算器上计算泊松概率