几何分布简介

几何分布描述了在一系列伯努利试验中经历第一次成功之前经历一定次数的失败的概率。

伯努利试验是一种只有两种可能结果的实验——“成功”或“失败”——并且每次进行实验的成功概率都是相同的。

伯努利文章的一个例子是抛硬币。硬币只能落在两个正面上（我们可以将正面称为“命中”，反面称为“失败”），并且假设硬币是公平的，每次翻转成功的概率为 0.5。

如果随机变量X服从几何分布，则在经历第一次成功之前经历k 次失败的概率可以通过以下公式求出：

P(X=k) = (1-p) ^kp

金子：

• k：第一次成功之前的失败次数
• p：每次试验成功的概率

例如，假设我们想知道必须掷一枚公平的硬币多少次才能出现正面。我们可以使用上面的公式来确定经历 0、1、2、3 次故障等的概率。在硬币落在正面之前：

注意：如果硬币第一次抛掷时正面朝上，则“失败”次数为 0。

P(X=0) = (1-.5) ⁰ (.5) = 0.5

P(X=1) = (1-.5) ¹ (.5) = 0.25

P(X=2) = (1-.5) ² (.5) = 0.125

P(X=3) = (1-0.5) ³ (0.5) = 0.0625

我们可以计算任意次数的硬币抛掷的概率，直到无穷大。然后我们创建一个简单的直方图来可视化该概率分布：

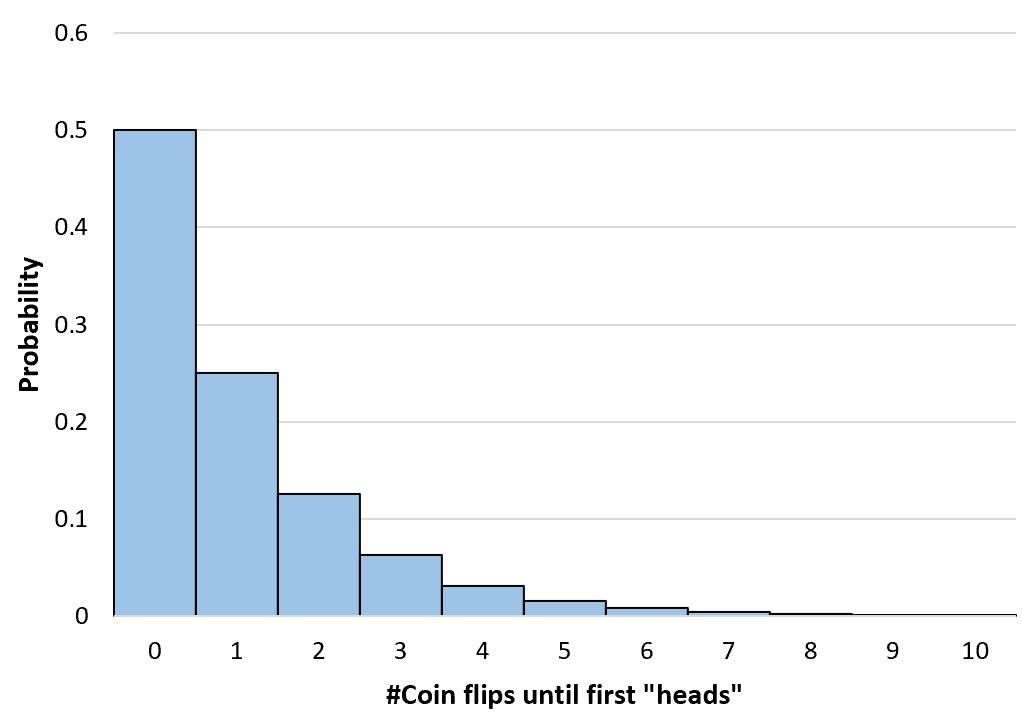
累积几何概率的计算

我们经历 k 次或更少的失败直到第一次成功的累积概率可以通过以下公式找到：

P(X≤k) = 1 – (1-p) ^k+1

金子：

• k：第一次成功之前的失败次数
• p：每次试验成功的概率

例如，假设我们想知道硬币最终正面朝上之前“未命中”三次或更少的概率。我们将使用以下公式来计算该概率：

P(X≤3) = 1 – (1-0.5) ³⁺¹ = 0.9375

我们可以使用类似的公式计算每个累积概率：

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0.5

P(X≤1) = 1 – (1-0.5) ¹⁺¹ = 0.75

P(X≤2) = 1 – (1-0.5) ²⁺¹ = 0.875

我们可以计算任意次数的累积概率，直到无穷大。然后我们可以创建一个直方图来可视化这个累积概率分布：

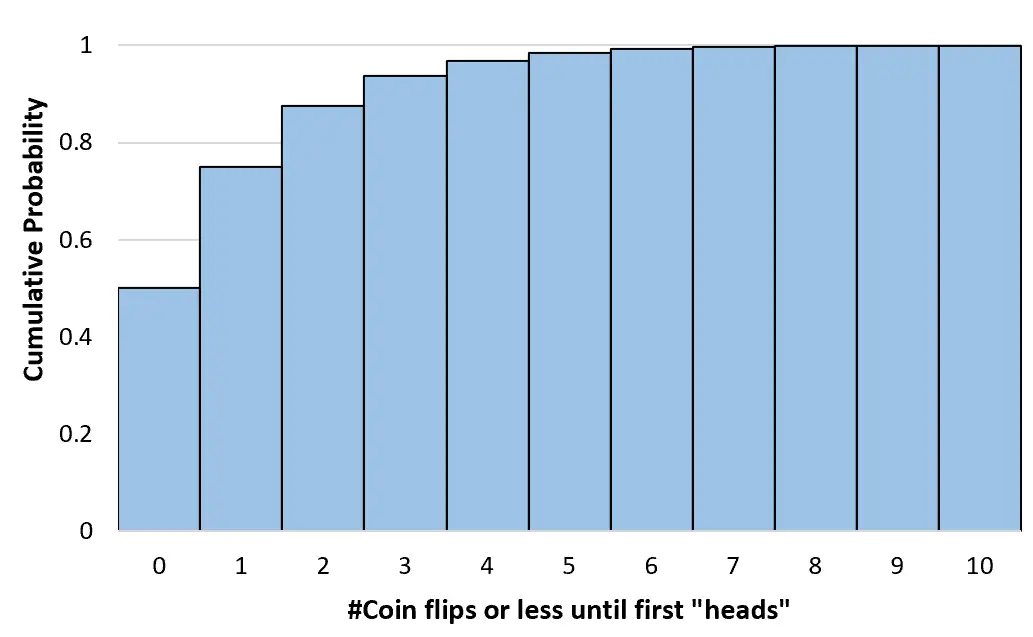
几何分布的性质

几何分布具有以下性质：

分布的平均值为(1-p) / p 。

分布的方差为(1-p) / p ² 。

例如：

我们预计硬币在反面落地之前正面朝上的平均次数为 (1-p) / p = (1-.5) / .5 = 1 。

直到正面朝上为止的抛掷次数的方差为 (1-p)/ ^p2 =(1-.5)/。 ⁵² = 2 。

几何分布练习题

使用以下练习题来测试您对几何分布的了解。

注意：我们将使用几何分布计算器来计算这些问题的答案。

问题1

问题：一名研究人员在图书馆外等候，询问人们是否支持某项法律。某个人支持该法律的概率为 p = 0.2。与研究人员交谈的第四个人第一个支持该法律的概率有多大？

答案：直到第一次成功为止的“失败”次数，即在第一个人支持该法律之前不支持该法律的人数为 3。因此，在使用 p = 0.2 和 x 的几何分布计算器时= 3 次失败，我们发现 P(X=3) = 0.10240 。

问题2

问题：一名研究人员在图书馆外等候，询问人们是否支持某项法律。某个人支持该法律的概率为 p = 0.2。研究人员必须与四个以上的人交谈才能找到支持该法律的人的概率有多大？

答案：使用几何分布计算器，p = 0.2 且 x = 4 次失败，我们发现 P(X>4) = 0.32768 。

问题3

问题：一名研究人员在图书馆外等候，询问人们是否支持某项法律。某个人支持该法律的概率为 p = 0.2。在找到支持该法律的人之前，研究人员需要与多少人交谈？

答案：回想一下，几何分布的平均值是(1-p) / p 。在这种情况下，平均值将为 (1-.2) / .2 = 4 。