如何计算分类变量之间的相关性

我们经常使用皮尔逊相关系数来计算连续数值变量之间的相关性。

但是，我们需要使用不同的度量来计算分类变量之间的相关性，即采用名称或标签的变量，例如：

• 婚姻状况（单身、已婚、离婚）
• 吸烟状况（吸烟者、非吸烟者）
• 眼睛颜色（蓝色、棕色、绿色）

计算分类变量之间的相关性有三种常用的度量：

1.四相关性：用于计算二元分类变量之间的相关性。

2. 多相关性：用于计算序数分类变量之间的相关性。

3. Cramer’s V：用于计算名义分类变量之间的相关性。

以下部分提供了如何计算这三个测量值中每一个的示例。

指标 1：四面相关性

四相关性用于计算二元分类变量之间的相关性。请记住，二元变量是只能采用两个可能值之一的变量。

四向相关性取值范围为-1~1，其中-1表示强负相关，0表示无相关，1表示强正相关。

例如，假设我们想知道性别是否与对政党的偏好相关。因此，我们对 100 名选民进行了简单的随机抽样，并询问他们对某个政党的偏好。

下表列出了调查结果：

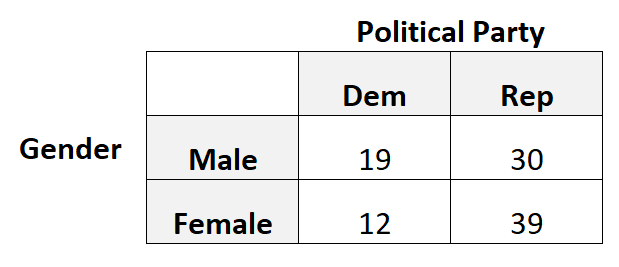
在这种情况下，我们将使用四相关性，因为每个分类变量都是二元的，也就是说，每个变量只能采用两个可能的值。

我们可以在R中使用以下代码来计算两个变量之间的四向相关性：

 library (psych)

#create 2x2 table
data = matrix(c(19, 12, 30, 39), nrow= 2 )

#view table
data

#calculate tetrachoric correlation
tetrachoric(data)

tetrachoric correlation 
[1] 0.27

四面相关性结果为0.27 。这个值相当低，表明性别和政党偏好之间的关联很弱（如果有的话）。

指标 2：多元相关性

多相关性用于计算序数分类变量之间的相关性。回想一下，序数变量是其可能值具有自然顺序的变量。

多向相关性取值范围为-1到1，其中-1表示强负相关，0表示无相关，1表示强正相关。

例如，假设您想知道两个不同的电影评级机构的电影评级之间是否具有高度相关性。

我们要求每个机构按照 1 到 3 的等级对 20 部不同的电影进行评分，其中 1 表示“差”，2 表示“差”，3 表示“好”。

下表显示了结果：

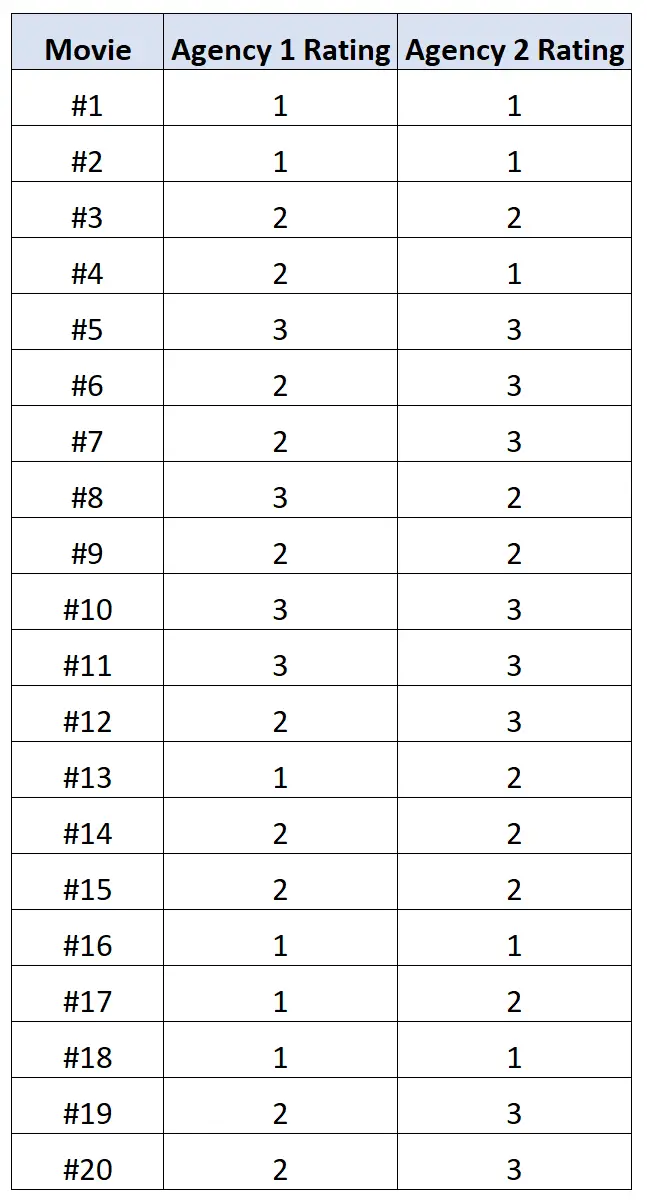
我们可以在 R 中使用以下代码来计算两个机构评级之间的多向相关性：

 library (polycor)

#define movie ratings
x <- c(1, 1, 2, 2, 3, 2, 2, 3, 2, 3, 3, 2, 1, 2, 2, 1, 1, 1, 2, 2)
y <- c(1, 1, 2, 1, 3, 3, 3, 2, 2, 3, 3, 3, 2, 2, 2, 1, 2, 1, 3, 3)

#calculate polychoric correlation between ratings
polychor(x, y)

[1] 0.7828328

多向相关性结果为0.78 。这个值相当高，表明每个机构的评级之间存在很强的正相关关系。

指标 3：克莱默 V

Cramer’s V用于计算名义分类变量之间的相关性。请记住，名义变量是带有类别标签但没有自然顺序的变量。

Cramer’s V 的取值范围为 0 到 1，其中 0 表示变量之间没有关联，1 表示变量之间有强关联。

例如，假设我们想知道眼睛颜色和性别之间是否存在相关性。因此，我们询问了 50 个人并得到以下结果：

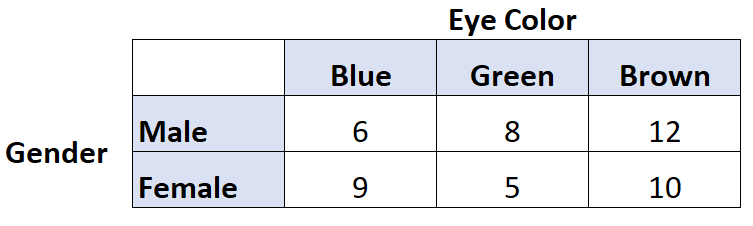
我们可以在 R 中使用以下代码来计算这两个变量的 Cramer’s V：

 library (rcompanion)

#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 )

#view table
data

     [,1] [,2] [,3]
[1,] 6 8 12
[2,] 9 5 10

#calculate Cramer's V
cramerV(data)

Cramer V 
  0.1671

Cramer 的 V 结果为0.1671 。该值相当低，表明性别和眼睛颜色之间的关联较弱。

其他资源

皮尔逊相关系数简介
四面相关简介
分类变量或定量变量：有什么区别？
测量级别：名义、序数、间隔和比率