如何查找分组数据的中位数：举例
我们经常想要计算以某种方式分组在一起的数据的中位数。
回想一下，当所有值从小到大排序时，中位数表示直接位于数据集中间的值。
例如，假设我们有以下分组数据：
尽管由于我们不知道原始数据值而无法计算准确的中位数，但可以使用以下公式估计中位数：
分组数据的中位数 = L + W[(N/2 – C) / F]
金子：
- L : 中位等级的下限
- W ：中位类宽度
- N : 总频率
- C ：达到中位类别的累积频率
- F : 中位班级频率
注意：中间类是包含位于 N/2 的值的类。在上面的示例中，总共有 N = 23 个值。因此，中位值为 23/2 = 11.5，属于 21-30 级。
以下示例展示了如何计算不同场景下分组数据的中位数。
示例 1：计算分组数据的中位数
假设我们有以下频率分布，显示某个班级 40 名学生的考试评分：
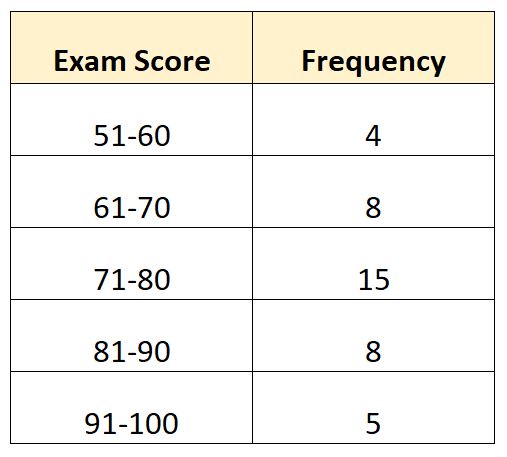
在此示例中，总共有 N = 40 个值。因此，中值位于 40/2 = 20 所在的类别中。第 20 大值将在71-80类中。
知道了这一点，我们可以计算出以下值：
- L : 中产阶级下限： 71
- W ：中位类宽度： 9
- N ：总频率： 40
- C ：达到中位等级的累积频率： 12
- F : 中位数班级频率： 15
我们可以将这些值代入公式来计算分布的中位数：
- 中位数 = L + W[(N/2 – C) / F]
- 中位数 = 71 + 9[(40/2 – 12) / 15]
- 中位数 = 75.8
我们估计考试成绩中位数为75.8 分。
示例 2：计算分组数据的中位数
假设我们有以下频率分布，显示 60 名篮球运动员每场比赛的得分数：
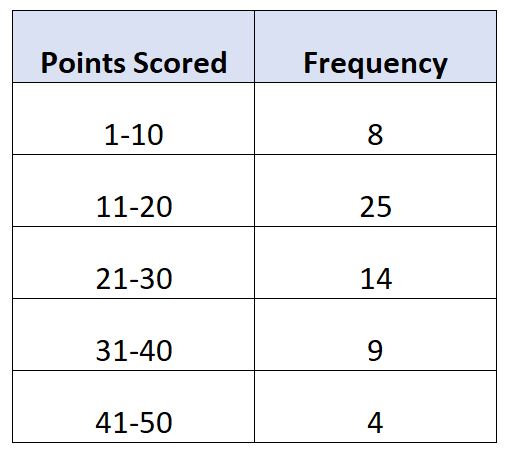
在此示例中，总共有 N = 60 个值。因此，中值位于 60/2 = 30 所在的类别中。第 30 大值将位于11-20类中。
知道了这一点，我们可以计算出以下值：
- L : 中产阶级下限： 11
- W ：中位类宽度： 9
- N ：总频率： 60
- C : 达到中位等级的累积频率： 8
- F : 中位数班级频率： 25
我们可以将这些值代入公式来计算分布的中位数：
- 中位数 = L + W[(N/2 – C) / F]
- 中位数 = 11 + 9[(60/2 – 8) / 25]
- 中位数 = 18.92
我们估计考试成绩中位数为18.92 分。
其他资源
以下教程说明如何对分组数据执行其他常见操作：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多