如何计算分组数据的四分位数
四分位数是将数据集分为四个相等部分的值。
您可以使用以下公式计算分组数据的四分位数：
Q i = L + (C/F) * (iN/4 – M)
金子：
- L ：包含第 i个四分位数的区间下限
- C ：类的宽度
- F ：包含第 i 个四分位数的区间的频率
- N : 总频率
- M ：导致包含第 i个四分位数的区间的累积频率
下面的例子展示了如何在实践中使用这个公式。
示例：计算分组数据的四分位数
假设我们有以下频率分布：
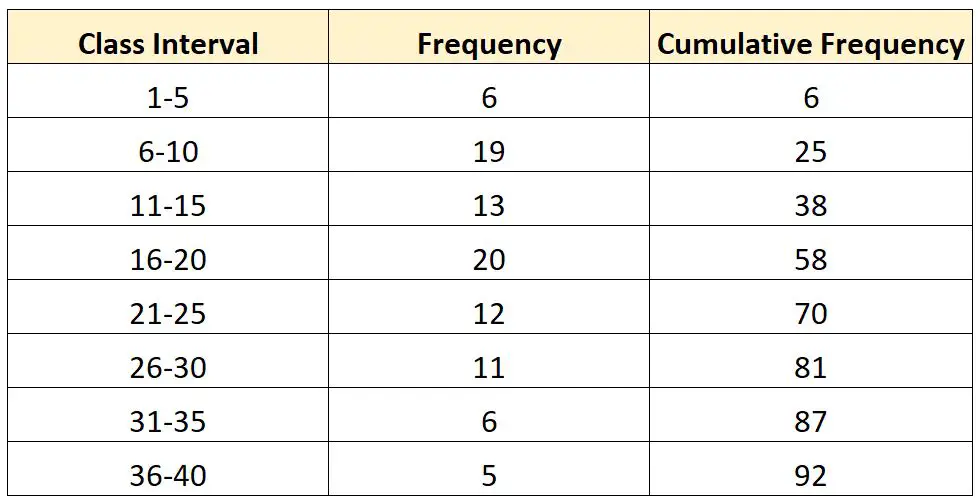
现在假设我们要计算该分布的第三个四分位数 (Q 3 ) 处的值。
第三个四分位数的值将位于分布中的位置 (iN/4)。
因此，(iN/4) = (3*92/4) = 69。
包含第三个四分位数的区间将是区间21-25 ，因为 69 位于 58 和 70 的累积频率之间。
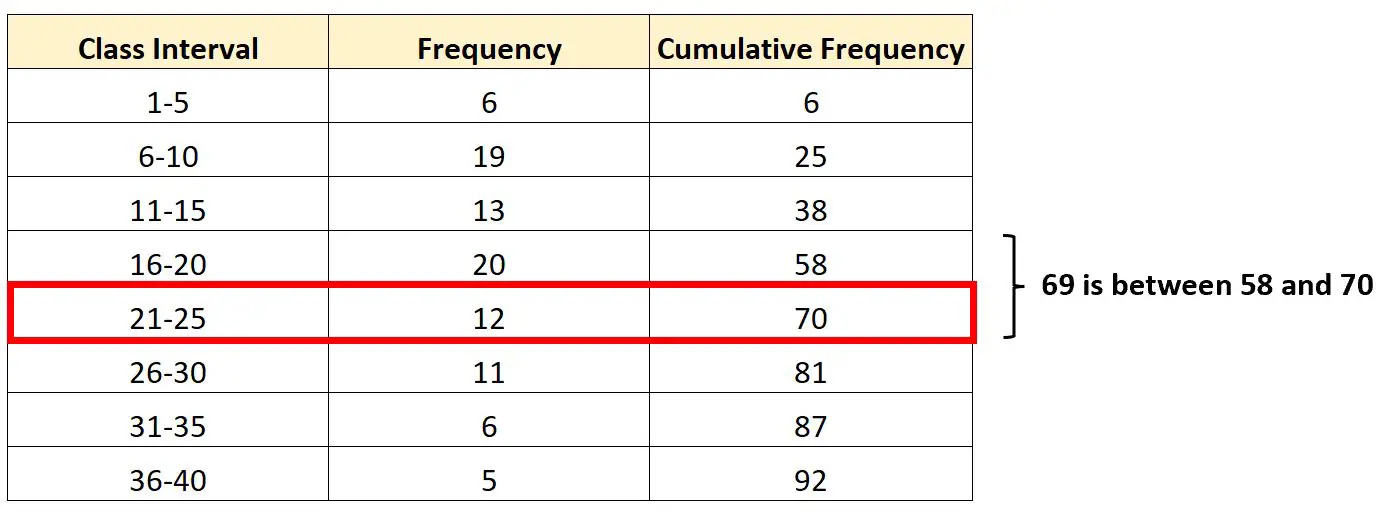
知道了这一点，我们就可以找到每个必要的值来代入我们的公式：
L ：包含第 i个四分位数的区间下限
- 间隔的下限为21 。
C ：类的宽度
- 类的宽度计算如下： 25 – 21 = 4 。
F ：包含第 i 个四分位数的区间的频率
- 21-25类的频率为12
N : 总频率
- 表中总累积频率为92 。
M ：导致包含第 i个四分位数的区间的累积频率
- 到21-25级的累计频率为58 。
然后我们可以将所有这些值代入前面的公式中以找到第三个四分位数的值：
- Q i = L + (C/F) * (iN/4 – M)
- Q 3 = 21 + (4/12) * ((3)(92)/4 – 58)
- Q3 = 24.67
第三个四分位数的值为24.67 。
您可以使用类似的方法来计算第一和第二四分位数值。
其他资源
以下教程提供了有关使用分组数据的更多信息：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多