如何查找分组数据的方差（带有示例）
我们经常想要计算分组频率分布的方差。
例如，假设我们有以下分组频率分布：
尽管由于我们不知道原始数据值而无法计算精确的方差，但可以使用以下公式估计方差：
方差： Σn i (m i -μ) 2 / (N-1)
金子：
- n i :第i组的频率
- mi :第 i组的中间
- μ ：平均值
- N：总样本量
注：每组的中点可以通过取范围下限值和上限值的平均值来找到。例如，第一组的中点计算如下：(1+10)/2=5.5。
下面的例子展示了如何在实践中使用这个公式。
示例：计算分组数据的方差
假设我们有以下分组数据：
以下是我们如何使用前面提到的公式来计算分组数据的方差：
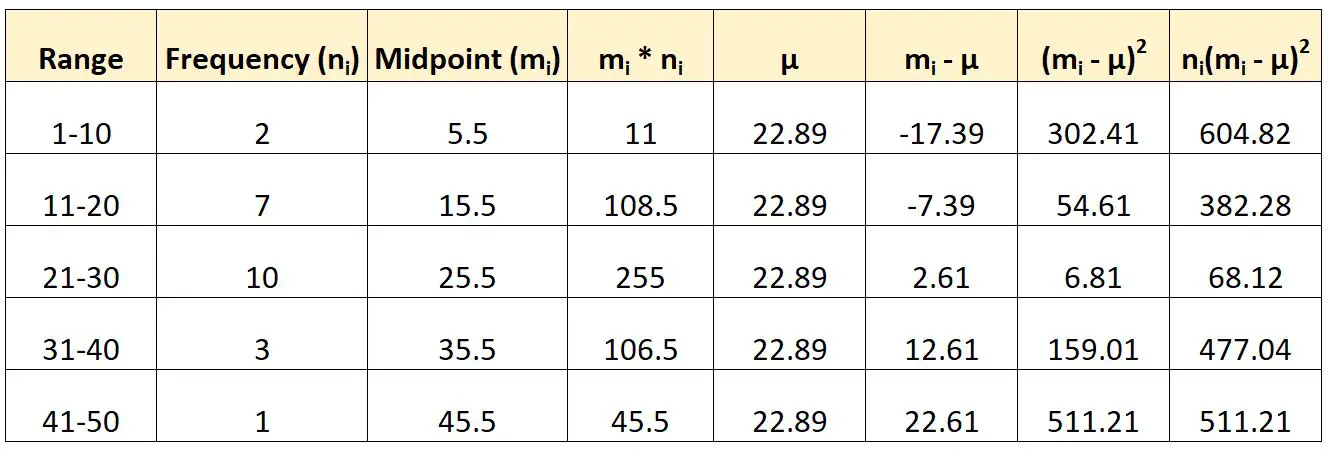
然后我们将计算方差如下：
- 方差： Σn i (m i -μ) 2 / (N-1)
- 差值：(604.82 + 382.28 + 68.12 + 477.04 + 511.21) / (23-1)
- 差值：92.885
数据集的方差为92.885 。
其他资源
以下教程解释了如何计算分组数据的其他指标：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多