如何查找分组数据的范围：举例
我们经常想要计算以某种方式分组在一起的数据的范围。
请记住，极差代表数据集中最大值和最小值之间的差异。
例如，假设我们有以下分组数据：
尽管由于我们不知道原始数据值而无法计算准确的范围，但可以使用以下公式之一来估计范围：
公式1：使用上限和下限
分组数据范围 = U max – L min
金子：
- U : 最大间隔的上限
- L : 最小间隔的下限
公式 2：使用中点
分组数据范围 =最大中点 –最小中点
金子：
- Max Mid : 最大间隔的中点
- Middle min : 最小间隔的中点
以下示例展示了如何在实践中使用每个公式。
示例1：计算分组数据范围
假设我们有以下频率分布，显示某个班级 40 名学生的考试评分：
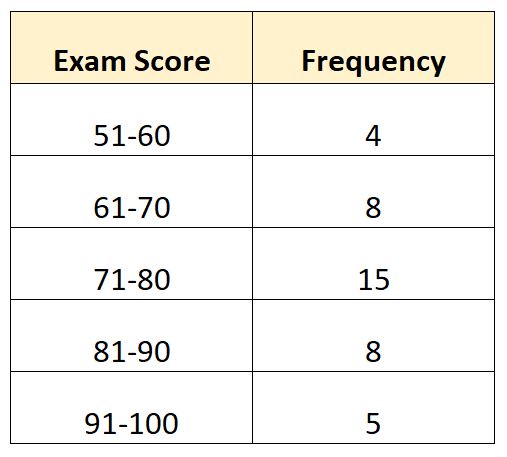
以下是如何使用每个公式计算分组数据的范围：
公式1：使用上限和下限
- 分组数据范围 = U max – L min
- 分组数据范围 = 100 – 51
- 分组数据范围 = 49
使用这个公式，我们估计范围为49 。
公式 2：使用中点
- 分组数据范围 =最大中点 –最小中点
- 分组数据范围 = (100+91)/2 – (60+51)/2
- 分组数据范围 = 95.5 – 55.5
- 分组数据范围 = 40
使用此公式，我们估计范围为40 。
示例2：计算分组数据范围
假设我们有以下频率分布，显示 60 名篮球运动员每场比赛的得分数：
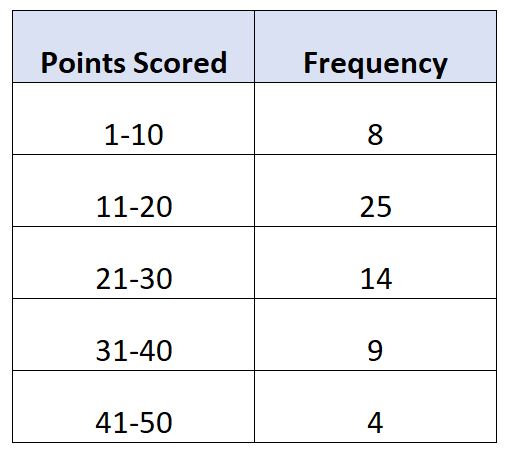
以下是如何使用每个公式计算分组数据的范围：
公式1：使用上限和下限
- 分组数据范围 = U max – L min
- 分组数据范围 = 50 – 1
- 分组数据范围 = 49
使用这个公式，我们估计范围为49 。
公式 2：使用中点
- 分组数据范围 =最大中点 –最小中点
- 分组数据范围 = (50+41)/2 – (1+10)/2
- 分组数据范围 = 45.5 – 5.5
- 分组数据范围 = 40
使用此公式，我们估计范围为40 。
其他资源
以下教程说明如何对分组数据执行其他常见操作：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多