分配功能

经过本杰明·安德森博 8月 5, 2023 可能性 0 条评论

在本文中，您将找到分布函数的说明、其值的计算方式以及分布函数的实际示例。此外，您将能够看到分布函数和密度函数之间的差异。

什么是分布函数？

分布函数也称为累积分布函数，是表示分布的累积概率的数学函数。也就是说，任何值的分布函数的图像都等于该变量取该值或更低值的概率。

累积分布函数也可以用缩写 FDA 来指代，尽管其通常的符号是大写 F。

因此，分布函数由以下公式定义：

$F(x)=P[X\leq x]$

如何计算分布函数

然后我们解释如何根据概率分布是离散的还是连续的来计算分布函数的值。

谨慎的盒子

如果随机变量是离散的，则累积分布函数等于所有等于或小于x的值的概率之和。

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

金子

$f(u)$

是与离散变量相关的概率函数。

续案

如果随机变量是连续的，则累积分布函数相当于密度函数从负无穷大到相关值的积分。

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

金子

$f(u)$

是与连续变量相关的密度函数。

分布函数示例

现在我们知道了分布函数的定义，让我们看一个实际的分步示例来学习如何计算分布函数值。

计算抛硬币四次的随机实验的分布函数。

要解决这个练习，您必须首先计算与四次抛硬币期间获得的正面朝上的次数相关的所有概率：

因此，由于它是离散变量，为了确定分布函数的图像，将概率添加到相关变量的值就足够了：

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

因此，抛掷四枚独立硬币的翻转头分布函数的值如下：

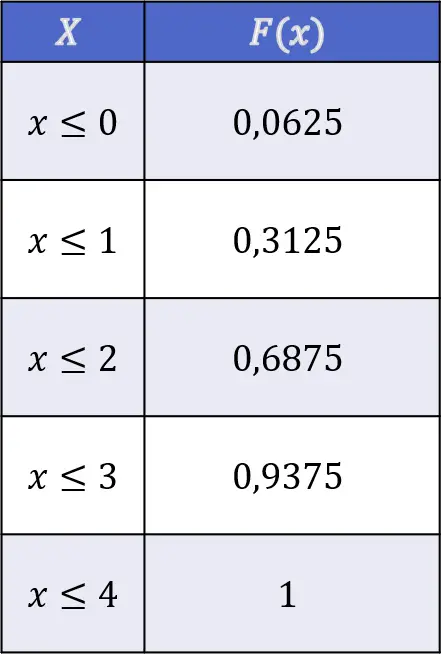
分布函数的性质

无论变量的类型如何，分布函数始终具有以下属性：

累积分布函数的值在 0 和 1 之间（含 0 和 1）。

$0\leq F(x) \leq 1$

当x趋于无穷大时，分布函数的极限等于 1。

$\displaystyle\lim_{x\to +\infty} F(x)=1$

另一方面，当x接近负无穷大时，分布函数的极限为零。

$\displaystyle\lim_{x\to -\infty} F(x)=0$

就其特征而言，分布函数是单调且非递减的。

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

此外，如果
$a\leq b$

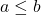
满足以下方程。

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

分布函数和密度函数

最后，我们将了解分布函数和密度函数之间的区别，因为这两个统计概念经常被混淆。

分布函数和密度函数之间的区别在于它们定义的概率类型。密度函数描述了变量取某一值的概率，而分布函数描述了变量的累积概率。

即分布函数用于计算变量等于或小于某个值的概率。

请注意，密度函数仅指连续变量，因此只有当所研究的变量是连续的时，这种区别才有意义。

请注意，与服从平均值为 1、标准差为 0.5 的正态分布的变量的密度函数相比，分布函数的图形表示有何变化：

要了解有关密度函数的更多信息，请参阅以下文章：

➤参见：密度函数

关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多