如何在 ti-84 计算器上使用 invnorm（附示例）

您可以使用 TI-84 计算器上的invNorm()函数来查找与正态分布相关的 z 临界值。

该函数使用以下语法：

invNorm(概率, μ, σ)

金子：

• 概率：显着性水平
• μ：总体平均值
• σ：总体标准差

您可以通过按2nd然后按VARS在 TI-84 计算器上访问此功能。这将带您进入DISTR屏幕，然后您可以在其中使用invNorm() ：

以下示例展示了如何在实践中使用此功能。

示例 1：单侧测试的临界 Z 值

假设研究人员使用 α = 0.05 进行左手假设检验。与该 alpha 级别相对应的 z 临界值是多少？

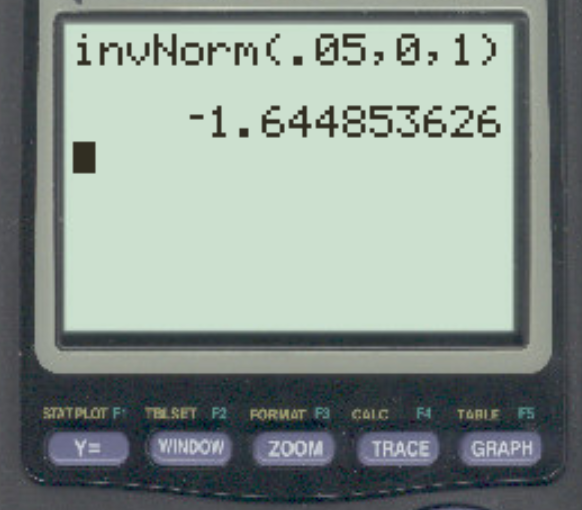
答案是 z = -1.64485 。

假设研究人员使用 α = 0.05 进行直接假设检验。与该 alpha 级别相对应的 z 临界值是多少？

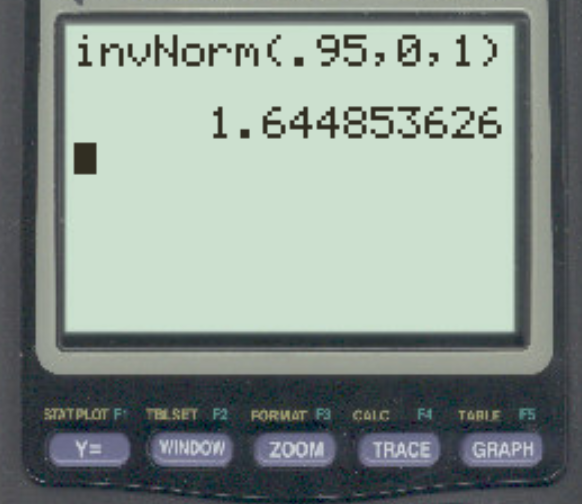
答案是 z = 1.64485 。

示例 2：双面测试的临界 Z 值

假设研究人员使用 α = 0.05 进行双尾假设检验。与该 alpha 级别相对应的 z 临界值是多少？

为了找到这个临界值，我们可以使用公式 1 – α/2。在本例中，我们将使用 1 – 0.05/2 = 0.975 作为概率：

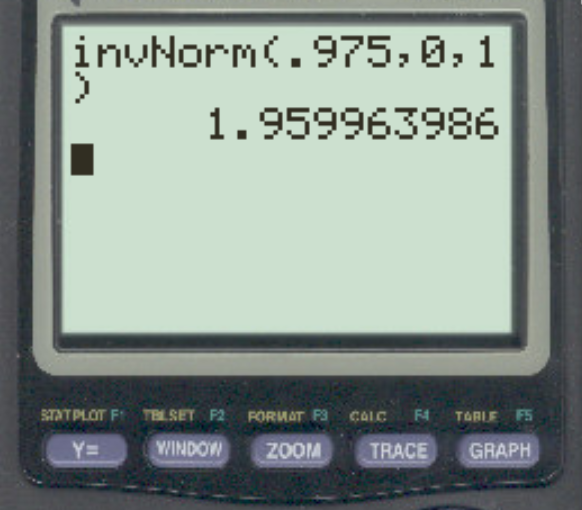
答案是 z = 1.96 。

示例 3：截止分数的临界 Z 值

假设某项考试的分数呈正态分布，平均值为 70，标准差为 8。什么分数将前 10% 的学生与其余的学生区分开来？

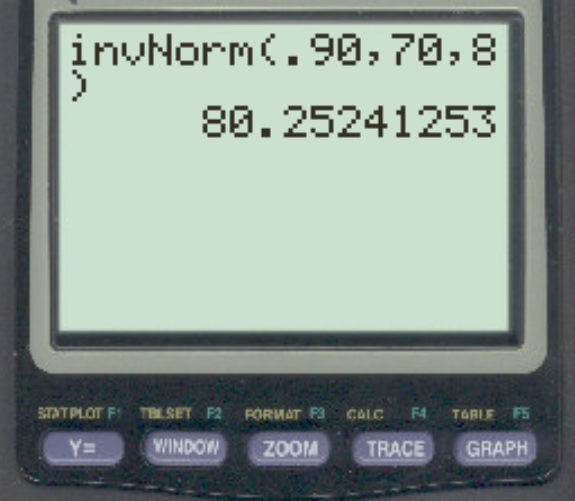
答案是80.25 。

假设某个特定城市的男性身高呈正态分布，平均值为 68 英寸，标准差为 4 英寸。底部 25% 的人与其他人的差距有多高？

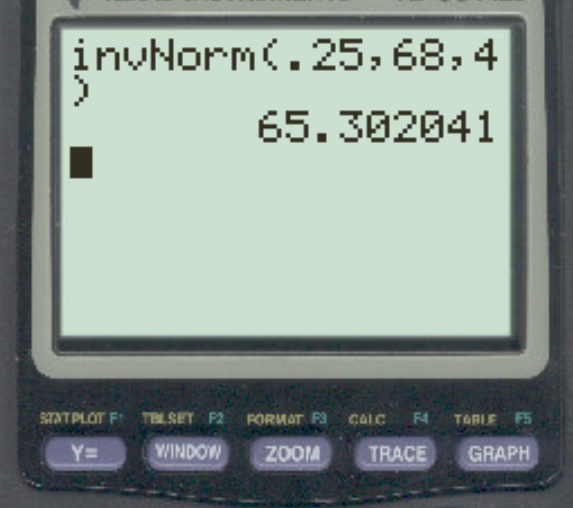
答案是65.3英寸。

其他资源

如何在 TI-84 计算器上计算二项式概率
如何在 TI-84 计算器上计算泊松概率
如何在 TI-84 计算器上计算几何概率