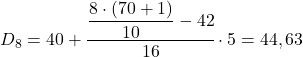十分位数

在本文中，我们将解释什么是十分位数以及它们是如何计算的。您还将找到几个已解决的十分位数计算的分步示例，此外，您还可以使用在线计算器计算任何统计样本的十分位数。

什么是十分位数？

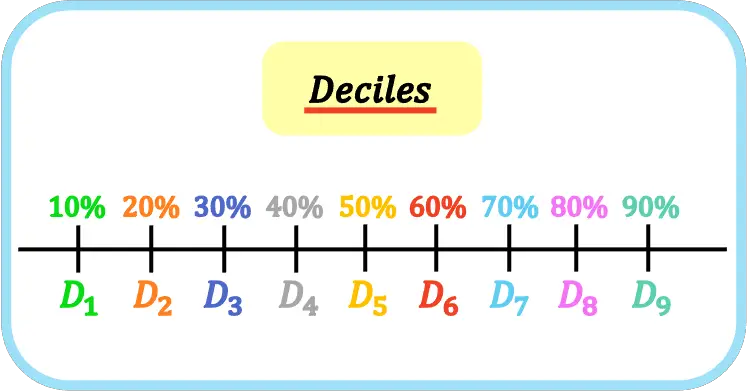
在统计学中，十分位数是将一组有序数据分为十个相等部分的九个值。因此，第一、第二、第三……十分位数代表样本或总体的 10%、20%、30%……。

例如，第四个十分位数值高于数据的 40%，但低于其余数据。

十分位数由大写字母 D 和十分位数索引表示，即第一个十分位数为 D ₁ ，第二个十分位数为 D ₂ ，第三个十分位数为 D ₃ ，依此类推。

👉您可以使用下面的计算器来计算任何数据集的十分位数。

应该注意的是，十分位数与四分位数、五分位数和百分位数相同，是非中心位置的度量。您可以在我们的网站上查看每种分位数类型的含义。

此外，第五十分位数相当于中位数和第二四分位数，因为它们将整个数据集分为两个相等的部分。

如何计算十分位数

要计算一系列统计数据的十分位数位置，请将十分位数乘以数据总数加一的总和，然后将结果除以十。

因此，十分位数公式为：

请注意：这个公式告诉我们十分位数的位置，而不是十分位数的值。十分位将是位于通过公式获得的位置的数据。

然而，有时这个公式的结果会给我们一个十进制数，因此我们必须根据结果是否是十进制数来区分两种情况：

• 如果公式的结果是一个没有小数部分的数字，那么十分位就是位于上式所提供位置的数据。
• 如果公式的结果是带有小数部分的数字，则使用以下公式计算十分位数值：

其中x _i和x _i+1为第一个公式得到的数所在位置的数字， d为第一个公式得到的数的小数部分。

现在您可能认为获取统计样本的十分位数很复杂，但实际上非常简单。如果你读完下面两个例子，你一定会更加理解。

注意：科学界对于如何计算十分位数并不完全一致，因此您可以找到对其解释略有不同的统计书籍。

十分位计算示例

正如您在上面看到的，十分位数的计算取决于第一个公式给出的数字是否为小数，这就是为什么我们在下面准备了两个已解决的示例，每种情况一个。无论如何，请记住，如果您对十分位数的组成有任何疑问，可以在评论中提问。

实施例1

• 给定以下数据，从最小到最大，找到样本的第一个、第三个和第八个十分位数。

本练习中的数据已经排序，因此无需更改顺序，否则我们必须先将数据从小到大排序。

如上所述，可以找到十分位数位置的公式如下：

本练习的样本大小为 29 个观测值，因此要计算第一个十分位数的位置，您必须用 29 代替n并用 1 代替k ：

公式的结果是 3，因此第一个十分位数将位于有序列表的第三个位置，该值对应于 85。

现在我们再次应用相同的过程，但使用第三个十分位数。我们使用以下公式将k替换为 3：

因此，第三个十分位数将是第九个位置的元素，即 97。

最后，我们执行相同的过程，但在公式中放入 8 来确定第八个十分位数：

第八个十分位数将是有序数据列表的位置 24 中的数字，因此第八个十分位数是 131。

实施例2

• 根据下表中的数据，计算十分位数 4、7 和 9。

与前面的示例一样，要获取十分位数的位置，必须使用以下公式：

在本例中，样本大小为 42，因此要找到第四个十分位数的位置，必须将参数n替换为 42，将k替换为 4：

但是这次我们从公式中得到了一个十进制数，因此我们需要应用以下公式来计算精确的十分位数：

第一个公式得出的数字是 17.2，因此第四个十分位数位于给定的第十七和第十八个之间，分别为 109 和 112。因此， _xi为109， xi ₊₁为112， d为小数部分。所获得的数量，即0.2。

我们重复相同的过程来找到第七个十分位数。我们首先计算十分位的位置：

从公式中我们得到数字 30.1，这意味着十分位数将位于位置 30 和 31 之间，其值为 154 和 159。因此，精确十分位数的计算为：

最后，我们再次应用相同的方法得到第九个十分位数。我们确定十分位数的位置：

得到的数字是十进制的，在38和39之间，其位置对应于值189和196。因此十分位数9的计算是：

十分位数计算器

将统计数据集插入下面的计算器即可计算十分位数。数据必须用空格分隔，并使用句点作为小数点分隔符输入。

分组数据中的十分位数

要计算数据按区间分组时的十分位数，我们首先需要使用以下公式找到十分位数所属的区间或区间：

因此，十分位数将位于其绝对频率立即大于先前表达式中获得的数字的区间中。

一旦我们已经知道十分位数所属的区间，我们就必须应用以下公式来找到十分位数的精确值：

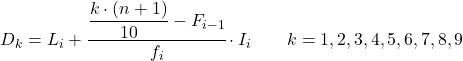
金子：

• _Li是十分位数所在区间的下限。
• n为统计数据总数。
• F _i-1是前一个间隔的累积绝对频率。
• f _i是十分位数所在区间的绝对频率。
• I _i是十分位数间隔的宽度。

为了让您了解这是如何完成的，下面您有一个完整的练习，其中计算了按间隔分组的以下数据的十分位数 3、5 和 8。

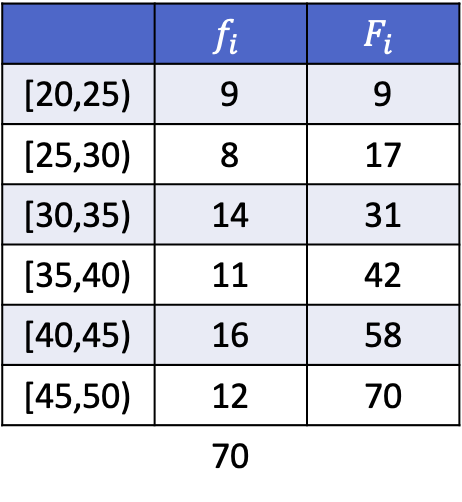
由于数据是分组的，所以每个十分位数的计算由两个步骤组成：首先找到该十分位数所在的区间，然后计算该十分位数的精确值。因此我们求出第三个十分位数的区间：

十分位数间隔将是绝对累积频率立即大于 21.3 的区间，在本例中，它是绝对累积频率为 31 的区间 [30.35)。现在我们知道了十分位数间隔，我们应用以下公式来查找十分位数的精确值：

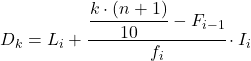
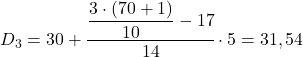
我们现在必须重新应用该方法来获得第五个十分位数。我们首先确定它所在的区间：

结果 35 意味着它在区间 [35,40) 中，但不是因为区间表达式中有 35，而是因为它的累积绝对频率 (42) 是最接近的。一旦确定了区间，我们就应用该过程的第二个公式：

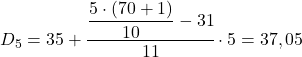
最后，我们找到第八个十分位数。为此，我们首先计算其间隔：

紧邻 56.8 之上的累积绝对频率为 58，因此第八个十分位数范围为 [40.45)。因此，确定十分位数的精确值就足够了：