统计学中什么是协变量？

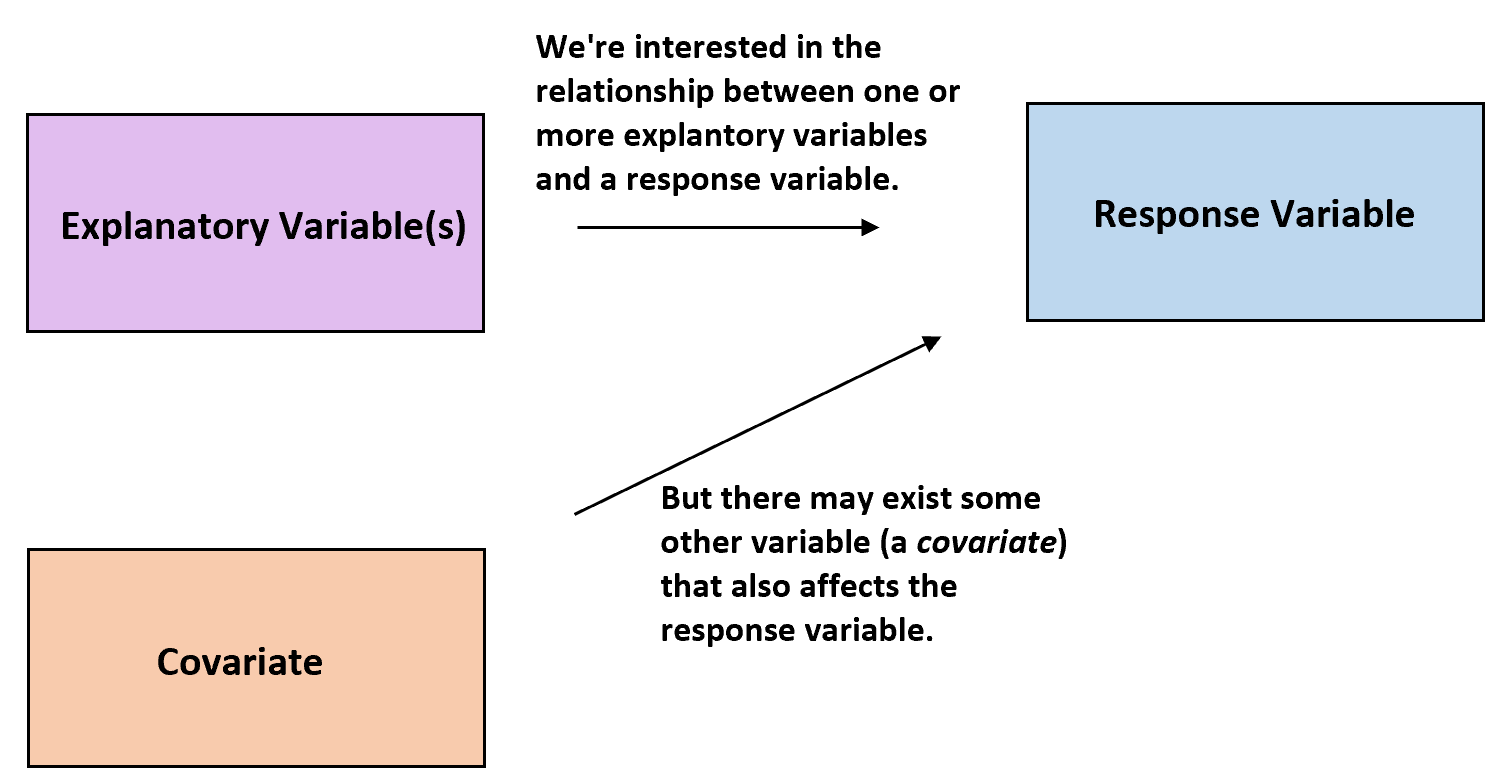
在统计学中，研究人员通常希望了解一个或多个解释变量与响应变量之间的关系。

然而，其他变量可能会影响响应变量，但研究人员并不感兴趣。这些变量称为协变量。

协变量：影响响应变量但在研究中不感兴趣的变量。

例如，假设研究人员想知道三种不同的学习方法是否会导致给定学校的平均考试成绩不同。学习技巧是解释变量，考试成绩是响应变量。

然而，这三组学生的学习能力必然存在差异。如果不考虑这一点，研究中就会出现无法解释的变化，并且更难以确定研究技术和考试结果之间的真实关系。

解释这一点的一种方法可能是使用学生当前在课堂上的成绩作为协变量。众所周知，学生当前的成绩可能与他们未来的考试表现相关。

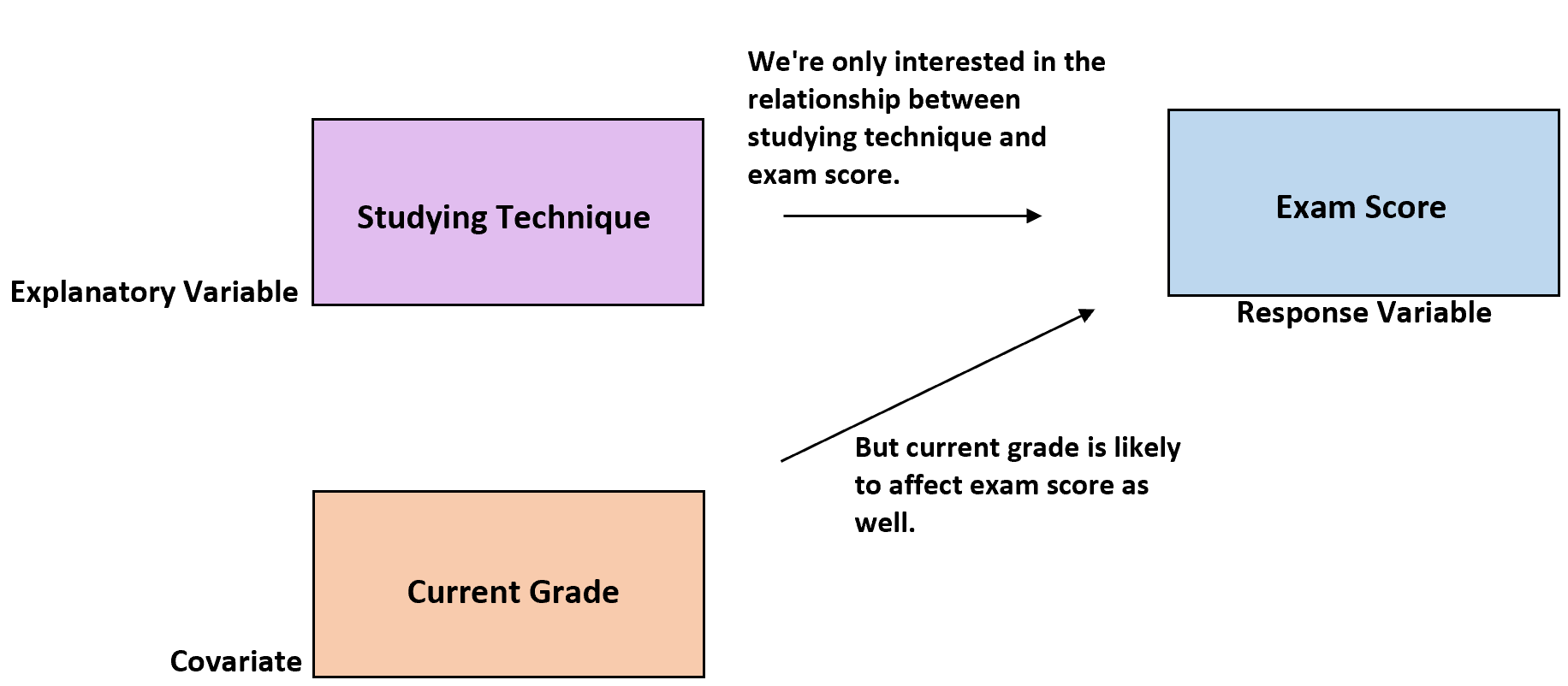
因此，尽管当前成绩不是本研究中感兴趣的变量，但它可以作为协变量包含在内，以便研究人员可以了解学习技术是否会影响考试成绩，即使在考虑了班级学生的当前成绩之后也是如此。

协变量最常出现在两种类型的环境中：ANOVA（方差分析）和回归。

方差分析中的协变量

当我们执行方差分析（无论是 单向方差分析、 双向方差分析还是更复杂的方差分析）时，我们想知道三个或更多独立组的均值之间是否存在差异。

在前面的示例中，我们想了解三种不同学习技术之间的平均考试成绩是否存在差异。为了理解这一点，我们可以进行单向方差分析。

然而，由于我们知道学生当前的成绩也可能影响考试成绩，因此我们可以将其作为协变量并执行ANCOVA （协方差分析）。

这与方差分析类似，只是我们包含一个连续变量（学生当前成绩）作为协变量，以便我们可以了解三种评分技术之间的平均考试成绩是否存在差异。学习，即使考虑到学生的成绩。当前评级。

回归中的协变量

当我们执行线性回归时，我们想要量化一个或多个解释变量与响应变量之间的关系。

例如，我们可以执行简单的线性回归来量化某个城市的平方英尺和房地产价格之间的关系。然而，众所周知，房屋的年龄也是影响房地产价格的一个变量。

特别是，老房子可能与较低的房价相关。在这种情况下，房子的年龄将是一个协变量，因为我们并不是真正有兴趣研究它，但我们知道它对房价有影响。

因此，我们可以将房屋的年龄作为解释变量，并以平方英尺和房屋的年龄作为解释变量，以房价作为响应变量进行多元线性回归。

因此，平方英尺的回归系数将告诉我们在考虑房屋的年龄后，与平方英尺增加一单位相关的房价的平均变化。

其他资源

ANCOVA（方差分析）简介
如何解释回归系数
如何在 Excel 中执行 ANCOVA
如何在 Excel 中执行多元线性回归