在现实生活中使用卡方检验的 4 个示例
在统计学中，有两种不同类型的卡方检验：
1.卡方拟合优度检验– 用于确定分类变量是否遵循假设分布。
2.卡方独立性检验– 用于确定两个分类变量之间是否存在显着关联。
在本文中，我们分享了几个示例，说明如何在现实情况中使用每种类型的卡方检验。
示例 1：卡方拟合优度检验
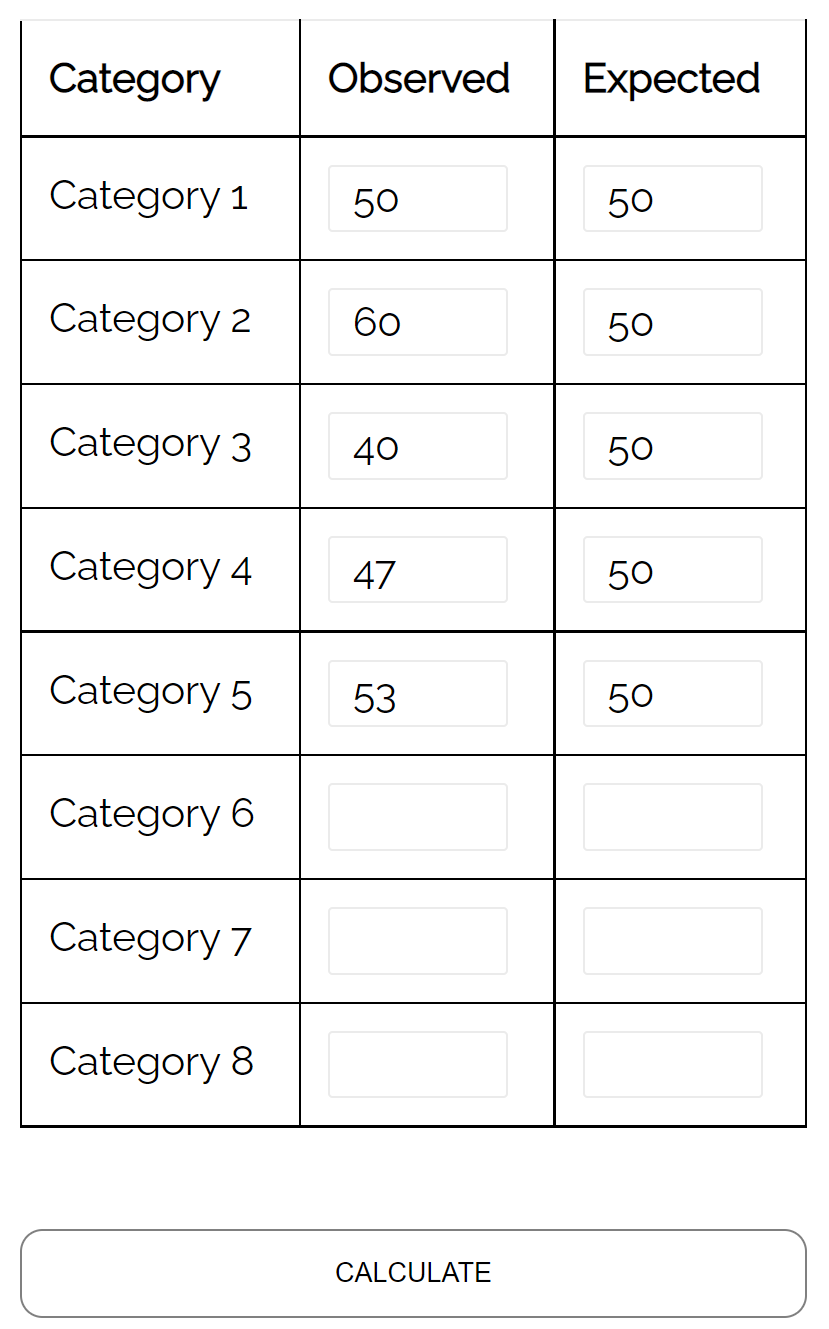
假设一家商店老板声称一周中每天都有相同数量的顾客来到他的商店。
为了检验这个假设，他记录了给定一周内进入商店的顾客数量，并发现以下结果：
- 周一： 50 位顾客
- 周二： 60 位顾客
- 周三： 40 位顾客
- 周四： 47 位顾客
- 周五： 53 位顾客
他可以使用卡方拟合优度检验来确定每天来的顾客的分布是否与他的分布假设一致。
使用卡方拟合优度检验计算器，他可以看到检验的 p 值为0.359 。
由于该 p 值不小于 0.05，因此没有足够的证据表明顾客的真实分布与店主声称的不同。
示例 2：卡方拟合优度检验
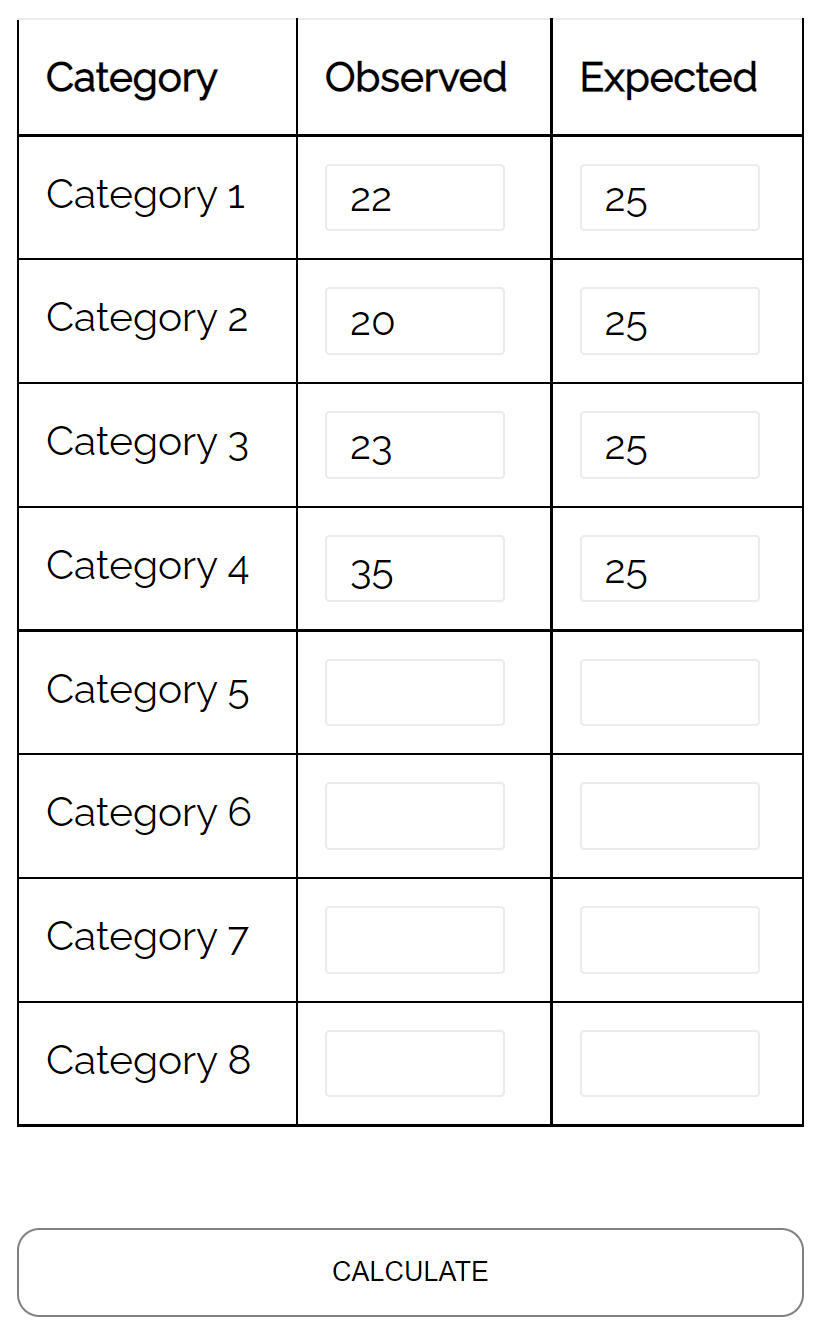
假设一位生物学家声称每周有相同数量的四种不同种类的鹿进入森林的某个林区。
为了检验这个假设，她记录了一周内进入树林地区的每种鹿的数量：
- 物种#1： 22
- 物种#2： 20
- 物种#3： 23
- 物种#4： 35
她可以使用卡方拟合优度检验来确定每周进入森林林区的鹿物种分布是否与其假设分布一致。
使用卡方拟合优度检验计算器，她可以看到检验的 p 值为0.137 。
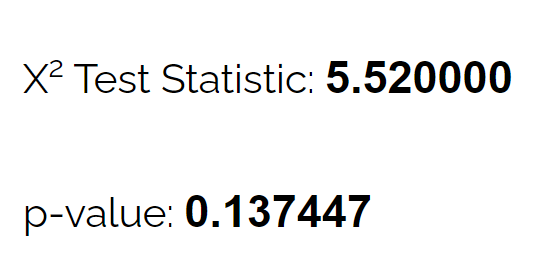
由于该 p 值不小于 0.05，因此没有足够的证据表明鹿的真实分布与生物学家声称的不同。
示例 3：卡方独立性检验
假设某个城市的政策制定者想知道性别是否与政党偏好相关。
他决定对 500 名选民进行简单随机抽样，并询问他们的政党偏好。下表列出了调查结果：
| 共和党人 | 民主党人 | 独立的 | 全部的 | |
| 男性 | 120 | 90 | 40 | 250 |
| 女性 | 110 | 95 | 45 | 250 |
| 全部的 | 230 | 185 | 85 | 500 |
它可以使用卡方独立性检验来确定两个变量之间是否存在统计上显着的关联。
使用 卡方独立性检验计算器，他可以看到检验的 p 值为0.649 。
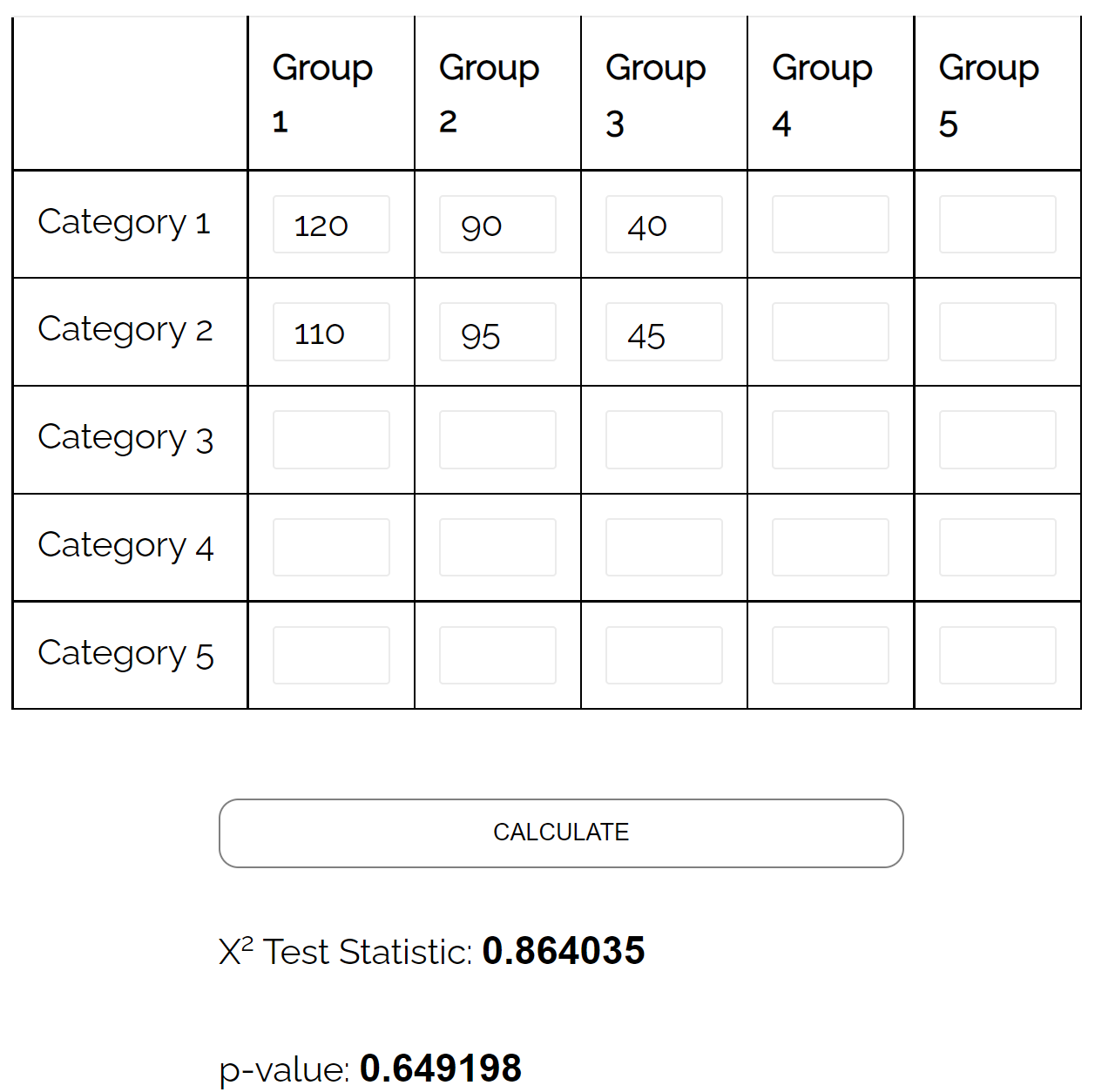
由于 p 值不小于 0.05，因此没有足够的证据表明性别和政党偏好之间存在关联。
示例 4：卡方独立性检验
假设研究人员想知道婚姻状况是否与教育程度相关。
他决定对 300 人进行简单随机抽样，得到以下结果：
| 中学 | 学士 | 硕士或以上 | 全部的 | |
| 已婚 | 20 | 100 | 35 | 155 |
| 学士 | 50 | 80 | 15 | 145 |
| 全部的 | 70 | 180 | 50 | 300 |
它可以使用卡方独立性检验来确定两个变量之间是否存在统计上显着的关联。
使用 卡方独立性检验计算器，他可以看到检验的 p 值为0.000011 。
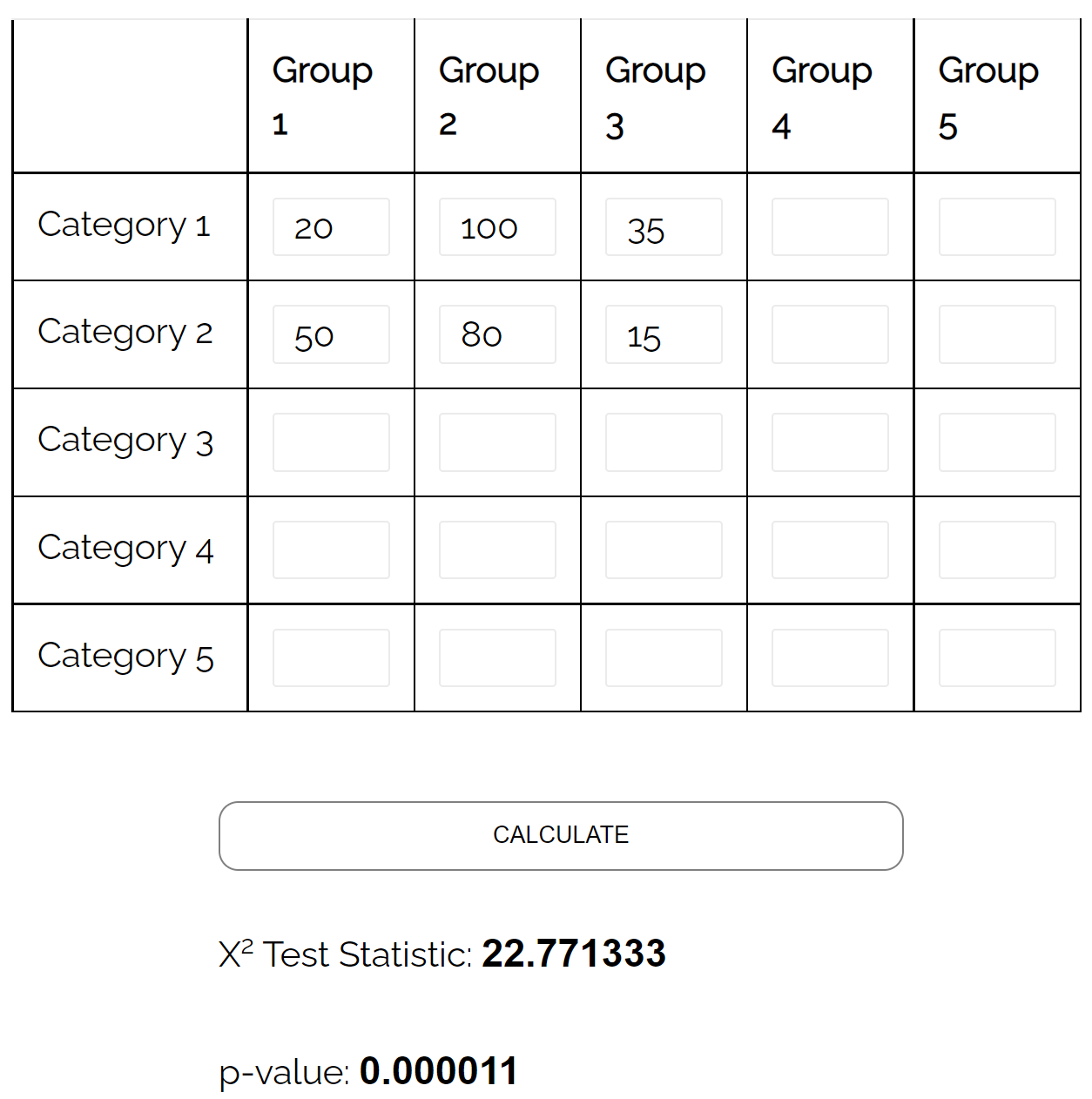
由于 p 值小于 0.05，因此有足够的证据表明婚姻状况和教育水平之间存在关联。
其他资源
以下教程介绍了不同类型的卡方检验：
以下教程解释了卡方检验和其他统计检验之间的区别：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多