什么被视为原始数据？ （定义和示例）

在统计学中，原始数据是指直接从主要来源收集且未经任何处理的数据。

在任何类型的数据分析项目中，第一步都是收集原始数据。一旦收集到这些数据，就可以对其进行清理、转换、总结和可视化。

收集原始数据的优点是最终能够使用它来更好地理解某些现象或使用它来构建一种预测模型。

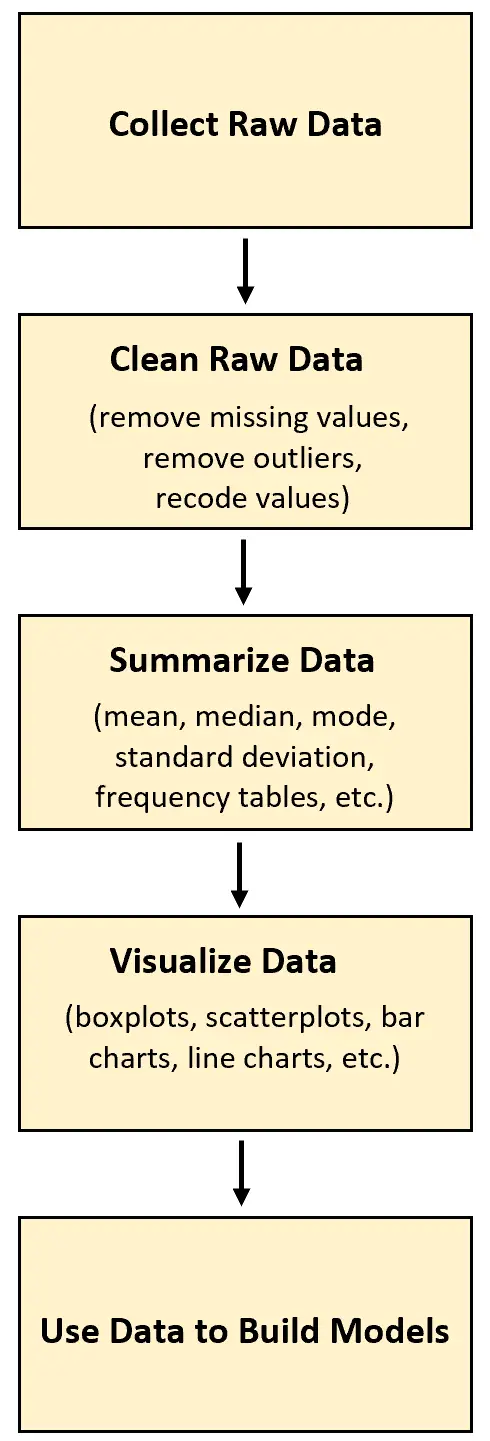
以下示例说明了如何在现实生活中收集和使用原始数据。

示例：原始数据的收集和使用

体育是经常收集原始数据的领域。例如，可以收集有关职业篮球运动员的各种统计的原始数据。

第 1 步：收集原始数据

想象一下，一名篮球球探收集了职业篮球队 10 名球员的以下原始数据：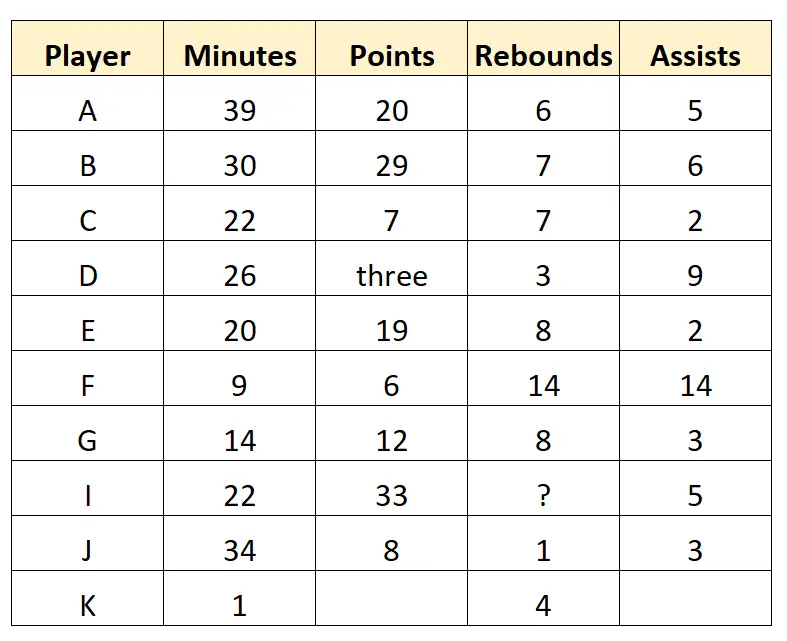

该数据集代表原始数据，因为它是由侦察员直接收集的，并且没有以任何方式进行清理或处理。

第2步：清理原始数据

在使用这些数据创建汇总表、图表或其他任何内容之前，侦察员必须首先删除任何缺失值并清理任何“脏”数据值。

例如，我们可能会在数据集中发现几个需要转换或删除的值：

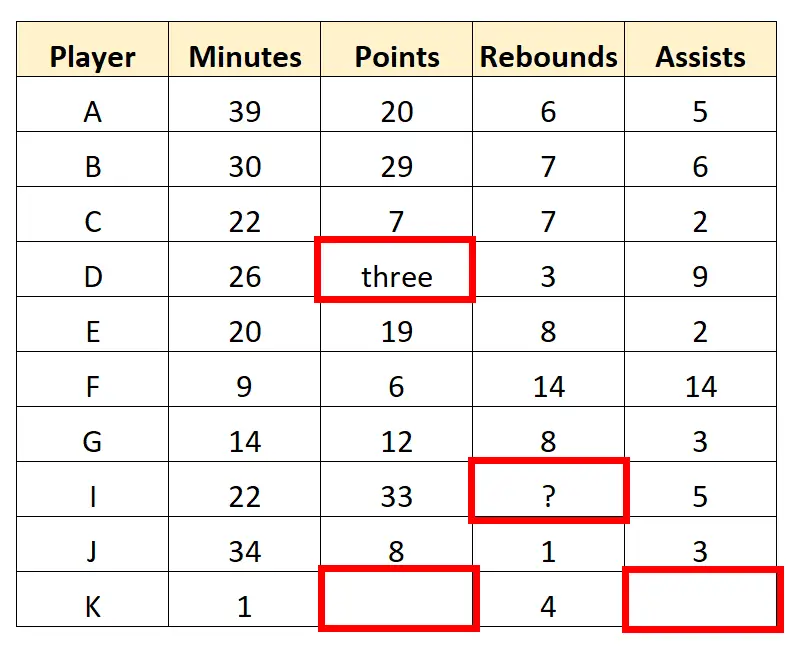
侦察员可能决定完全删除最后一行，因为它有几个缺失值。然后它可以清理数据集中的字符值以获得以下“干净”的数据：

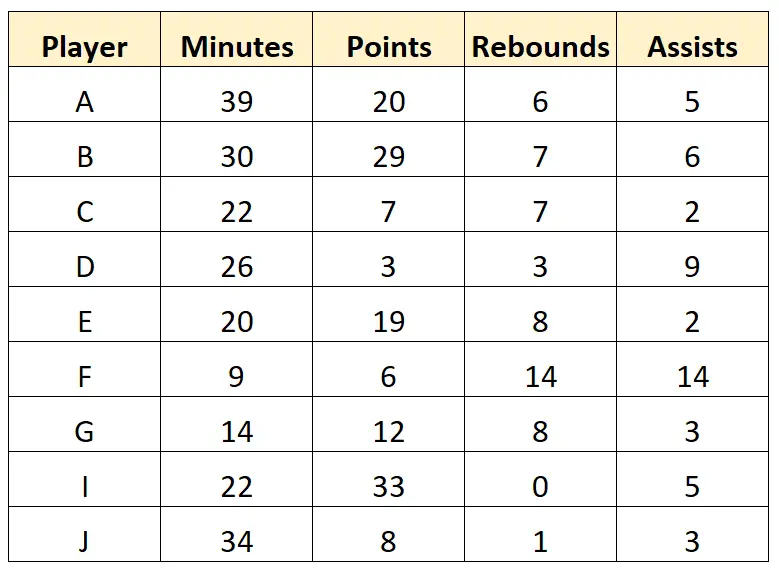
第三步：总结数据

一旦数据被清理，侦察员就可以总结数据集中的每个变量。例如，它可以计算“分钟”变量的以下汇总统计数据：

• 平均：24 分钟
• 中位时间：22 分钟
• 标准偏差：9.45 分钟

第 4 步：可视化数据

然后，侦察员可以可视化数据集中的变量，以更好地理解数据值。

例如，他可以创建以下条形图来可视化每个球员的总上场时间：

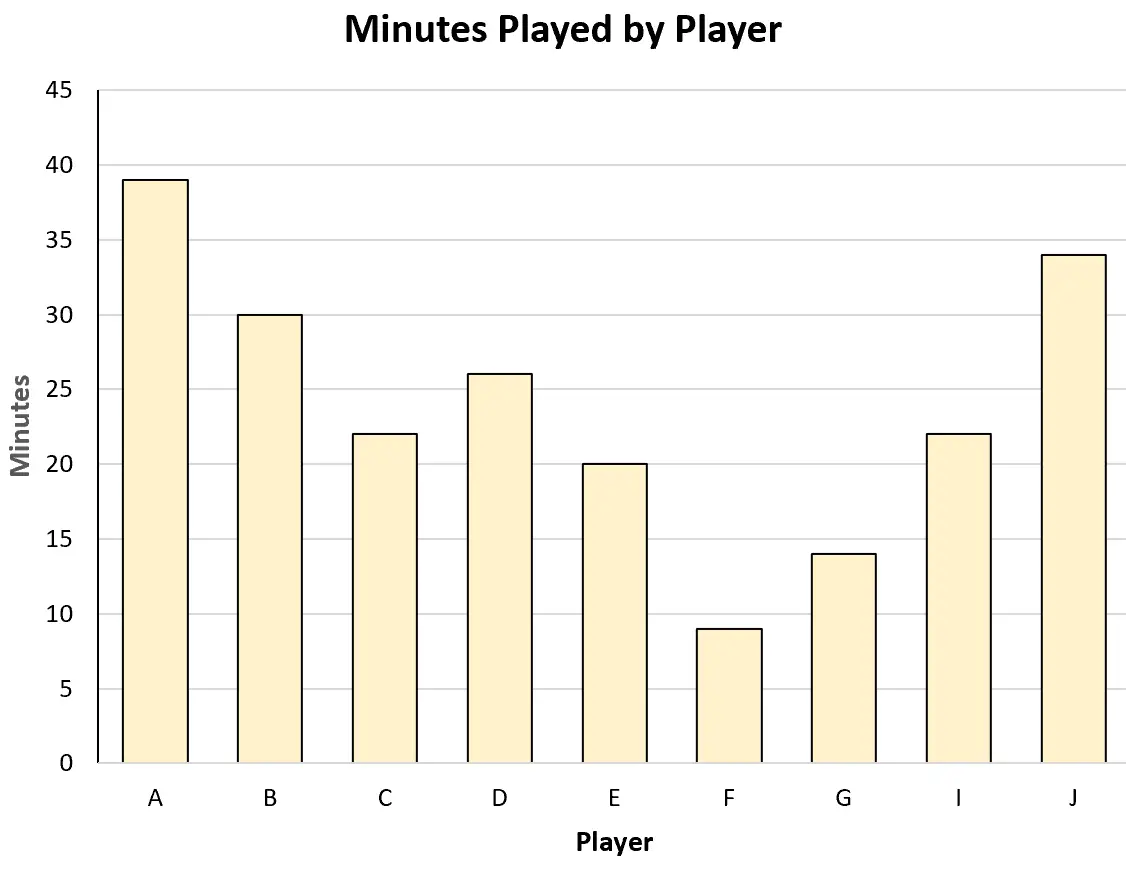
或者他可以创建以下散点图来可视化上场时间和得分之间的关系：

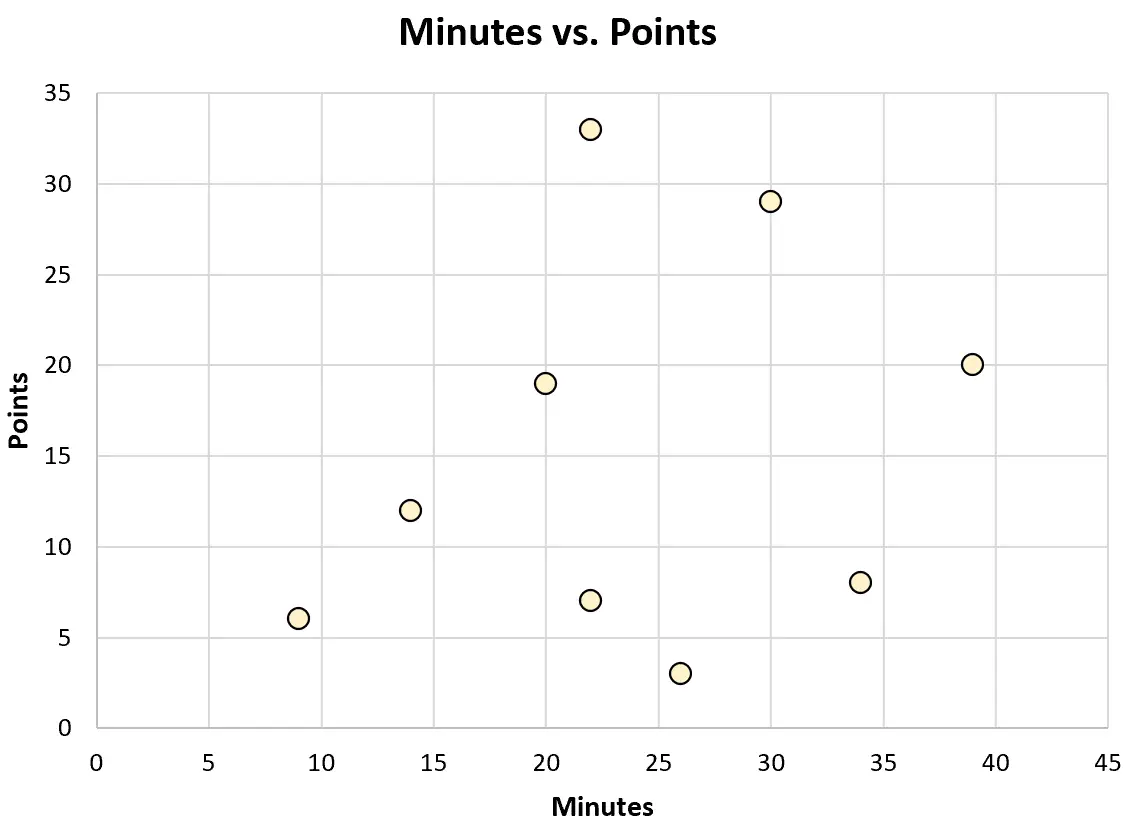
每种类型的图表都可以帮助他更好地理解数据。

第 5 步：使用数据构建模型

最后，一旦数据被清理，侦察员就可以决定采用某种类型的预测模型。

例如，它可以拟合一个简单的线性回归模型，并使用比赛时间来预测每个球员的总得分。

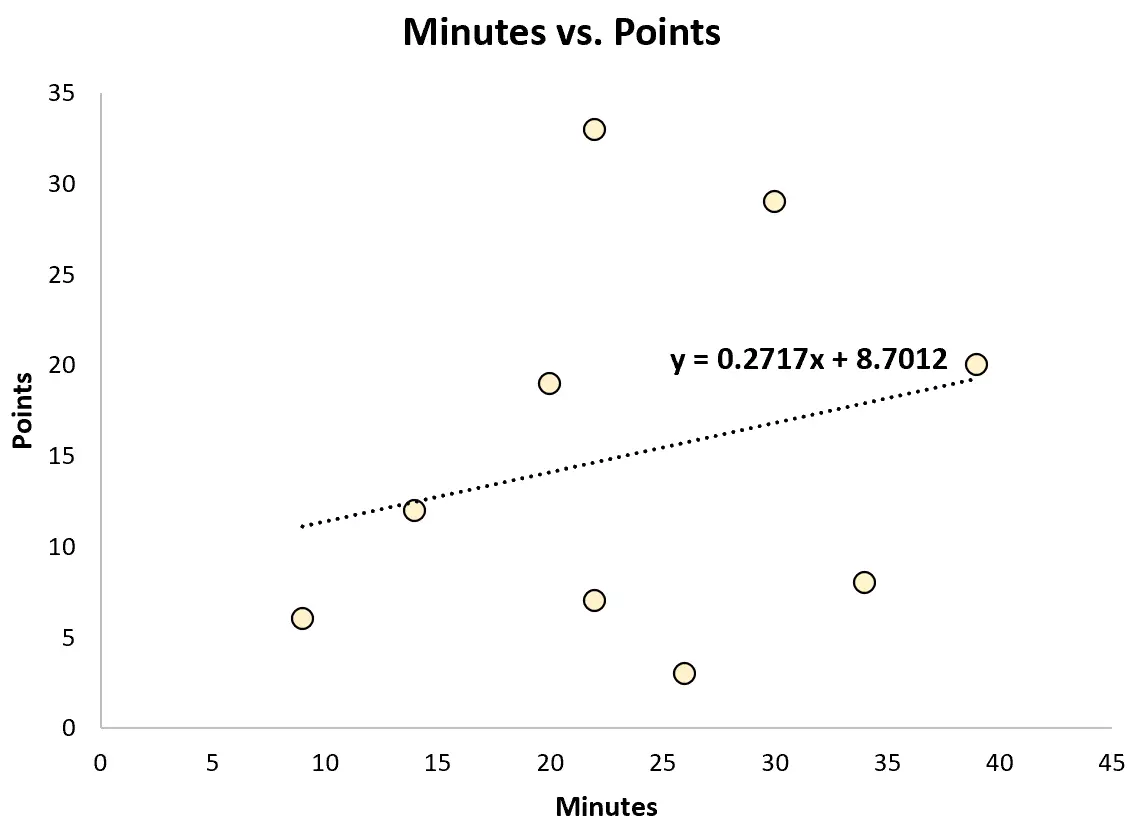
拟合的回归方程为：

积分 = 8.7012 + 0.2717*（分钟）

然后球探可以使用这个方程来预测球员根据上场时间的得分。例如，一名比赛 30 分钟的运动员应得分16.85分：

积分 = 8.7012 + 0.2717*(30) = 16.85

其他资源

为什么统计数据很重要？
为什么样本量在统计学中很重要？
统计学中的观察是什么？
统计学中的表格数据是什么？