如何用 python 计算库克距离

库克距离用于识别回归模型中有影响的观测值。

库克距离的公式为：

d _i = (r _i ² / p*MSE) * (h _ii / (1-h _ii ) ² )

金子：

• r _i是第 i^个残基
• p是回归模型中的系数数量
• MSE是均方误差
• h _ii为^{第 i}个杠杆值

本质上，库克距离衡量的是当第 i^个观测值被移除时模型的所有拟合值发生了多少变化。

库克距离的值越大，给定观测的影响力就越大。

作为一般规则，库克距离大于 4/n（其中n = 总观测值）的任何观测值都被认为具有较大影响。

本教程提供了如何在 Python 中计算给定回归模型的库克距离的分步示例。

第 1 步：输入数据

首先，我们将创建一个在 Python 中使用的小数据集：

 import pandas as pd

#create dataset
df = pd. DataFrame ({' x ': [8, 12, 12, 13, 14, 16, 17, 22, 24, 26, 29, 30],
                   ' y ': [41, 42, 39, 37, 35, 39, 45, 46, 39, 49, 55, 57]})

步骤 2：拟合回归模型

接下来，我们将拟合一个简单的线性回归模型：

 import statsmodels. api as sm

#define response variable
y = df[' y ']

#define explanatory variable
x = df[' x ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

第 3 步：计算烹饪距离

接下来，我们将计算模型中每个观测值的库克距离：

 #suppress scientific notation
import numpy as np
n.p. set_printoptions (suppress= True )

#create instance of influence
influence = model. get_influence ()

#obtain Cook's distance for each observation
cooks = influence. cooks_distance

#display Cook's distances
print (cooks)

(array([0.368, 0.061, 0.001, 0.028, 0.105, 0.022, 0.017, 0. , 0.343,
        0. , 0.15 , 0.349]),
 array([0.701, 0.941, 0.999, 0.973, 0.901, 0.979, 0.983, 1. , 0.718,
        1. , 0.863, 0.713]))

默认情况下， cooks_distance()函数显示每个观测值的 Cook 距离值数组，后跟相应的 p 值数组。

例如：

• 观察 #1 的库克距离： 0.368 （p 值：0.701）
• 观察 #2 的库克距离： 0.061 （p 值：0.941）
• 观察 #3 的库克距离： 0.001 （p 值：0.999）

等等。

第四步：可视化厨师的距离

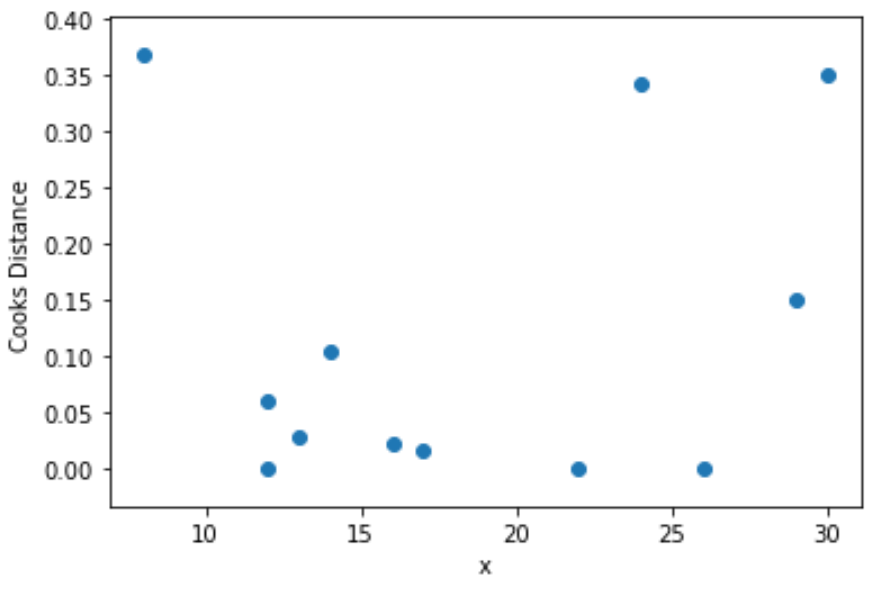
最后，我们可以创建一个散点图，将预测变量的值可视化为每次观测的库克距离的函数：

 import matplotlib. pyplot as plt

plt. scatter (df.x, cooks[0])
plt. xlabel (' x ')
plt. ylabel (' Cooks Distance ')
plt. show () 

最后的想法

值得注意的是，库克距离应用于识别潜在影响的观测结果。仅仅因为观察有影响并不意味着它应该从数据集中删除。

首先，您需要验证观察结果不是数据输入错误或其他奇怪事件的结果。如果结果证明它是合法值，您可以决定是否适当将其删除、保留原样，或者简单地将其替换为中位数等替代值。