了解回归斜率的标准误差

经过本杰明·安德森博 7月 23, 2023 指导 0 条评论

回归斜率的标准误差是衡量回归斜率估计“不确定性”的一种方法。

计算方法如下：

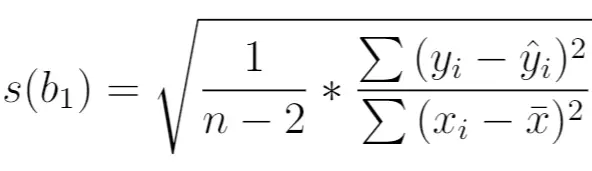
回归斜率标准误差公式

金子：

标准误差越小，回归斜率系数估计值的变异性就越低。

大多数统计软件的回归输出中，回归斜率的标准误差将显示在“标准误差”列中：

以下示例展示了如何解释两种不同情况下回归斜率的标准误差。

假设一位教授想要了解他班上学生的学习时数和期末考试成绩之间的关系。

它收集 25 名学生的数据并创建以下散点图：

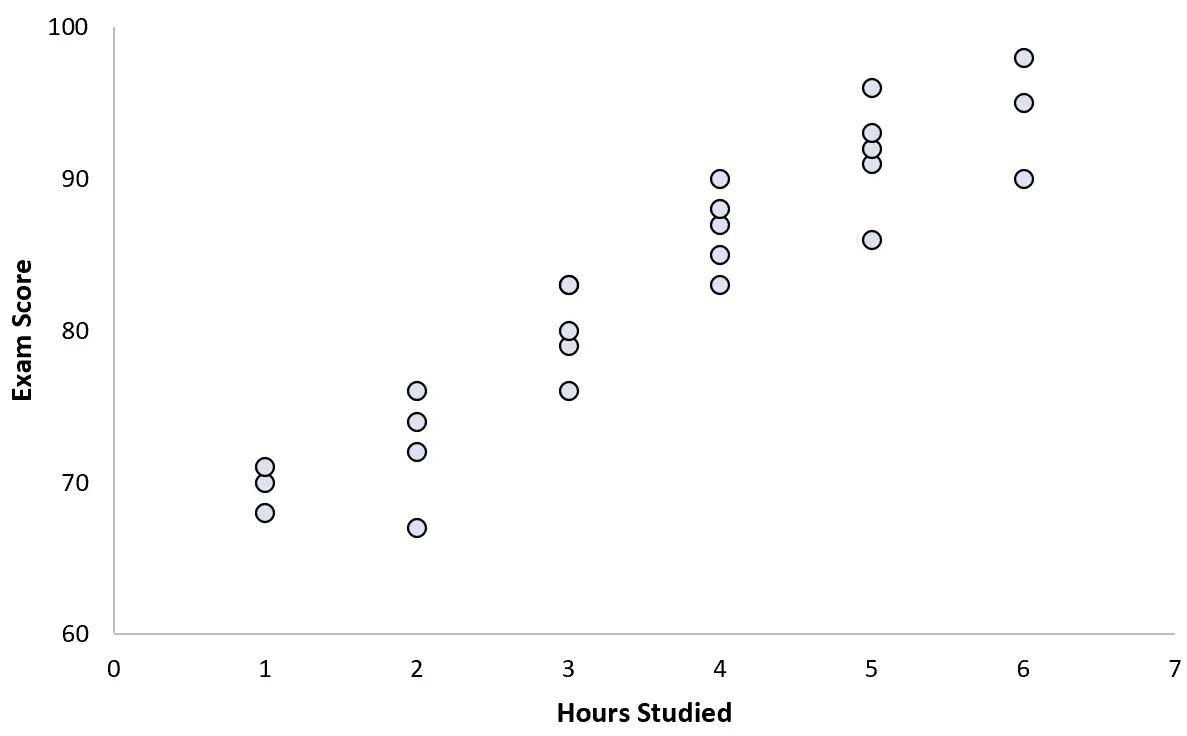
这两个变量之间存在明显的正相关关系。随着学习时间的增加，考试成绩以相当可预测的速度增加。

然后，他使用学习时间作为预测变量、期末考试成绩作为响应变量来拟合一个简单的线性回归模型。

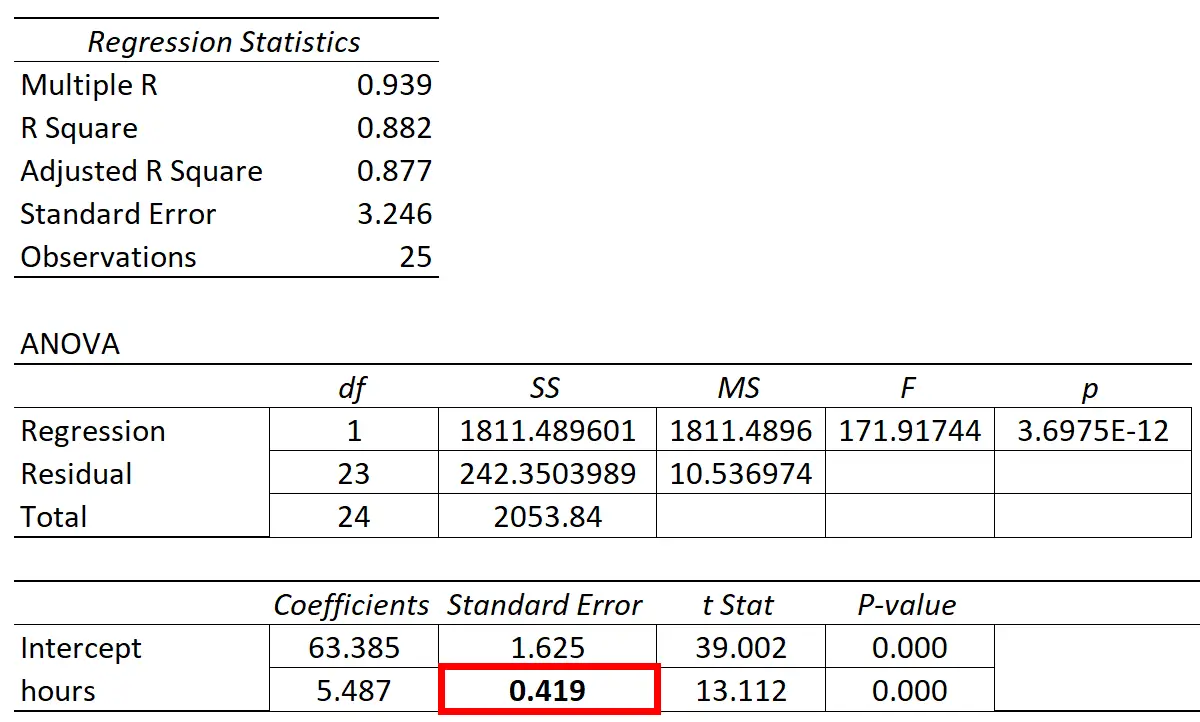
下表显示了回归结果：

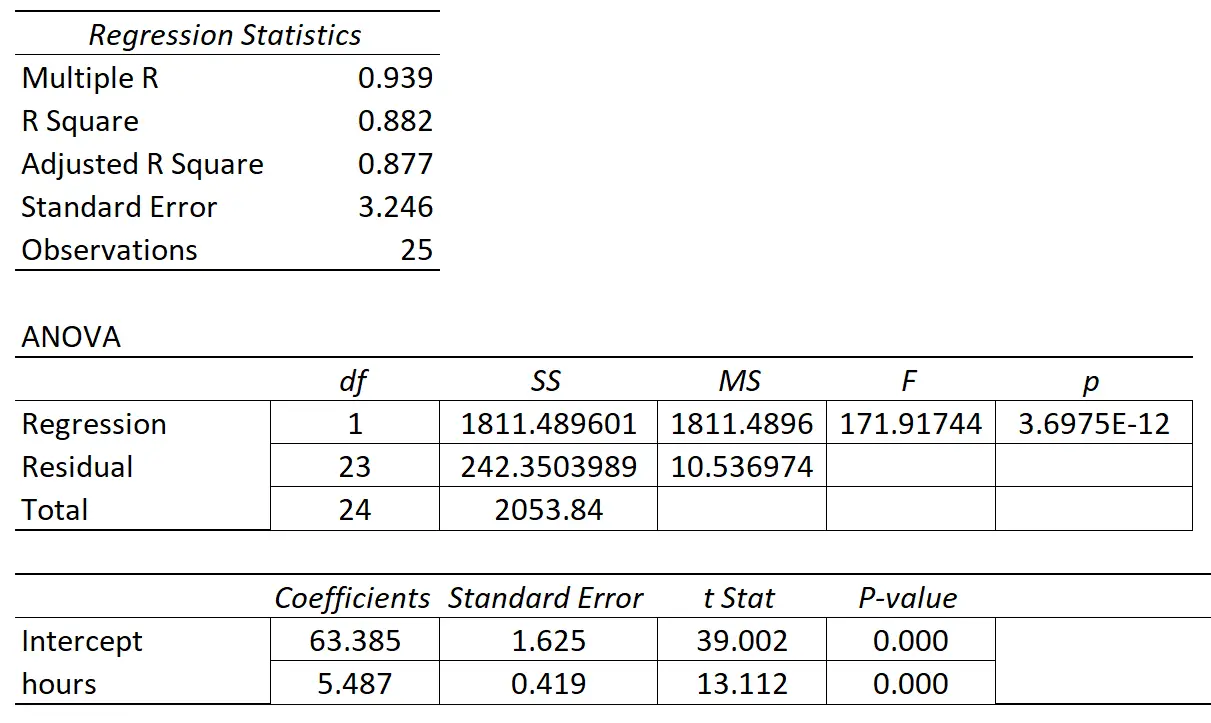
预测变量“学习时间”的系数为 5.487。这告诉我们，每多学习一小时，考试成绩就会平均增加5,487分。

标准误差为0.419 ，表示回归斜率估计值周围变异性的度量。

我们可以使用该值来计算预测变量“学习时间”的 t 统计量：

与此检验统计量对应的 p 值为 0.000，这表明“学习时间”与期末考试成绩具有统计显着关系。

由于与回归斜率的系数估计相比，回归斜率的标准误差较小，因此预测变量具有统计显着性。

假设另一位教授想要了解他班上学生的学习小时数和期末考试成绩之间的关系。

她收集了 25 名学生的数据并创建了以下散点图：

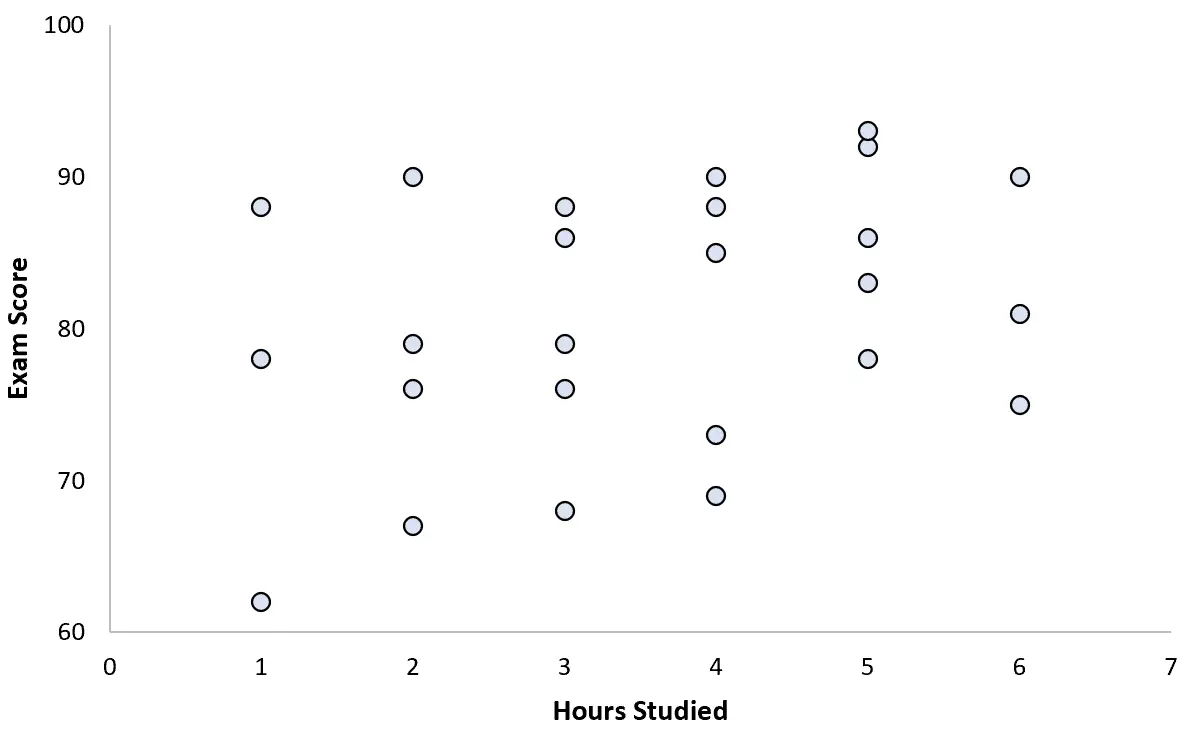
这两个变量之间似乎存在轻微的正相关关系。随着学习时间的增加，考试成绩通常会增加，但速度不会以可预测的速度增加。

假设教授随后使用学习时间作为预测变量、期末考试成绩作为响应变量来拟合一个简单的线性回归模型。

下表显示了回归结果：

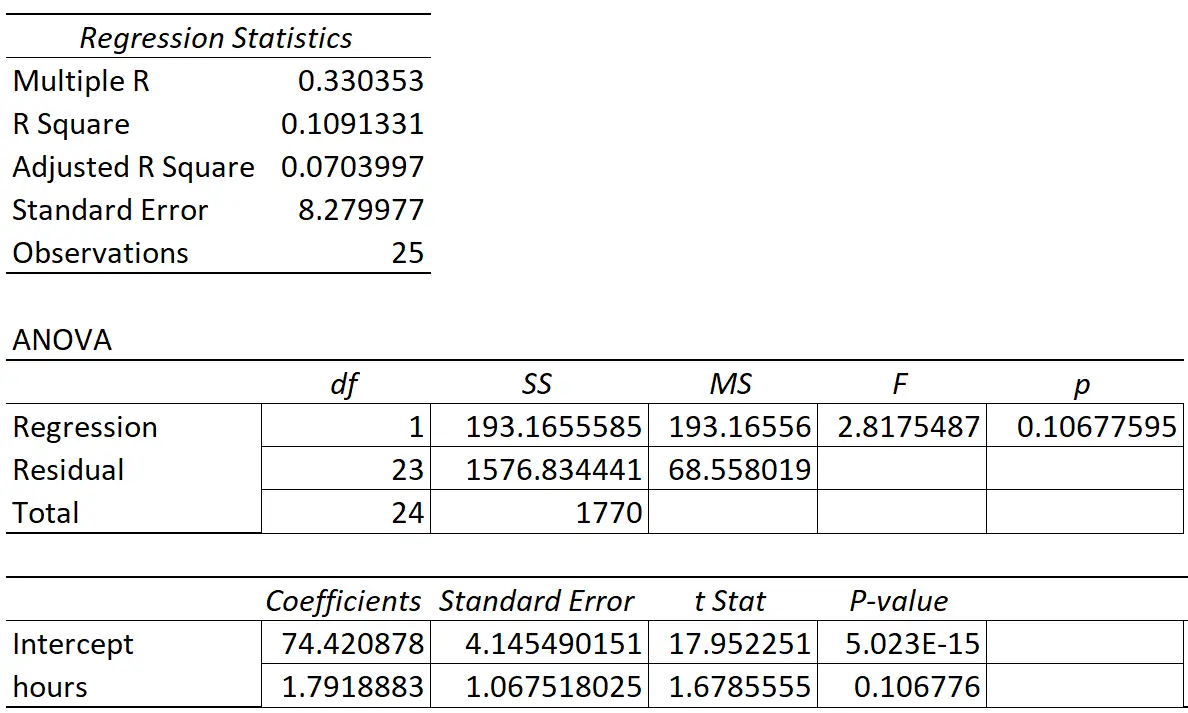
预测变量“学习时间”的系数为 1.7919。这告诉我们，每多学习一小时，考试成绩就会平均提高1.7919 。

标准误差为1.0675 ，它是回归斜率估计值周围变异性的度量。

我们可以使用该值来计算预测变量“学习时间”的 t 统计量：

与此检验统计量对应的 p 值为 0.107。由于该 p 值不小于 0.05，这表明“学习时间”与期末考试成绩没有统计显着关系。

由于回归斜率的标准误差相对于回归斜率的系数估计值较大，因此预测变量不具有统计显着性。

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多