回归线
本文解释了统计学中的回归线。因此,您将了解如何计算两个变量之间的回归线、已解决的练习以及用于计算任何数据样本的回归线的在线计算器。
什么是回归线?
在统计学中,回归线是从简单线性回归模型得到的线。更准确地说,回归线是最适合散点图的线,因此最能描述一组统计数据。
因此,回归线方程在数学上将一组数据的自变量 X 和因变量 Y 联系起来。尽管回归线通常无法精确确定每个观测值,但它可以提供其值的近似值。

正如您在上图中所看到的,回归线帮助我们了解数据集的趋势以及自变量和因变量之间存在什么类型的关系。下面我们来看看回归线的应用。
回归线公式
现在我们知道了回归线的定义,让我们看看如何计算线性回归模型的直线方程。
与任何直线一样,回归线的方程由常数 (b 0 ) 和斜率 (b 1 ) 组成:
![]()
因此,线性回归线系数的计算公式如下:
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6dc6f56cacf0a233977c358d6a62fca8_l3.png)
金子:
-
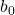
是回归线的常数。
-
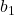
是回归线的斜率。
-

是数据 i 的自变量 X 的值。
-

是数据 i 的因变量 Y 的值。
-

是自变量值的平均值
-

是因变量 Y 值的平均值。
👉您可以使用下面的计算器来计算任何数据集的回归线。
回归线的具体示例
为了进一步探讨回归线的概念,下面是如何创建回归线的工作示例。
- 在参加统计考试后,五名学生被问及他们在考试上花费了多少时间,数据如下表所示。根据收集的统计数据计算回归线,将学习时间与获得的成绩线性相关。接下来,确定学习 8 小时的学生将获得什么成绩。

为了找到样本数据的回归线,我们需要确定方程的系数 b 0和 b 1 ,为此,我们需要使用上一节中看到的公式。
然而,要应用线性回归线的公式,我们必须首先计算自变量的平均值和因变量的平均值:
![Rendered by QuickLaTeX.com \begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7a7aa6f1f20fa4ff0d61a2ad0dd2ea1f_l3.png)
现在我们知道了变量的均值,我们使用相应的公式计算模型的系数 b 1 :
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c9d90c766487cd7b6924e6b23d2d9c78_l3.png)
最后,我们使用相应的公式计算模型的系数b 0 :
![Rendered by QuickLaTeX.com \begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c72e6b89a75681a88cf751ca39079240_l3.png)
简而言之,问题的线性回归线方程如下:
![]()
下面您可以看到样本数据的图形表示以及简单线性回归模型的直线:

一旦我们计算出回归线,要预测学习 8 小时的学生将获得的成绩,只需将该值代入所获得的回归线方程即可:
![]()
因此,根据所进行的线性回归模型,如果一个学生学习了八个小时,他的考试成绩将为5.56。
回归线有什么用?
回归线主要有两个用途:回归线用于确定两个变量之间存在什么类型的关系,另一方面,回归线还允许您对新观察值进行预测。
回归线的斜率告诉我们自变量和因变量之间的相关性如何。如果斜率为正,则表示因变量与自变量成正比;如果斜率为负,则表示变量与自变量成反比。最后,如果斜率系数非常接近于零,这意味着两个变量之间的相关性非常弱。
此外,如果回归线的方程已知,则可以根据自变量的新值来预测因变量的值,就像我们在上面的示例中所做的那样。因此,回归线适应得越好,它做出的预测就越好。
回归线计算器
在以下计算器中输入数据样本以计算两个变量之间的回归线。您需要分离数据对,以便第一个框中只有自变量 X 的值,第二个框中只有因变量 Y 的值。
数据必须用空格分隔,并使用句点作为小数点分隔符输入。