因变量和自变量

本文解释了什么是因变量和自变量。因此，您将了解因变量和自变量之间的区别，如何知道哪个是因变量，哪个是自变量，此外，还提供了此类变量的几个示例。

什么是因变量和自变量？

因变量是其值取决于另一个变量（即自变量）的变量。因此，因变量和自变量之间的区别在于，自变量不依赖于任何其他变量，但因变量取决于自变量的值。

在图表中，自变量由横坐标（水平轴）上的字母x表示，而因变量由纵坐标（垂直轴）上的字母y表示。

例如，如果在统计研究中我们分析所获得的成绩与投入的学习时间之间的关系，则投入的学习时间是自变量，所获得的成绩是因变量。因为获得的成绩取决于学习的时间，而不是相反。

因变量和自变量的示例

在上一节中我们看到了因变量和自变量的定义，所以现在我们将看到此类变量的十个示例，以更好地理解其含义。

1. 学习时间（自变量）影响获得的成绩（因变量）。
2. 产品的价格（自变量）会改变愿意购买该产品的人数（因变量）。
3. 一个人的健康（因变量）取决于他们的饮食（自变量）。
4. 一个人的心率（因变量）受到其心率（自变量）的影响。
5. 环境温度（自变量）影响森林火灾的数量（因变量）。
6. 客户满意度水平（因变量）根据所提供服务的质量（自变量）而变化。
7. 产品广告（自变量）会影响该产品的销售数量（因变量）。
8. 一个国家排放的污染物质的数量（因变量）取决于该国的工业生产（自变量）。
9. 出租车司机的工资（因变量）根据他的出行次数（自变量）而变化。
10. 城市的居民数量（自变量）与城市的出租车数量（因变量）相关。

请记住，变量是依赖的还是独立的取决于上下文，因为根据调查，它将充当关系的原因或结果。

因变量和自变量练习

下列情况中，哪个是因变量，哪个是自变量？

1. 城市居民数量 – 公共巴士数量
2. 车龄 – 车辆状况
3. 蚊子数量 – 环境温度
4. 每月下雨天数——雨伞需求

1. 因变量：公共巴士数量 – 自变量：城市居民数量
2. 因变量：车辆状况 – 自变量：车龄
3. 因变量：蚊子数量 – 自变量：环境温度
4. 因变量：雨伞需求 – 自变量：每月下雨天数

数学中的因变量和自变量

在数学中，因果关系通常使用自变量和因变量来建模。因此，函数定义了因变量和自变量之间存在的数学关系。

因变量通常用字母y表示，另一方面，字母x通常用于表示自变量。

例如，函数y=2x表示当自变量x增加1个单位时，因变量y增加两倍。

要了解有关数学函数的更多信息，您可以访问我们的合作伙伴网站function.xyz 。

统计中的因变量和自变量

然而，实际上，很难找到可以通过精确的数学函数定义的两个变量之间的关系，因为有时自变量的相同值会导致因变量的不同值。

例如，有时，通过学习更多，我们会得到较低的成绩，或者相反，通过学习较少，我们会得到更好的成绩。因此，我们投入学习的时间并不是影响成绩的唯一因素，它还会根据考试的难度或所学习材料的难度而变化。

因此，在统计学中，通常会进行许多实验来确定两个变量之间是否存在关系，其中一个是自变量，另一个是因变量。然后，可以以图形方式表示获得的结果，以检查变量是否相关，如果是，则查看它们具有什么类型的关系（正、负、线性、指数等）。

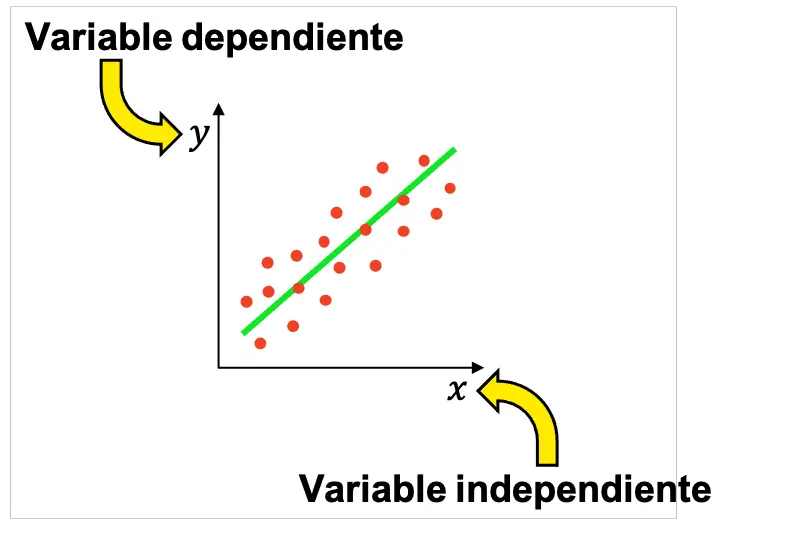
请记住，尽管最基本的统计研究是使用一个自变量和一个因变量进行的，但在一项调查中可能有多个自变量。

一旦进行了统计研究，就可以计算数学函数来进行近似，从而对变量之间的关系进行建模。所以通常先建立统计模型，然后再建立数学模型。