因果关系是否意味着相关性？ （3个例子）

众所周知， 相关性并不意味着因果关系。

举个简单的例子，如果我们每年收集美国高中毕业生总数和披萨总消费量的数据，我们会发现这两个变量是高度相关的：

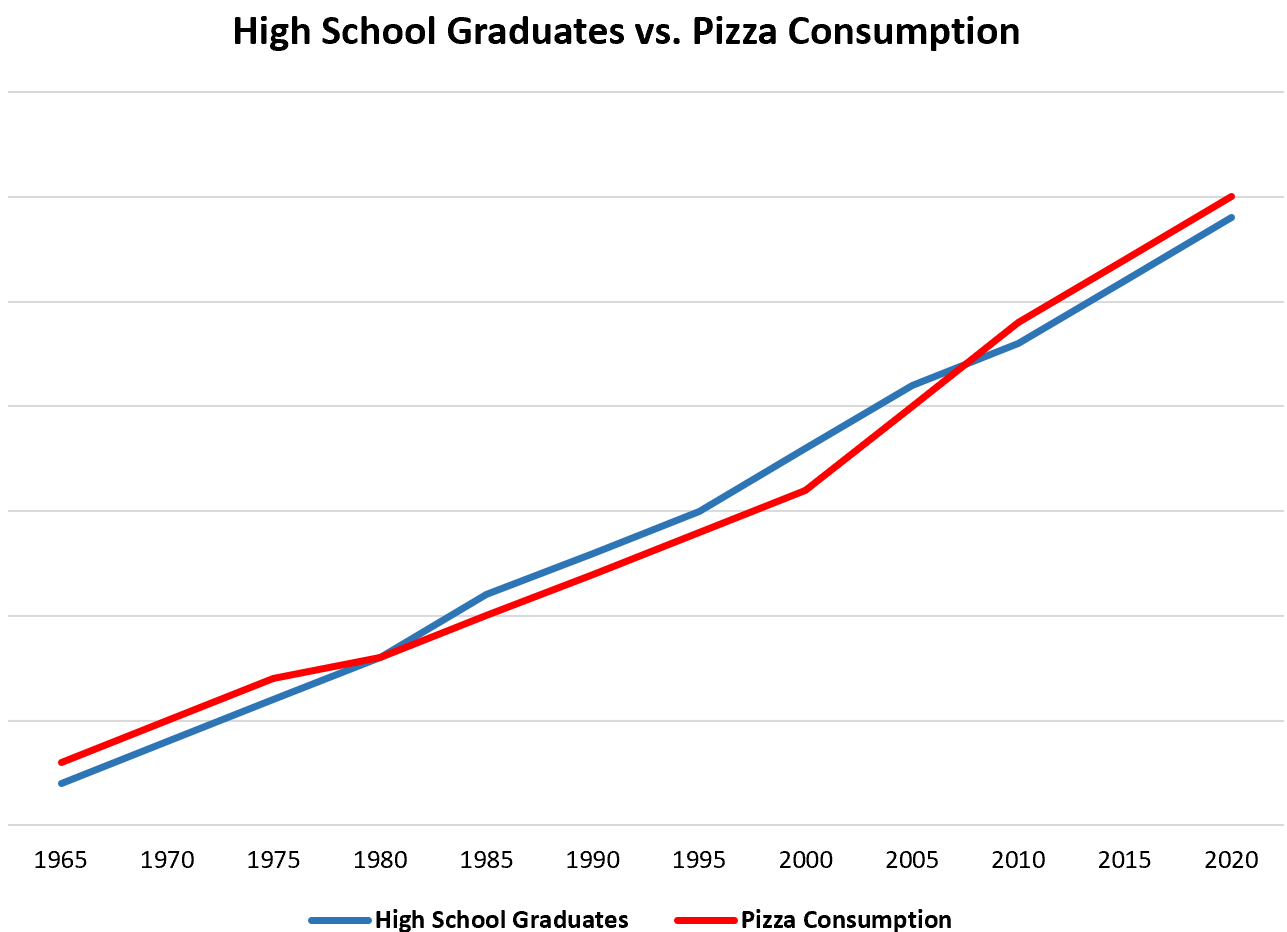
这并不意味着高中毕业生人数的增加导致披萨消费量的增加。

最可能的解释是，美国人口随着时间的推移而增加，这意味着拥有高中文凭的人数和消费的披萨总量随着人口的增加而增加。

但相反的说法又如何：因果关系是否意味着相关性？

如果一个变量引起另一个变量，是否一定意味着这两个变量将相关？

简短的回答：不。

以下示例说明了原因。

示例 1：二次关系

假设变量 X 导致变量 Y 的值等于 X ² 。

例如：

• 如果 X = -10 则 Y = -10 ² = 100
• 如果 X = 0 则 Y = 0 ² = 0
• 如果 X = 10 则 Y = 10 ² = 100

等等。

如果我们绘制 X 和 Y 之间的关系，它将如下所示：

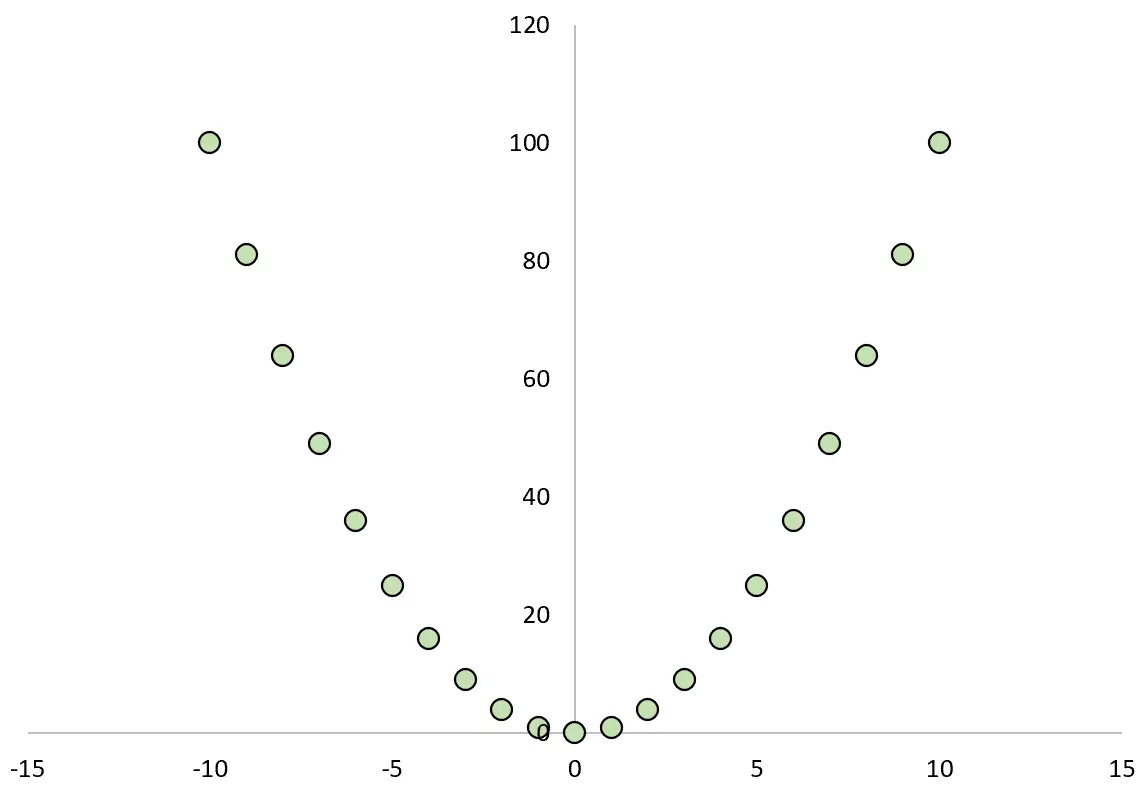
如果我们计算两个变量之间的皮尔逊相关系数，我们会发现相关性为零。

虽然 X 导致 Y，但两个变量之间的线性相关性为零。

示例2：四次关系

假设变量 X 导致变量 Y 的值等于 X ⁴ 。

例如：

• 如果 X = -10 则 Y = -10 ⁴ = 10,000
• 如果 X = 0 则 Y = 0 ⁴ = 0
• 如果 X = 10 则 Y = 10 ⁴ = 10,000

等等。

如果我们绘制 X 和 Y 之间的关系，它将如下所示：

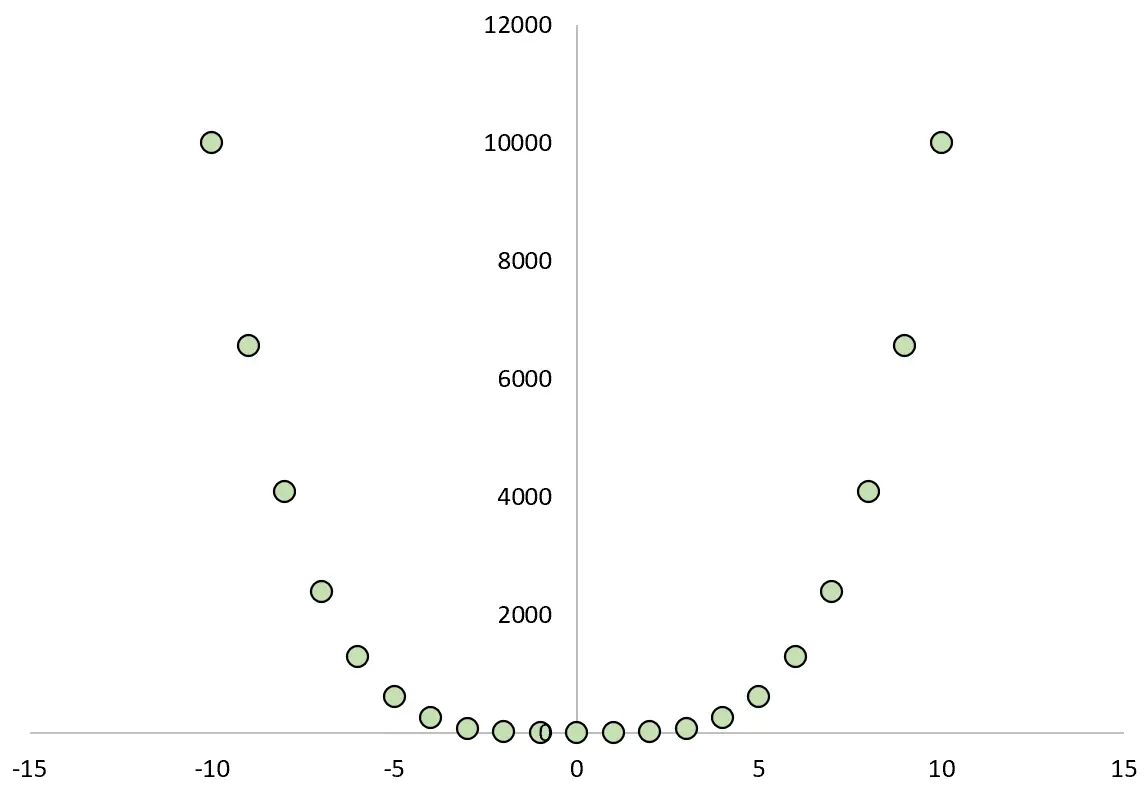
如果我们计算两个变量之间的皮尔逊相关系数，我们会发现相关性为零。

我们知道 X 导致 Y，但是两个变量之间的线性相关性为零。

示例3：余弦关系

假设变量 X 导致变量 Y 的值等于 cos(X)。

例如：

• 如果 X = -10 则 Y = cos(-10) = -0.83907
• 如果 X = 0，则 Y = cos(0) = 1
• 如果 X = 10，则 Y = cos(10) = -0.83907

等等。

如果我们绘制 X 和 Y 之间的关系，它将如下所示：

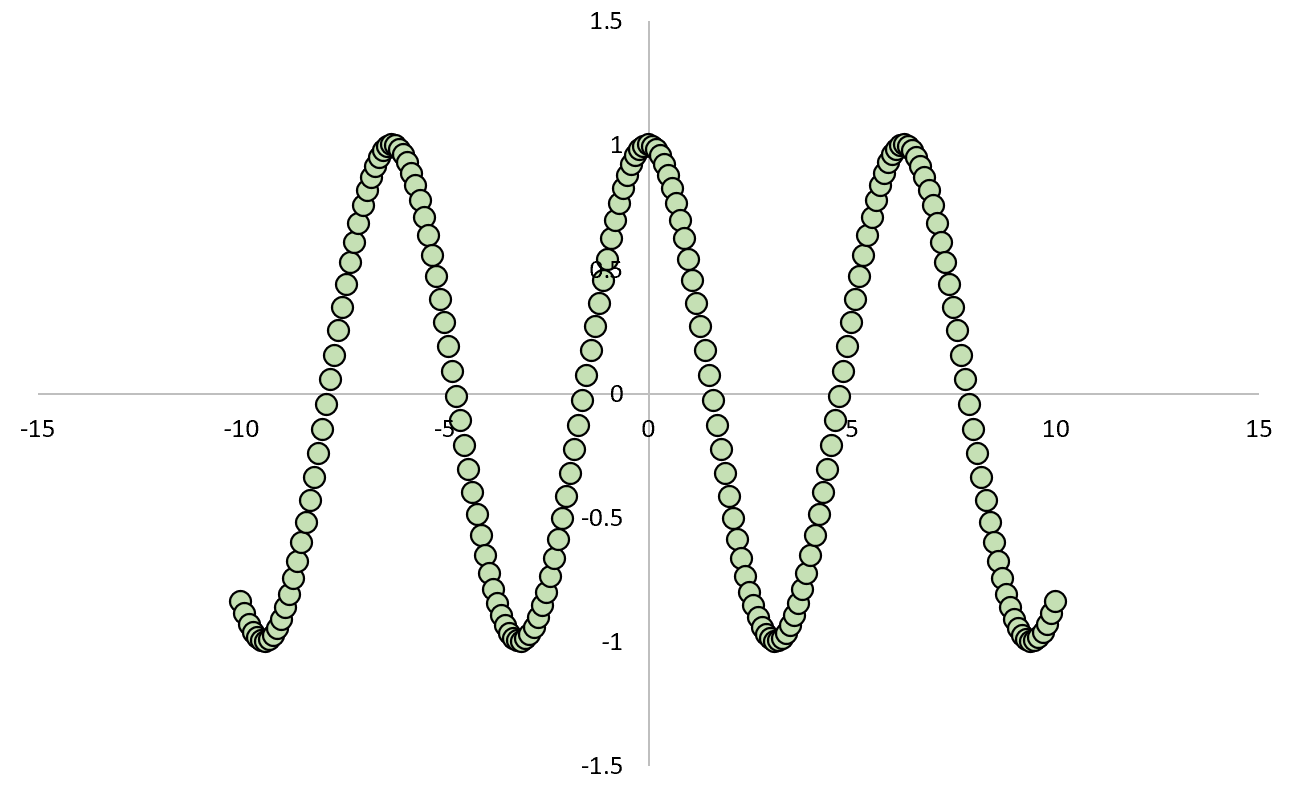
如果我们计算两个变量之间的皮尔逊相关系数，我们会发现相关性为零。

我们知道 X 导致 Y，但是两个变量之间的线性相关性为零。

其他资源

以下教程提供有关相关性和因果关系的其他信息：

相关性并不意味着因果关系：5 个具体例子
皮尔逊相关系数简介
反向因果关系：定义和示例