图基 vs.邦费罗尼 vs 邦费罗尼scheffe:您应该使用哪种测试?
单向方差分析用于确定三个或更多独立组的平均值之间是否存在统计显着差异。
如果方差分析表的总体p 值低于一定的显着性水平,则我们有足够的证据表明至少其中一个组均值与其他均值不同。
然而,这并没有告诉我们哪些群体彼此不同。这只是告诉我们并非所有组的平均值都是相等的。
为了准确地知道哪些组彼此不同,我们需要执行事后测试来控制每个族的错误率。
三种最常用的事后测试包括:
- 图基法
- 谢夫方法
- 邦费罗尼方法
本教程概述了每种方法,并说明了根据情况使用哪种事后测试。
图基法
当您想要在组之间进行成对比较时,应使用图基事后检验,即每组的样本量相等。
如果样本量不相等,您可以使用测试的修改版本,称为 Tukey-Kramer 测试。
术语“成对”意味着我们只想一次比较两组的平均值。
例如,假设我们有三组:A、B、C。
图基的事后检验使我们能够进行以下两两比较:
- µA = µB
- µA = µC
- μB = μC
请注意,对于k组,总共有k ( k -1)/2 种可能的成对比较。
谢夫方法
当我们希望在组均值之间进行所有可能的对比时,应使用 Scheffe 事后检验。与 Tukey 事后检验不同,此检验允许您一次比较两个以上的均值。
例如,假设我们有四个组:A、B、C、D。
Scheffe 事后测试将允许进行复杂的比较,例如:
- μA – μB = μC – μD
- μA + μD = μB + μC
尽管 Scheffe 事后检验是最灵活的,但它也是最保守的,并且产生最宽的置信区间。这意味着它具有最低的统计功效和最低的检测组间真实差异的能力。
请注意,无论组样本大小是否相等,都可以使用 Scheffe 事后检验。
邦费罗尼方法
当您想要提前执行一组计划的比较时,应使用 Bonferroni 事后测试。
例如,假设我们有三个组——A、B、C——并且我们事先知道我们只对以下比较感兴趣:
- µA = µB
- μB = μC
当我们有一组特定的计划比较并希望像这样提前执行时,Bonferroni 事后检验会产生最窄的置信区间,这意味着它具有最大的能力来检测兴趣组之间的真正差异。 。
请注意,无论组样本大小是否相等,也可以使用 Bonferroni 事后检验。
您应该使用哪种方法?
以下决策树可帮助您根据情况决定应使用哪种事后测试:
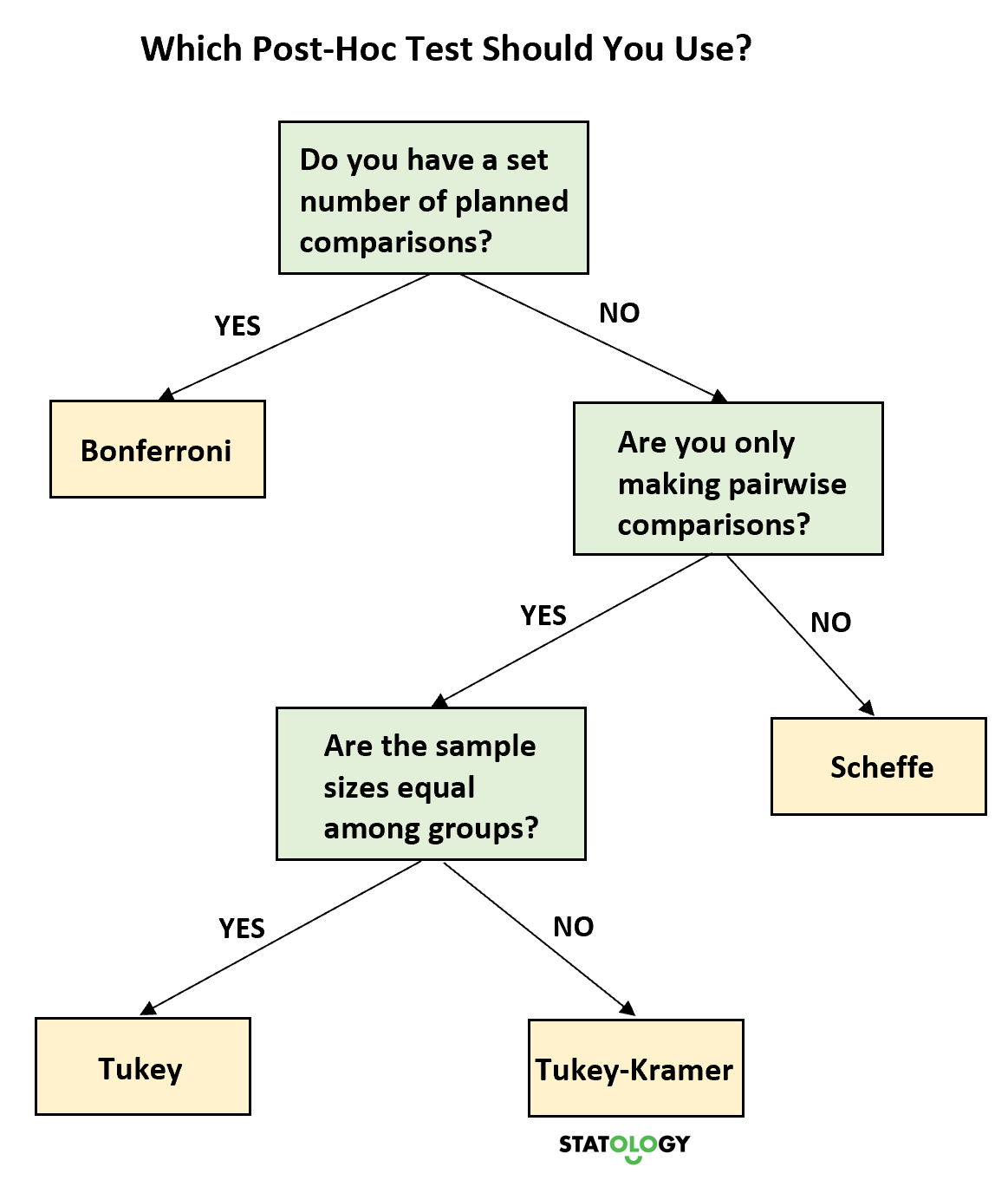
最后的想法
无论您选择使用哪种事后测试,您都必须在进行实验之前做出决定。
这会阻止您在实验后选择更有可能产生显着结果的事后测试,这被认为是不诚实的研究实践。
无论如何,大多数统计软件都能够执行这些事后测试,因此您很少需要手动计算它们。