如何在 r 中执行 tukey 测试
单向方差分析用于确定三个或更多独立组的平均值之间是否存在统计显着差异。
如果方差分析表的总体p 值低于一定的显着性水平,则我们有足够的证据表明至少其中一个组均值与其他均值不同。
然而,这并没有告诉我们哪些群体彼此不同。这只是告诉我们并非所有组的平均值都是相等的。为了准确地了解哪些组彼此不同,我们需要执行事后测试。
最常用的事后检验之一是Tukey 检验,它允许我们在每组均值之间进行成对比较,同时控制族错误率。
本教程介绍如何在 R 中执行 Tukey 测试。
注意:如果研究中的任何组被视为对照组,则应使用Dunnett 检验作为事后检验。
示例:R 中的 Tukey 测试
步骤 1:拟合方差分析模型。
以下代码展示了如何创建一个包含三组(A、B 和 C)的假数据集,并对数据拟合单向方差分析模型以确定每组的平均值是否相等:
#make this example reproducible set.seed(0) #create data data <- data.frame(group = rep (c("A", "B", "C"), each = 30), values = c(runif(30, 0, 3), runif(30, 0, 5), runif(30, 1, 7))) #view first six rows of data head(data) group values 1 A 2.6900916 2 A 0.7965260 3 A 1.1163717 4 A 1.7185601 5 A 2.7246234 6 A 0.6050458 #fit one-way ANOVA model model <- aov (values~group, data=data) #view the model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) group 2 98.93 49.46 30.83 7.55e-11 *** Residuals 87 139.57 1.60 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
我们可以看到方差分析表中的总体 p 值为7.55e-11 。由于这个数字小于0.05,我们有足够的证据表明每组中的平均值并不相等。因此,我们可以进行 Tukey 检验来准确确定哪些组均值不同。
步骤 2:执行 Tukey 测试。
以下代码显示如何使用TukeyHSD()函数执行 Tukey 测试:
#perform Tukey's Test TukeyHSD(model, conf.level= .95 ) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = values ~ group, data = data) $group diff lwr upr p adj BA 0.9777414 0.1979466 1.757536 0.0100545 CA 2.5454024 1.7656076 3.325197 0.0000000 CB 1.5676610 0.7878662 2.347456 0.0000199
p 值表示每个程序之间是否存在统计显着差异。结果显示,各方案的平均减肥效果在0.05显着性水平上存在统计学上的显着差异。
尤其:
- B 和 A 之间均值差异的 P 值: 0.0100545
- C 和 A 之间均值差异的 P 值: 0.0000000
- C 和 B 之间平均值差异的 P 值: 0.0000199
第 3 步:可视化结果。
我们还可以使用plot(TukeyHSD())函数来可视化置信区间:
#plot confidence intervals plot(TukeyHSD(model, conf.level= .95 ), las = 2 )
注意: las参数指定刻度标签必须垂直 (las=2) 轴。
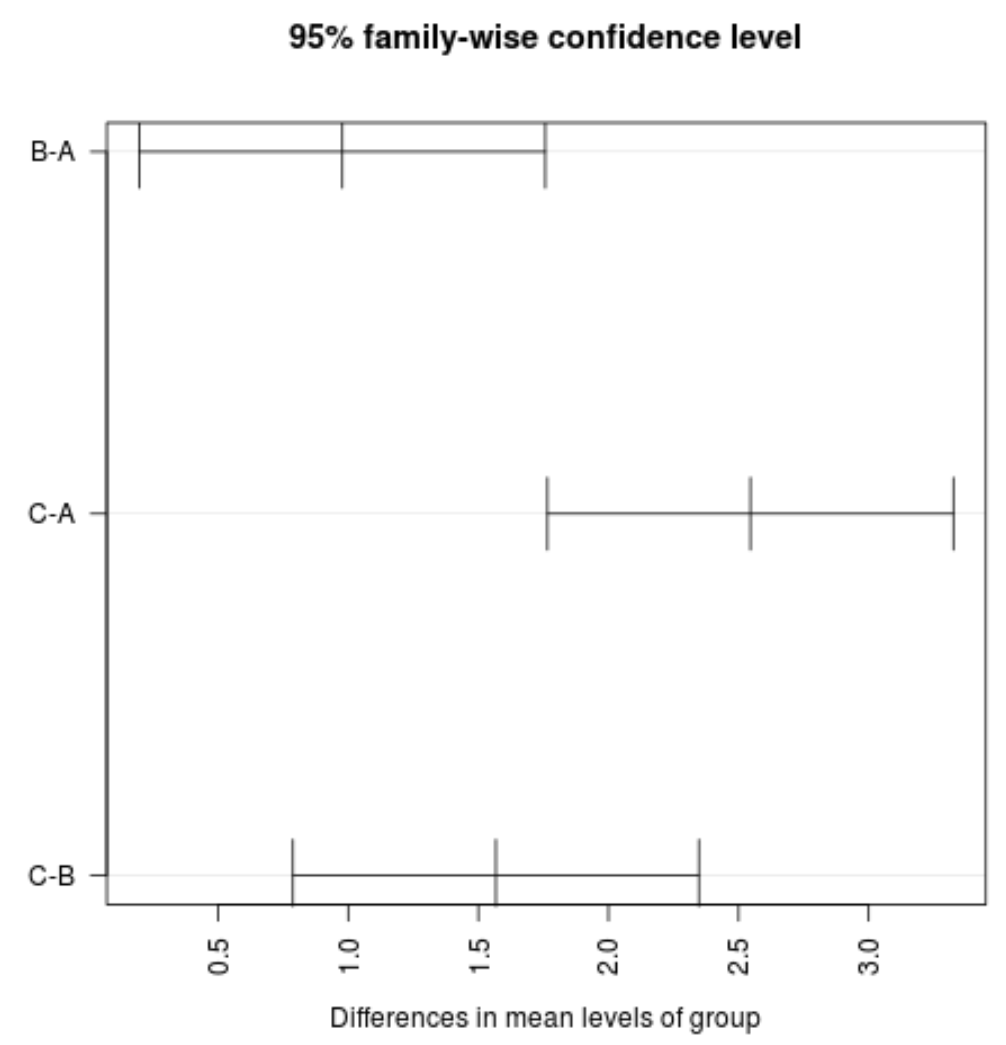
我们可以看到,组之间平均值的置信区间都不包含零值,这表明三组之间的平均损失存在统计显着差异。这与我们假设检验的所有 p 值均小于 0.05 一致。
对于这个特定的例子,我们可以得出以下结论:
- C组的平均值明显高于A组和B组的平均值。
- B组的平均值明显高于A组的平均值。