如何在 r 中绘制多元线性回归结果

当我们在 R 中执行简单线性回归时，很容易可视化拟合回归线，因为我们只使用单个预测变量和单个响应变量。

例如，以下代码显示如何将简单的线性回归模型拟合到数据集并绘制结果：

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

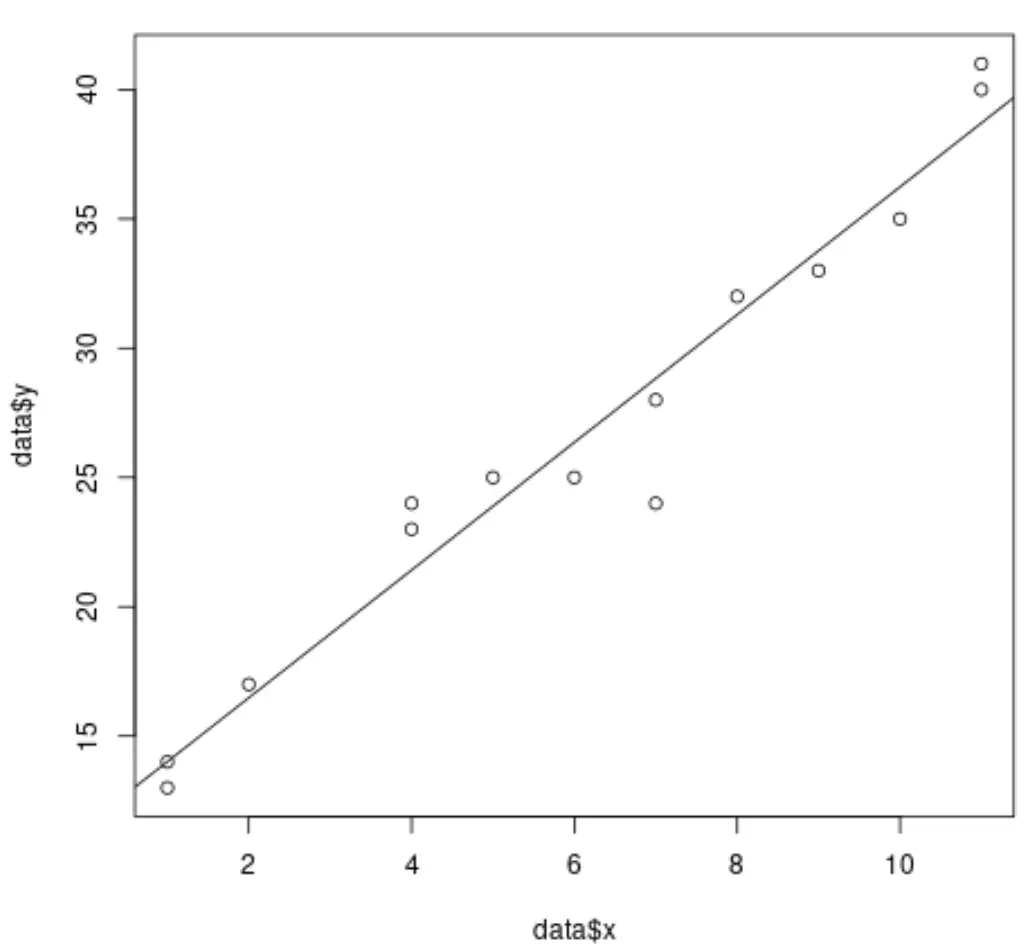
然而，当我们执行多元线性回归时，结果变得很难可视化，因为有多个预测变量，而且我们不能简单地在二维图上绘制回归线。

相反，我们可以使用添加变量图（有时称为“部分回归图”），它们是显示响应变量和预测变量之间关系的单独图，同时控制模型中其他预测变量的存在。

以下示例演示如何在 R 中执行多元线性回归并使用附加变量图可视化结果。

示例：在 R 中绘制多重线性回归结果

假设我们使用内置mtcars数据集将以下多元线性回归模型拟合到 R 中的数据集：

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

从结果中我们可以看到每个系数的 p 值都小于 0.1。为简单起见，我们假设每个预测变量都很重要并且应包含在模型中。

要生成附加变量的图，我们可以使用car包中的avPlots()函数：

 #load car package
library(car)

#produce added variable plots
avPlots(model)

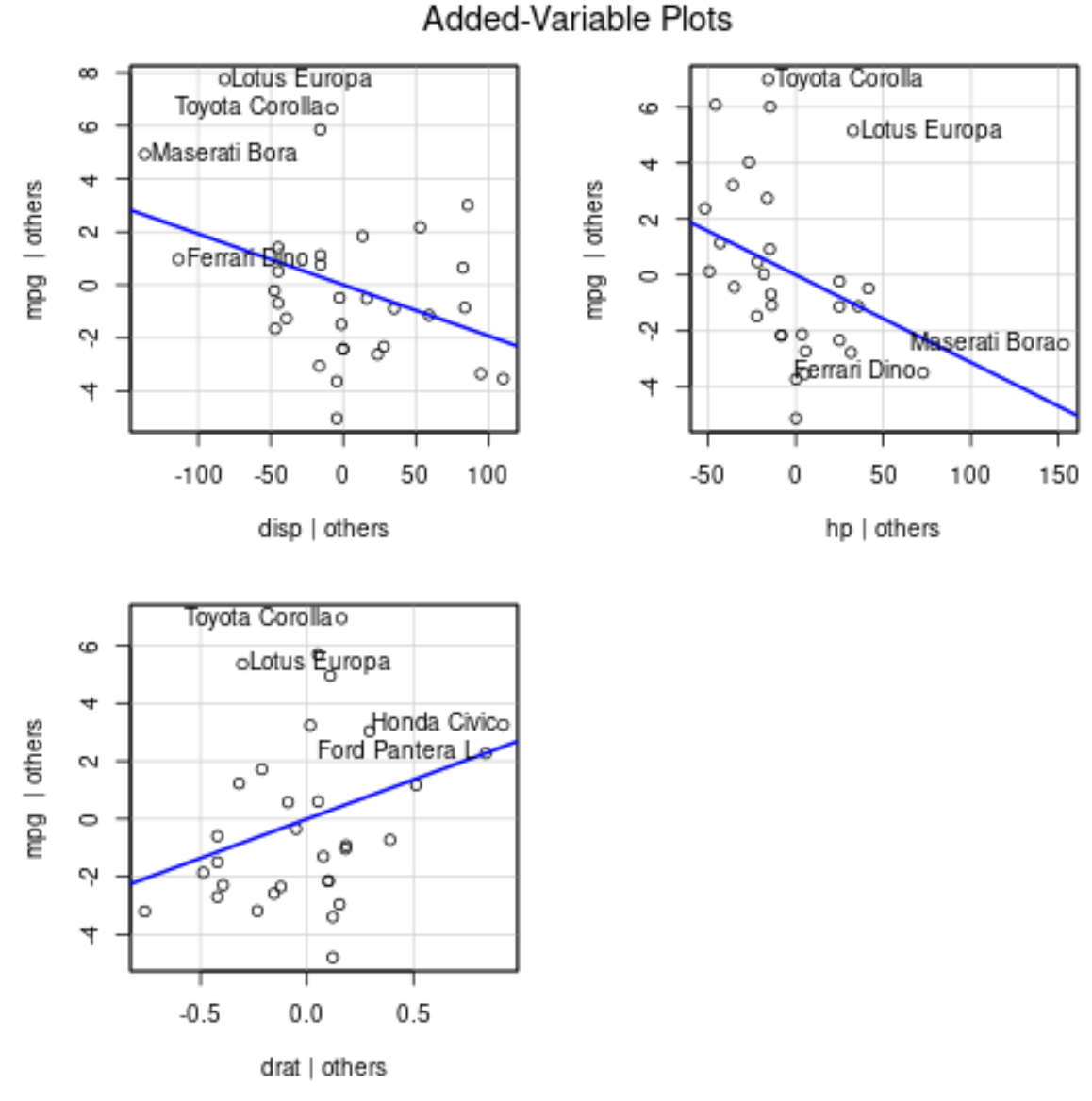
以下是如何解释每个情节：

• x 轴显示单个预测变量，y 轴显示响应变量。
• 蓝线显示预测变量和响应变量之间的关联，同时保持所有其他预测变量的值恒定。
• 每个图中的标记点代表具有最大残差的 2 个观测值和具有最大部分杠杆的 2 个观测值。

请注意，每个图中线条的角度对应于估计回归方程的系数的符号。

例如，以下是模型中每个预测变量的估计系数：

• 显示： -0.019232
• 通道： -0.031229
• 日期： 2.714975

请注意，在添加的变量图中， drat的线角度为正，而disp和hp的线角度为负，这对应于它们估计系数的符号：

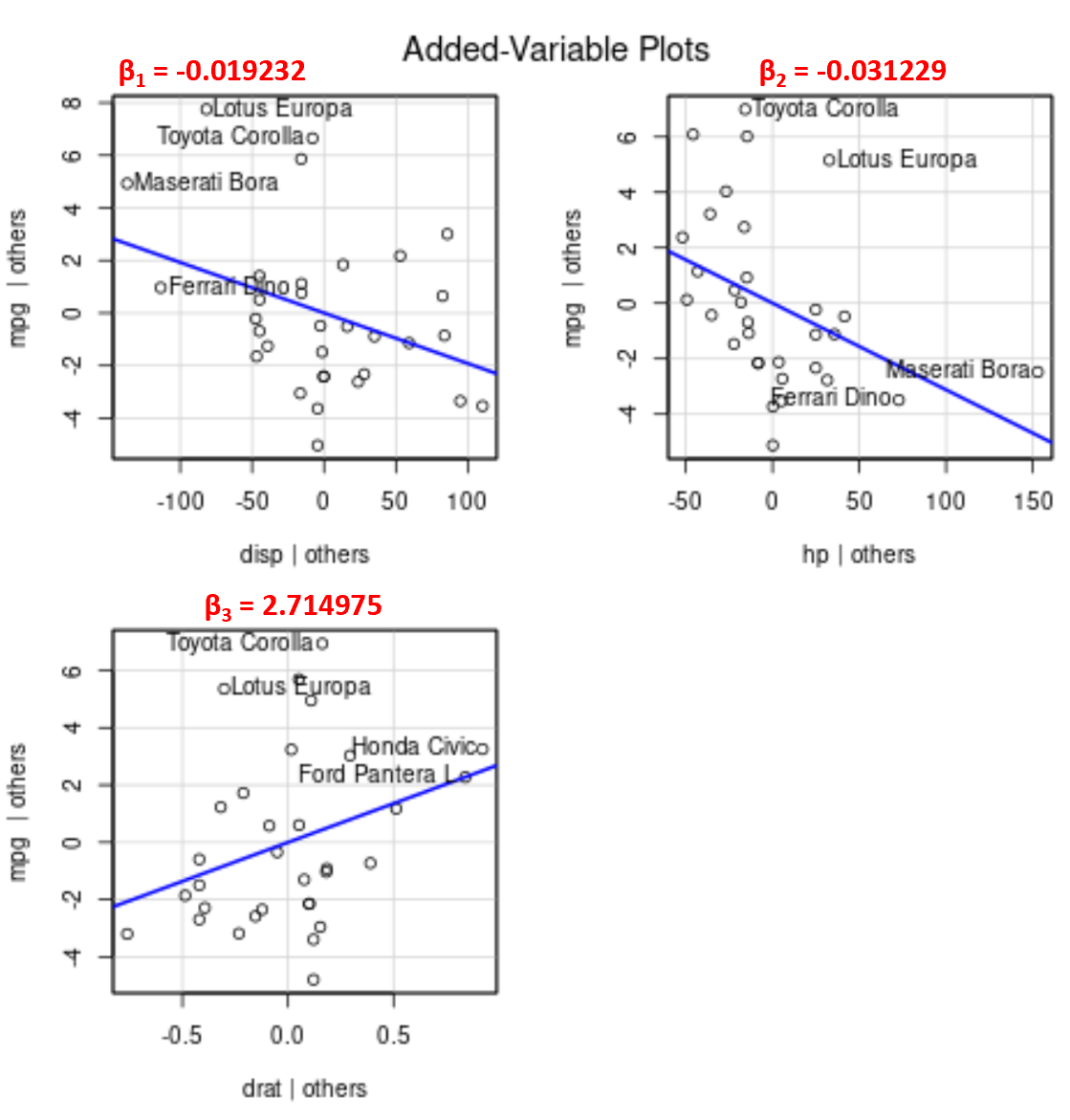
虽然我们无法在二维图上绘制一条拟合回归线，因为我们有多个预测变量，但这些添加的变量图使我们能够观察每个单独的预测变量和响应变量之间的关系，同时保持其他预测变量不变。