完整指南：如何检查多元方差分析假设
MANOVA （多变量方差分析）用于分析一个或多个因素变量如何影响多响应变量。
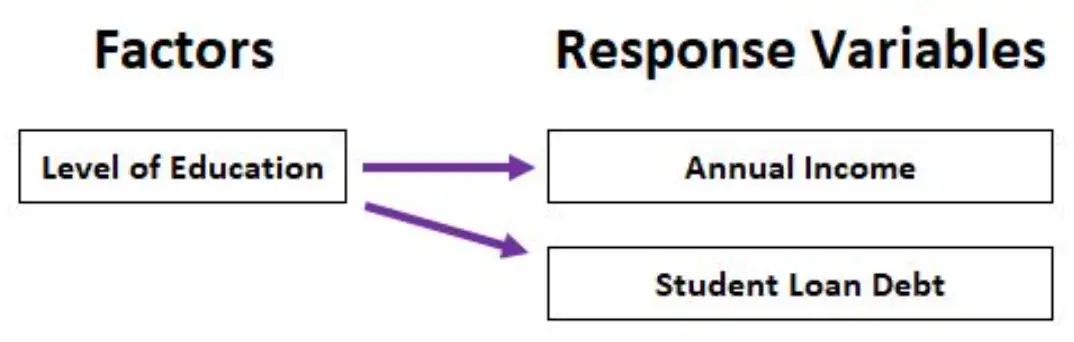
例如，我们可以使用多元方差分析来分析教育水平（高中文凭、副学士学位、学士学位、硕士学位）如何影响年收入和学生贷款债务总额。
相关： ANOVA、ANCOVA、MANOVA 和 MANCOVA 之间的区别
每次执行多元方差分析时，我们都必须验证是否满足以下假设：
1. 多元正态性– 响应变量在每组因子变量内呈多元正态分布。
2. 独立性——每个观察结果都是从总体中随机、独立抽样的。
3. 等方差——各组的总体协方差矩阵相等。
4. 没有多元异常值——不存在极端的多元异常值。
在本文中，我们对每个假设以及如何确定假设是否满足进行了解释。
假设 1：多元正态性
多元方差分析假设响应变量在每组因子变量内呈多元正态分布。
如果每个因子 * 响应变量组合至少有 20 个观测值，那么我们可以假设满足多元正态性假设。
如果每个因子*响应变量组合的观测值少于 20 个，我们可以创建散点图矩阵来可视化残差并直观地检查是否满足此假设。
幸运的是，众所周知，多元方差分析对于多元正态性的偏差具有鲁棒性，因此小到中等的偏差通常不是问题。
假设2：独立性
多元方差分析假设每个观测值都是从总体中随机且独立地抽样的。
只要使用概率抽样方法（总体中的每个成员都有相同的概率被选择进入样本）来收集数据，我们就可以假设每个观察值都是以随机且独立的方式进行抽样的。
概率抽样方法的示例包括：
- 简单随机抽样
- 分层随机抽样
- 随机整群抽样
- 系统随机抽样
假设 3：方差相等
多元方差分析假设每组的总体协方差矩阵相等。
检验这一假设的最常见方法是使用 Box 的 M 检验。已知该检验相当严格，这就是为什么我们通常使用 0.001 的显着性水平来确定总体协方差矩阵是否相等。
如果 Box 的 M 检验的 p 值大于 0.001，我们可以假设满足此假设。
幸运的是，即使检验的 p 值小于 0.001，多元方差分析对于与该假设的偏差也往往具有稳健性。
对于不等协方差矩阵来说，协方差矩阵之间的差异必须非常极端。
假设 4：没有多元异常值
多元方差分析假设数据中不存在可能显着影响结果的极端多元异常值。
验证此假设的最常见方法是计算每个观测值的马氏距离，它表示多元空间中两点之间的距离。
如果观测值的马哈拉诺比斯距离的相应 p 值小于 0.001，我们通常会声明该观测值是极端异常值。
参考以下教程，了解如何在各种统计软件中计算马哈拉诺比斯距离：
其他资源
以下教程解释了如何在各种统计软件中执行多元方差分析：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多