如何在 excel 中执行多元线性回归

多元线性回归是一种我们可以用来理解两个或多个解释变量与响应变量之间关系的方法。

本教程介绍如何在 Excel 中执行多元线性回归。

注意：如果只有一个解释变量，则应该执行简单的线性回归。

示例：Excel 中的多元线性回归

假设我们想知道学习时间和参加预科考试的次数是否会影响学生在某次高考中的成绩。

为了探索这种关系，我们可以使用学习时间和准备考试作为解释变量，并使用考试结果作为响应变量来执行多元线性回归。

在 Excel 中完成以下步骤以执行多元线性回归。

第 1 步：输入数据。

输入 20 名学生的学习时数、参加的预备考试和收到的考试结果的以下数据：

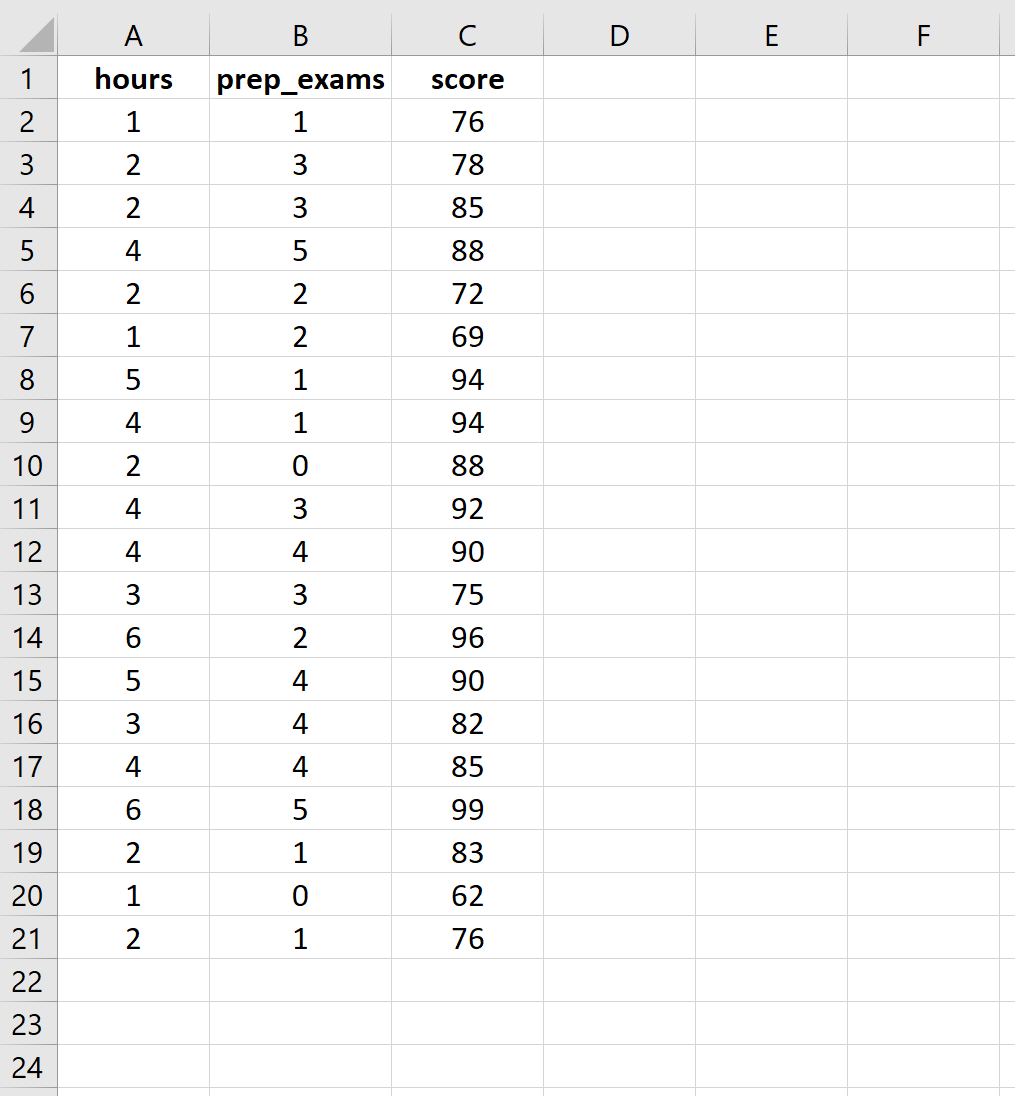
步骤 2：执行多元线性回归。

在 Excel 的顶部功能区上，转到“数据”选项卡，然后单击“数据分析” 。如果您没有看到此选项，则必须首先安装免费的分析工具库软件。

单击“数据分析”后，将出现一个新窗口。选择回归并单击确定。

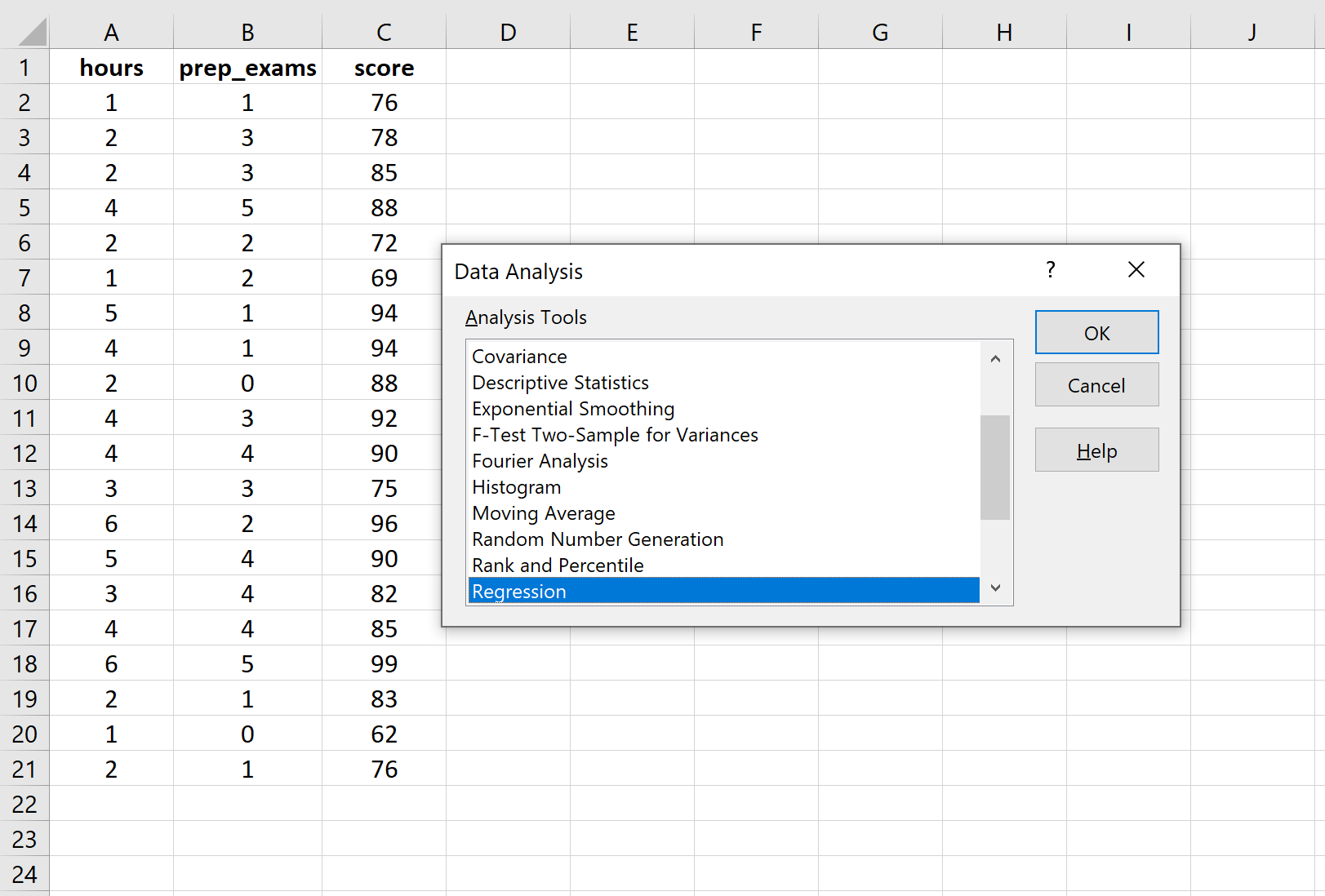
对于输入 Y 范围，填写响应变量的值数组。对于输入 X 范围，填写两个解释变量的值数组。选中“标签”旁边的框，让 Excel 知道我们已将变量名称包含在输入范围中。对于输出范围，选择要在其中显示回归输出的单元格。然后单击“确定” 。

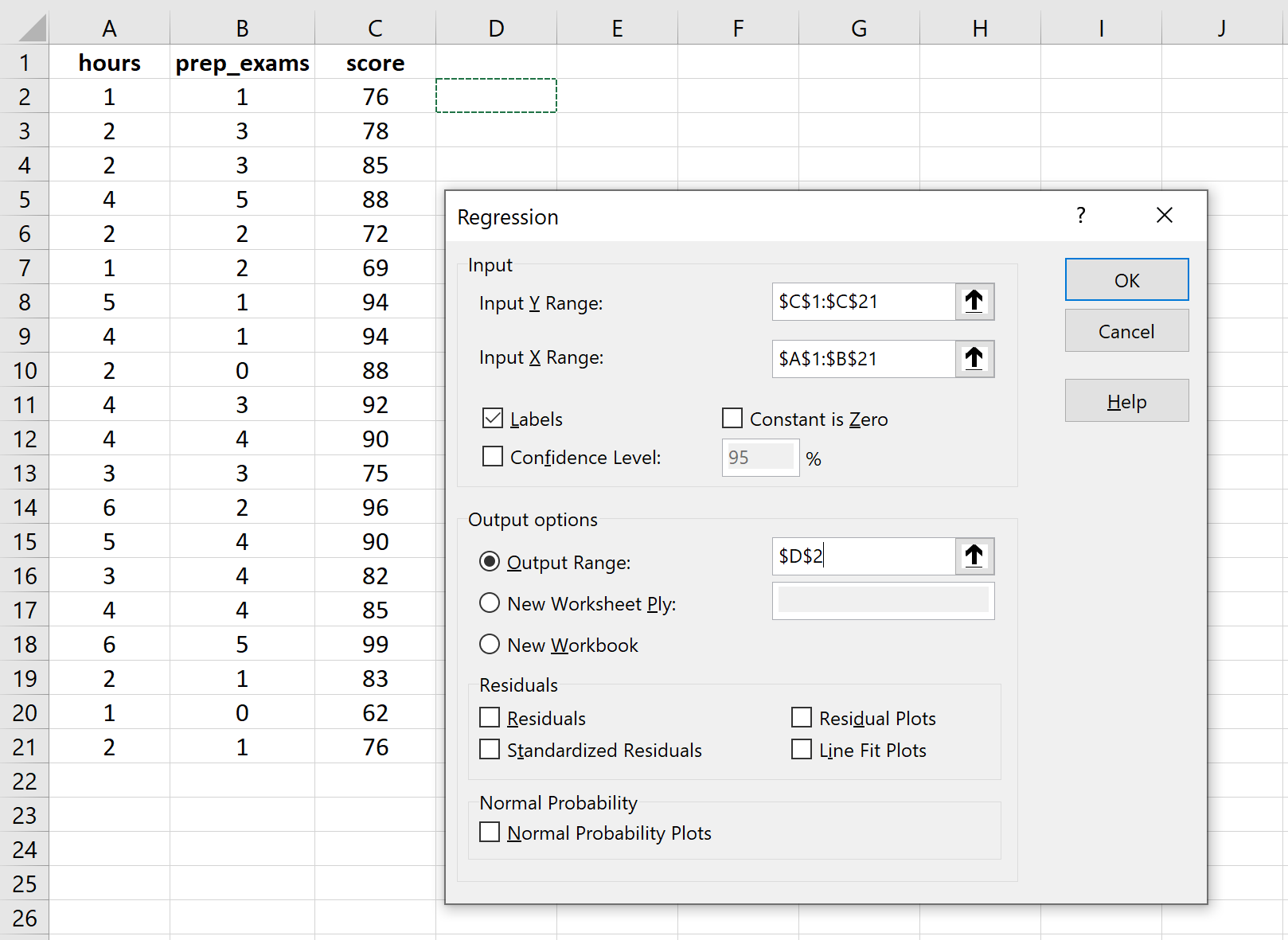
将自动出现以下输出：

步骤 3：解释结果。

以下是如何解释结果中最相关的数字：

R 方： 0.734 。这称为决定系数。它是响应变量的方差可以被解释变量解释的比例。在此示例中，73.4% 的考试成绩差异是由学习时数和参加的准备考试次数来解释的。

标准误差： 5.366 。这是观测值与回归线之间的平均距离。在此示例中，观测值与回归线平均偏差 5,366 个单位。

F： 11:46 pm这是回归模型的总体 F 统计量，计算为回归 MS/残余 MS。

含义 F：0.0000 。这是与总体 F 统计量相关的 p 值。这告诉我们回归模型作为一个整体是否具有统计显着性。换句话说，它告诉我们两个解释变量的组合是否与响应变量具有统计上显着的关联。在这种情况下，p 值小于 0.05，表明解释变量、学习时间和参加的准备考试相结合，与考试结果具有统计显着相关性。

P 值。各个 p 值告诉我们每个解释变量是否具有统计显着性。我们可以看到，学习时间具有统计显着性 (p = 0.00)，而参加的预备考试(p = 0.52) 在 α = 0.05 时不具有统计显着性。由于过去的预备考试在统计上不显着，我们最终可能决定将其从模型中删除。

系数：假设其他解释变量保持不变，每个解释变量的系数告诉我们响应变量的预期平均变化。例如，假设练习考试保持不变，学习时间每增加一小时，平均考试成绩预计会增加5.56 分。

还有另一种看待方式：如果学生 A 和学生 B 参加的预科考试次数相同，但学生 A 多学习一个小时，那么学生 A 的得分应该比学生 B 高5.56分。

我们将截距系数解释为不学习任何时间且不参加预备考试的学生的预期考试成绩为67.67 。

估计回归方程：我们可以使用模型输出的系数来创建以下估计回归方程：

考试成绩 = 67.67 + 5.56*(小时) – 0.60*(预备考试)

我们可以使用这个估计的回归方程根据学生的学习小时数和参加练习考试的次数来计算学生的预期考试成绩。例如，学习三个小时并参加预备考试的学生应该得到83.75的成绩：

考试成绩 = 67.67 + 5.56*(3) – 0.60*(1) = 83.75

请记住，由于过去的准备考试在统计上不显着 (p=0.52)，我们可能会决定删除它们，因为它们不会对整体模型提供任何改进。在这种情况下，我们可以仅使用研究的时间作为解释变量来执行简单的线性回归。

可以在此处找到此简单线性回归分析的结果。

其他资源

执行多元线性回归后，您可能需要检查几个假设，包括：

1.使用 VIF 测试多重共线性。

2. 使用 Breusch-Pagan 检验检验异方差性。

3.使用 QQ 图检验正态性。