什么是多式联运？

多峰分布是具有两种或多种模式的概率分布。

如果您创建直方图来可视化多峰分布，您会注意到它有几个峰值：

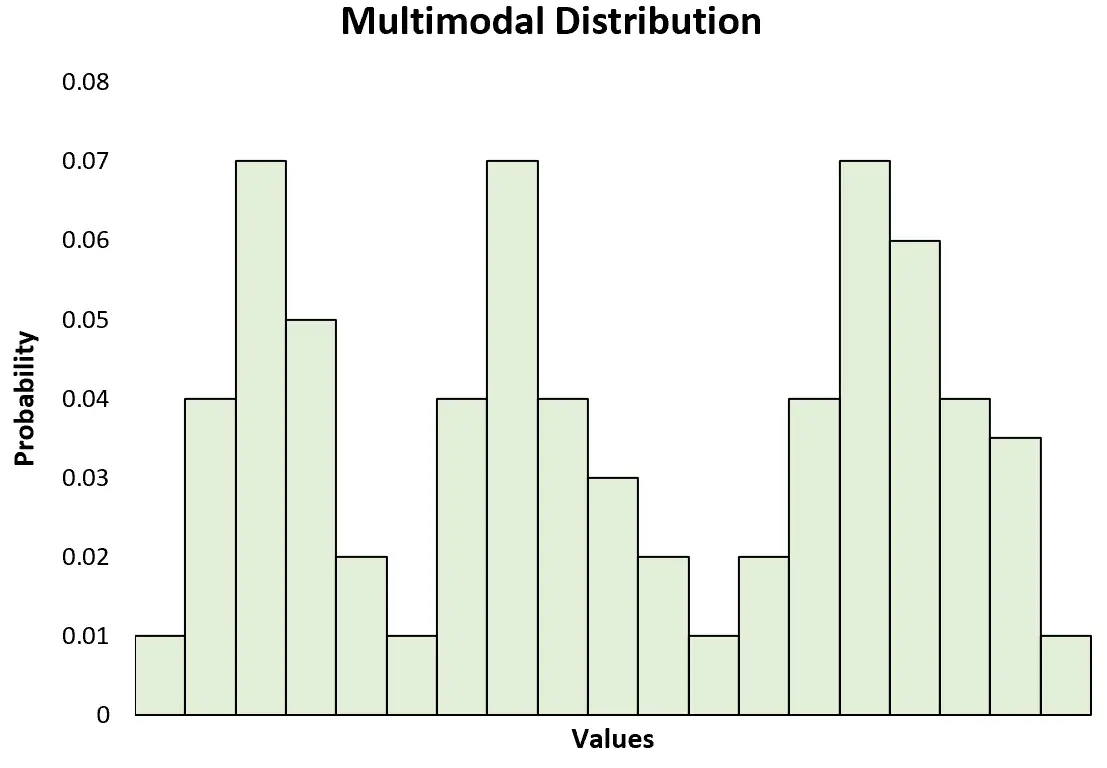
如果分布恰好有两个峰值，则将其视为双峰分布，这是多峰分布的特定类型。

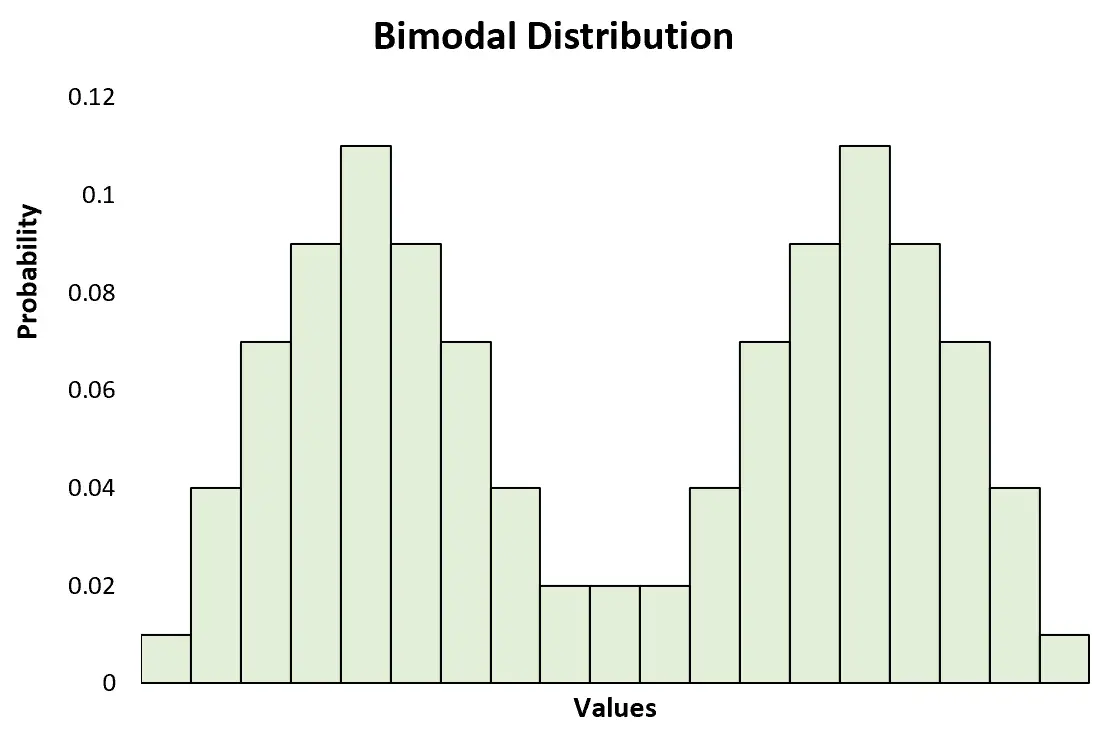
这与只有一个峰值的单峰分布形成对比：

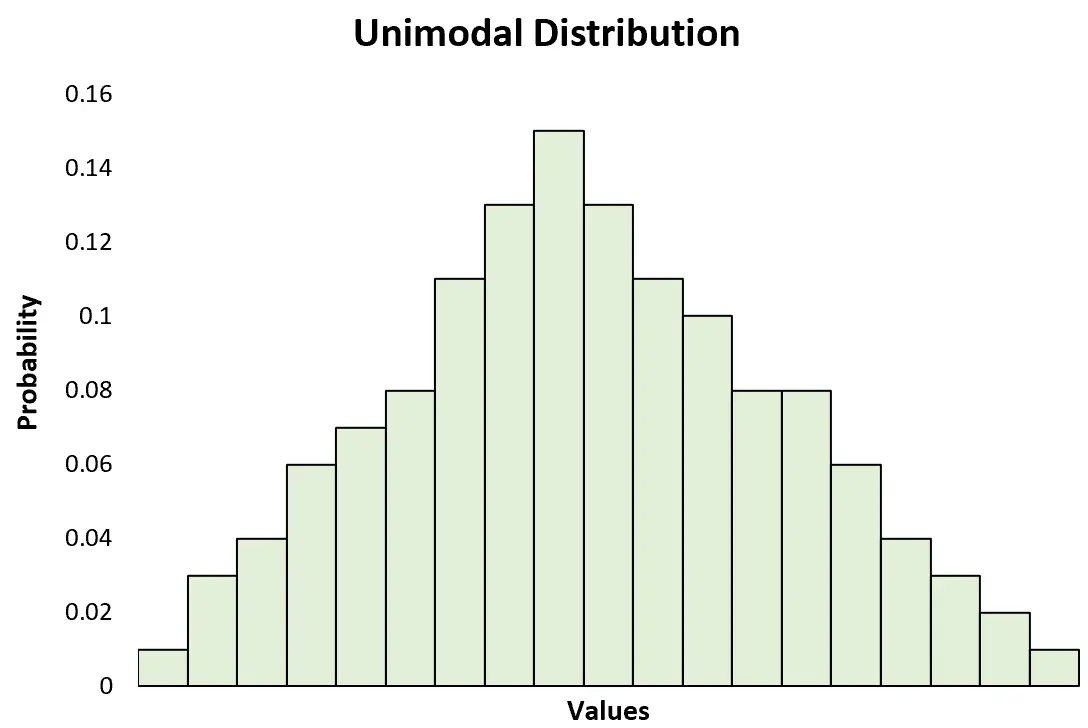
尽管像正态分布这样的单峰分布最常用于解释统计学中的主题，但多峰分布实际上在实践中经常出现，因此了解如何识别和分析它们是很有用的。

多峰分布的示例

以下是多峰分布的一些示例。

示例 1：考试成绩分布

假设一位教授给他的班级进行考试。有些学生学习了，有些则没有。当教授创建考试成绩直方图时，它遵循多模态分布，其中未学习的学生的低分附近有一个峰值，而学习过的学生的高分周围有另一个峰值：

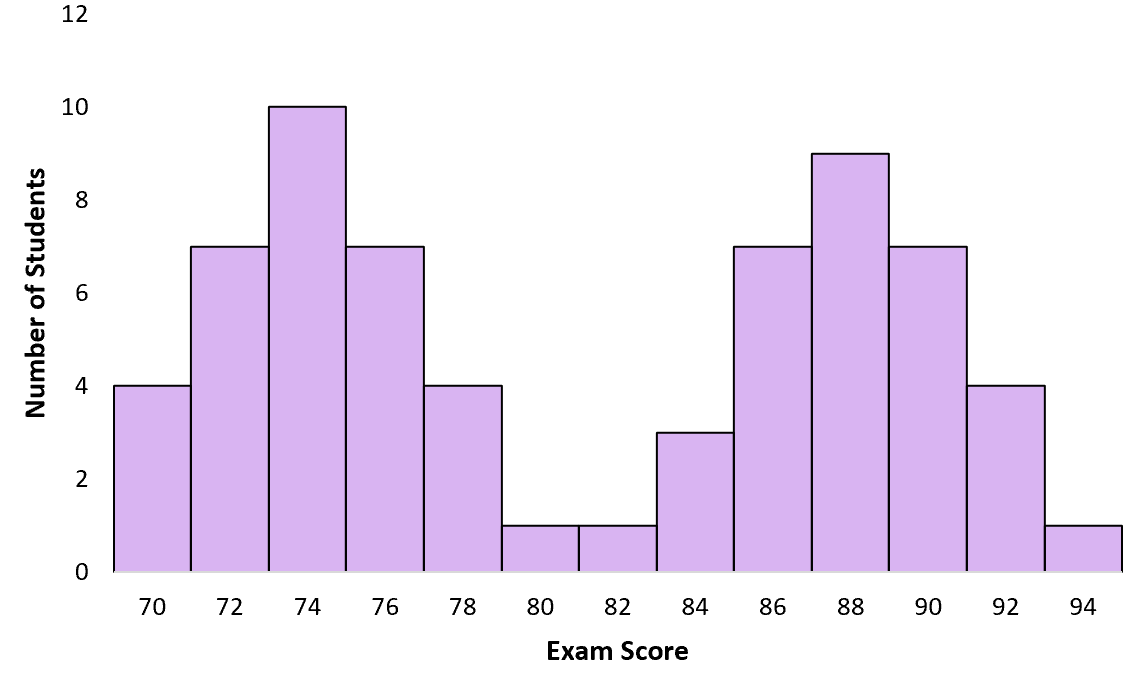
示例2：不同植物种类的高度

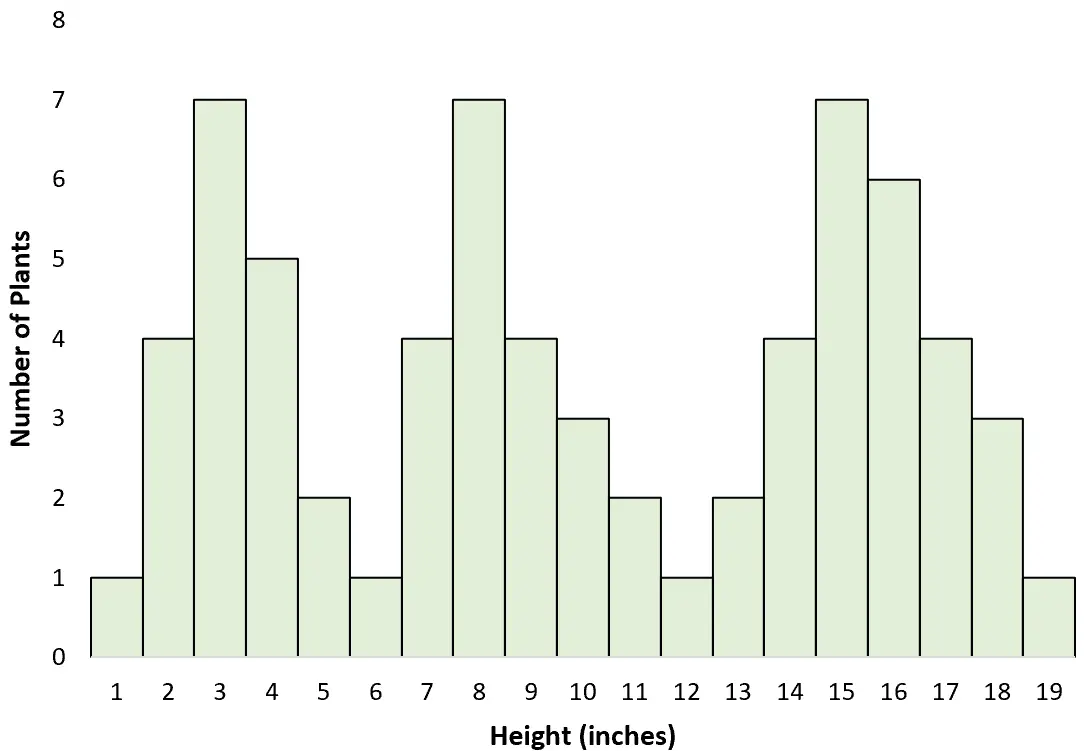
假设一位科学家绕着田地走动并测量不同植物的高度。她没有意识到，测量了三种不同物种的大小：一种很大，另一种中等大小，另一种很小。

当她创建直方图来可视化高度分布时，她发现它是多峰的：每个峰代表三个不同物种最常见的高度。

示例3：客户分布

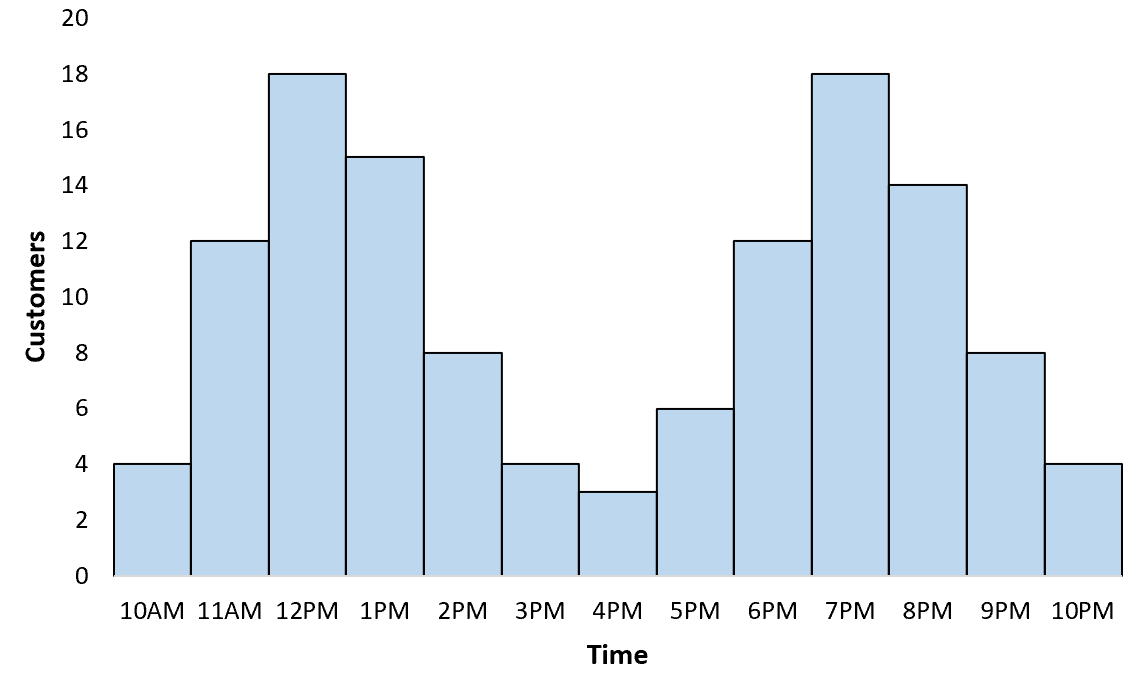
一家餐馆老板跟踪每小时光顾的顾客数量。当他创建直方图来可视化客户分布时，他发现分布是多峰的：午餐时间有一个峰值，晚餐时间有另一个峰值。

多峰分布的原因是什么？

多峰分布通常有以下两个原因之一：

1. 几个组被分组在一起。

当您在没有意识到的情况下收集多个组的数据时，可能会发生多模态分布。

例如，如果科学家在不知情的情况下测量了同一田地中三种不同植物物种的高度，则所有植物的分布在放置在同一直方图上时将呈现多峰分布。

2.有一个潜在的现象。

由于某些潜在现象，也可能会出现多峰分布。

例如，每小时光临餐厅的顾客数量遵循多模式分布，因为人们倾向于在两个不同的时间在餐厅吃饭：午餐和晚餐。这种潜在的人类行为是多模式分布的起源。

如何分析多峰分布

我们经常使用平均值或中位数来描述分布，因为这让我们知道分布的“中心”在哪里。

不幸的是，对于双峰分布来说，平均值和中位数没有什么用处。例如，上例中学生的平均考试成绩为81：

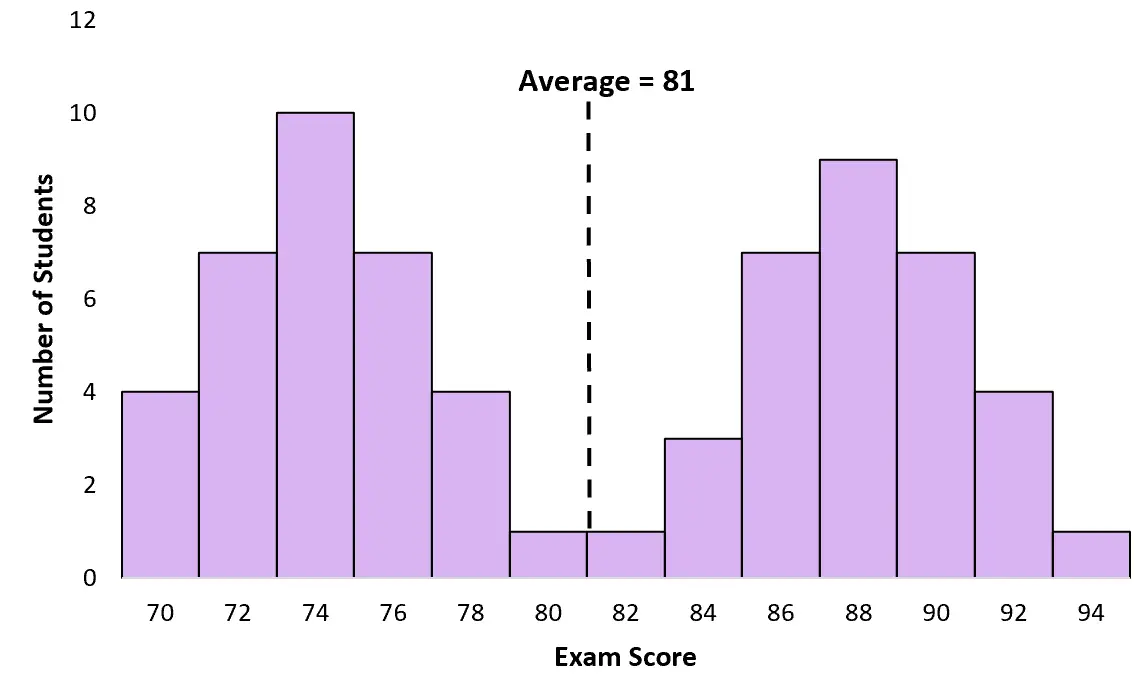
然而，很少有学生得分接近 81 分。在这种情况下，平均值具有误导性。大多数学生实际上得分在 74 或 88 左右。

分析和解释双峰分布的更好方法是简单地将数据分为两个不同的组，然后单独分析每个组的中心位置和分布。

例如，我们可以将考试成绩分为“低分”和“高分”，然后找到每组的平均值和标准差。

在计算给定分布（例如平均值、中位数或标准差）的汇总统计量时，请务必可视化分布以确定它是单峰还是多峰。

如果分布是多峰的，则使用单个平均值、中位数或标准差来描述它可能会产生误导。