R 倍数或 r 平方：有什么区别？

当您使用大多数统计软件拟合回归模型时，您经常会注意到结果中存在以下两个值：

Multiple R：三个或更多变量之间的多重相关系数。

R 方：计算公式为 (Multiple R) ² ，表示回归模型的响应变量中可由预测变量解释的方差比例。该值在 0 到 1 之间变化。

在实践中，我们经常对 R 平方值感兴趣，因为它告诉我们预测变量在预测响应变量值方面有多么有用。

然而，每次我们向模型添加新的预测变量时，即使预测变量没有用，R 方也一定会增加。

调整后的 R 平方是 R 平方的修改版本，可根据回归模型中的预测变量数量进行调整。计算方法如下：

调整后的 R ² = 1 – [(1-R ² )*(n-1)/(nk-1)]

金子：

• R ² ：模型的R ²
• n ：观察次数
• k ：预测变量的数量

由于当您向模型中添加更多预测变量时，R 平方总是会增加，因此调整后的 R 平方可以作为一个指标，告诉您模型的有用性，并根据模型中预测变量的数量进行调整。

为了更好地理解每个术语，请考虑以下示例。

示例：多重 R、R 平方和调整的 R 平方

假设我们有以下数据集，其中包含 12 名不同学生的以下三个变量：

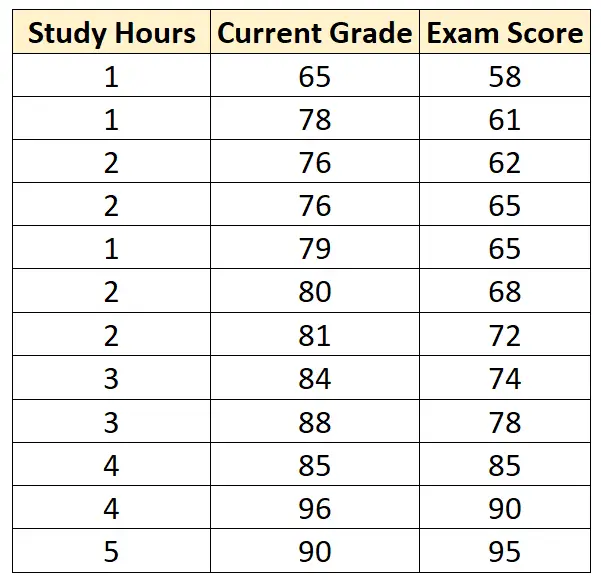
假设我们使用学习时间和当前成绩作为预测变量，考试成绩作为响应变量来拟合多元线性回归模型，并得到以下结果：

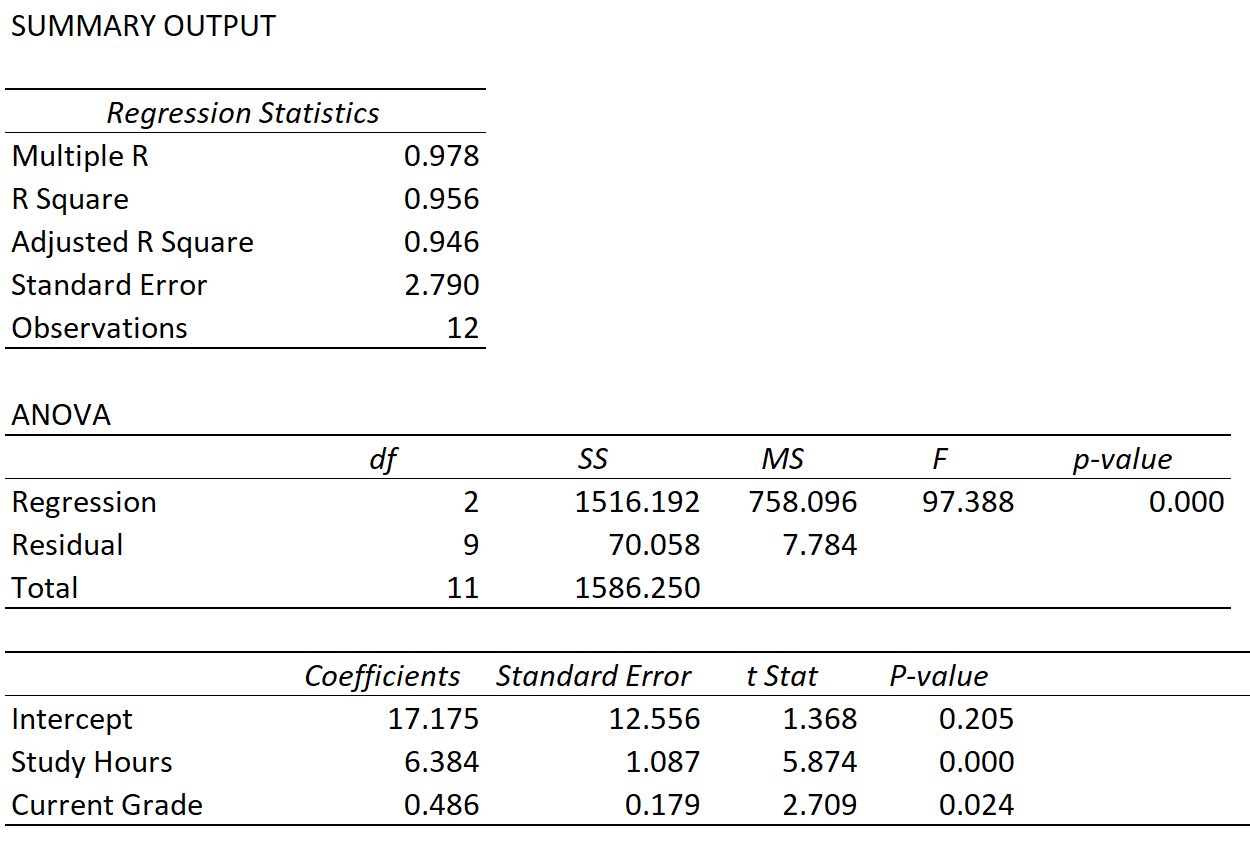
我们可以观察以下三个指标的值：

倍数 R：0.978 。这表示响应变量和两个预测变量之间的多重相关性。

R 方：0.956 。计算公式为 (Multiple R) ² = (0.978) ² = 0.956。这告诉我们，95.6% 的考试成绩差异可以通过学生学习的小时数和当前课程成绩来解释。

调整后的 R 平方：0.946 。计算如下：

调整后的 R ² = 1 – [(1-R ² )*(n-1)/(nk-1)] = 1 – [(1-.956)*(12-1)/(12-2-1) ] = 0.946。

这表示 R 平方值，根据模型中预测变量的数量进行调整。

例如，如果我们拟合另一个具有 10 个预测变量的回归模型，并发现该模型的调整后 R 平方为0.88 ，则此度量将很有用。这表明只有两个预测变量的回归模型更好，因为它具有更高的调整 R 平方值。

其他资源

多元线性回归简介
什么是好的 R 平方值？