R 中的多项式回归（逐步）

当预测变量和响应变量之间的关系是非线性时，可以使用多项式回归技术。

这种类型的回归采用以下形式：

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

其中h是多项式的“次数”。

本教程提供了如何在 R 中执行多项式回归的分步示例。

第 1 步：创建数据

在此示例中，我们将创建一个数据集，其中包含 50 名学生的班级的学习小时数和期末考试成绩：

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

第 2 步：可视化数据

在将回归模型拟合到数据之前，我们首先创建一个散点图来可视化学习时间和考试成绩之间的关系：

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

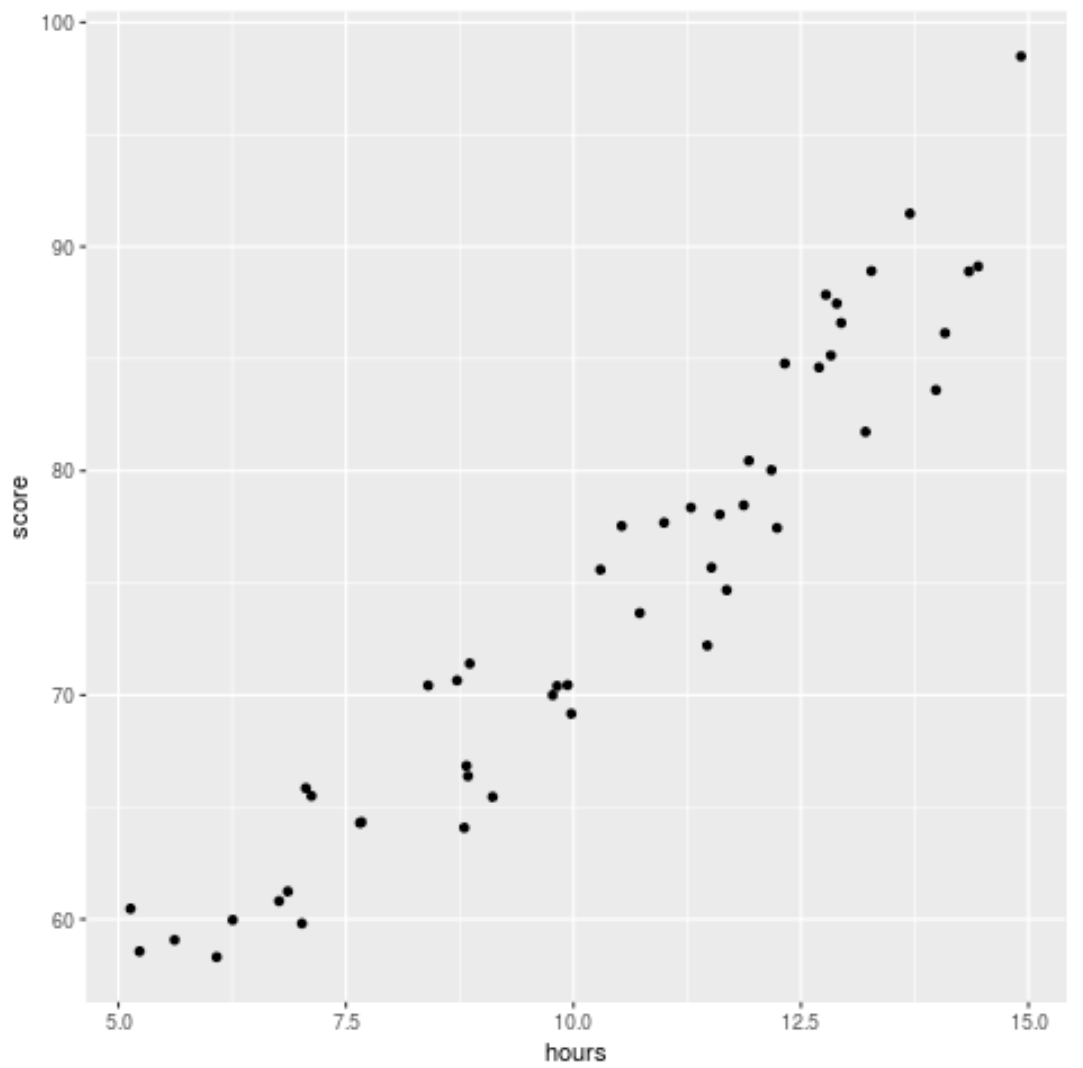
我们可以看到数据具有轻微的二次关系，表明多项式回归可能比简单线性回归更好地拟合数据。

步骤 3：拟合多项式回归模型

接下来，我们将拟合五个不同的多项式回归模型，其次数h = 1…5，并使用 k = 10 次的 k 倍交叉验证来计算每个模型的 MSE 检验：

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

从结果中我们可以看到每个模型的MSE测试：

• h 度 = 1 的 MSE 检验： 9.80
• h 度 = 2 的 MSE 检验： 8.75
• h 度 = 3 的 MSE 检验： 9.60
• h 度 = 4 的 MSE 检验： 10.59
• h 度 = 5 的 MSE 检验： 13.55

测试 MSE 最低的模型是次数h = 2 的多项式回归模型。

这符合我们对原始散点图的直觉：二次回归模型最适合数据。

第四步：分析最终模型

最后，我们可以获得表现最好的模型的系数：

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

从结果中我们可以看出，最终的拟合模型为：

分数 = 54.00526 – 0.07904*（小时）+ 0.18596*（小时） ²

我们可以使用这个方程来估计学生根据学习小时数将获得的分数。

例如，学习 10 小时的学生应该得到71.81的成绩：

分数 = 54.00526 – 0.07904*(10) + 0.18596*(10) ² = 71.81

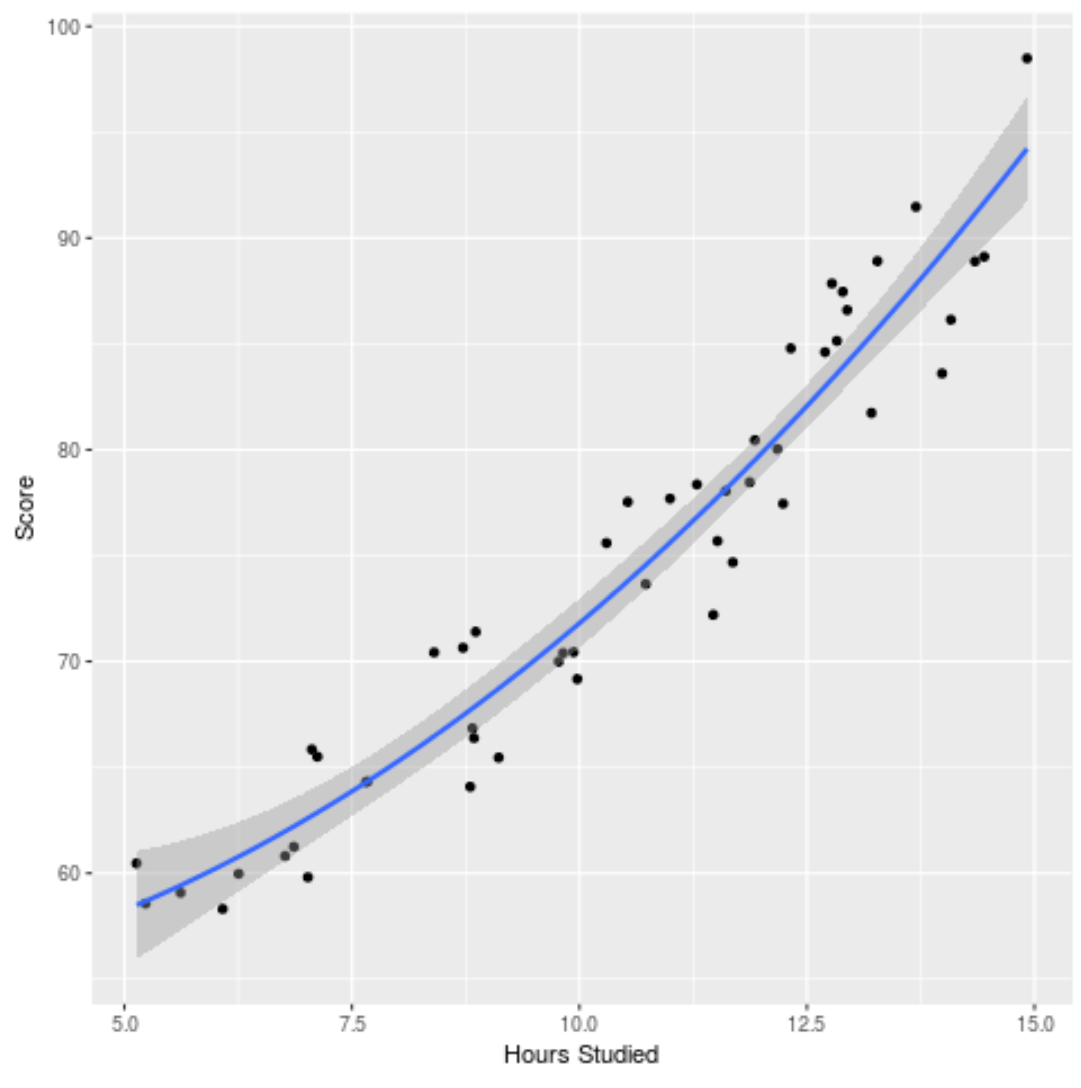
我们还可以绘制拟合模型来查看它与原始数据的拟合程度：

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

您可以在此处找到本示例中使用的完整 R 代码。