Google 表格中的多项式回归（逐步）

回归分析用于量化一个或多个预测变量与响应变量之间的关系。

最常见的回归分析类型是简单线性回归，当预测变量和响应变量具有线性关系时使用。

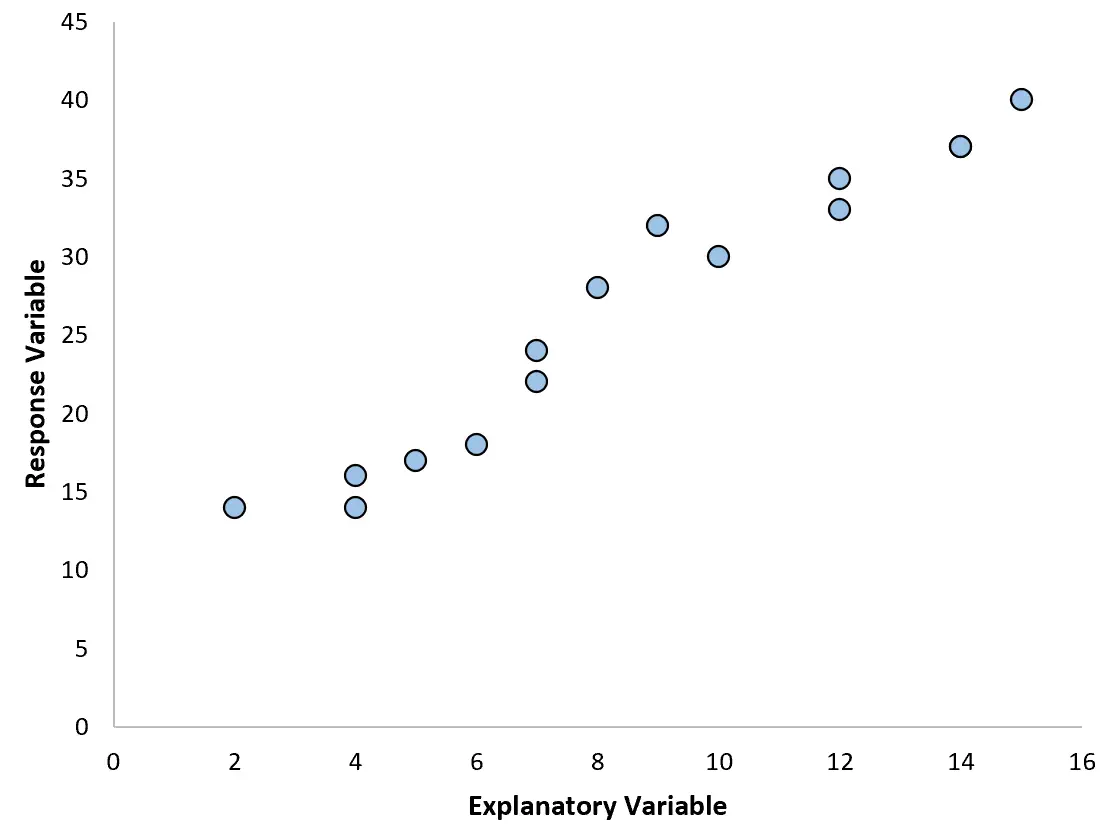
然而，有时预测变量和响应变量之间的关系是非线性的。

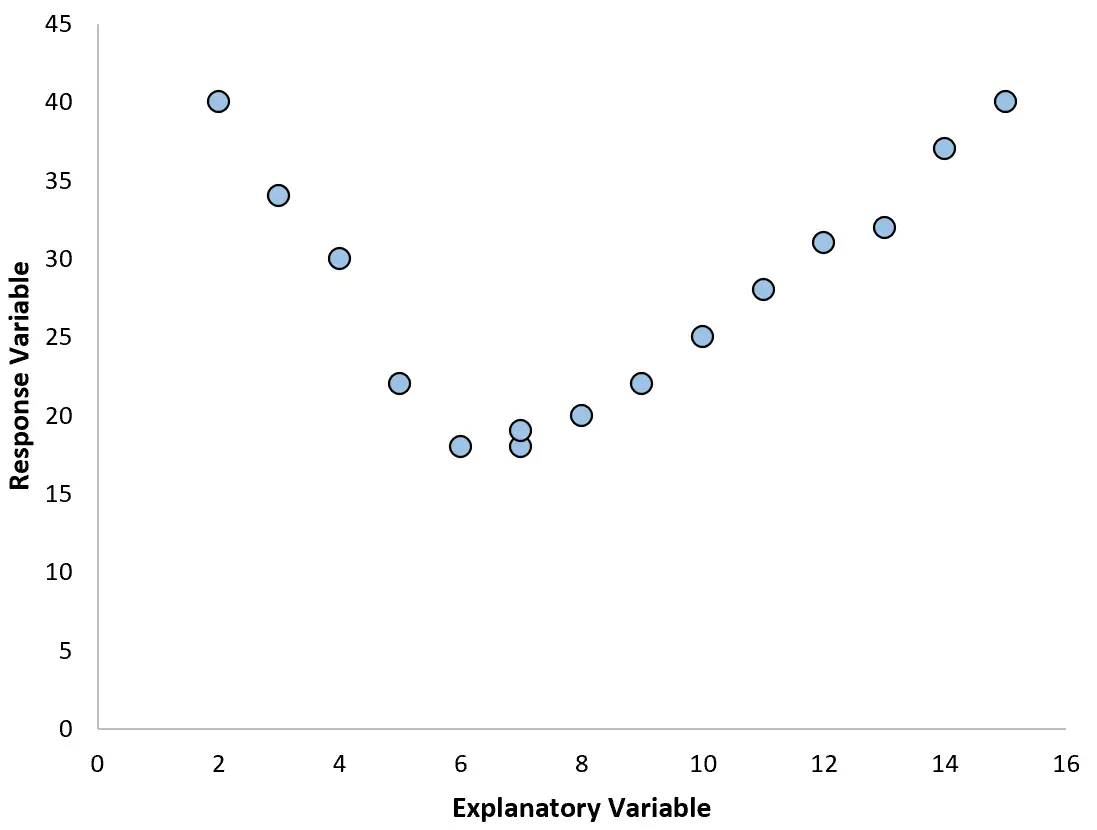
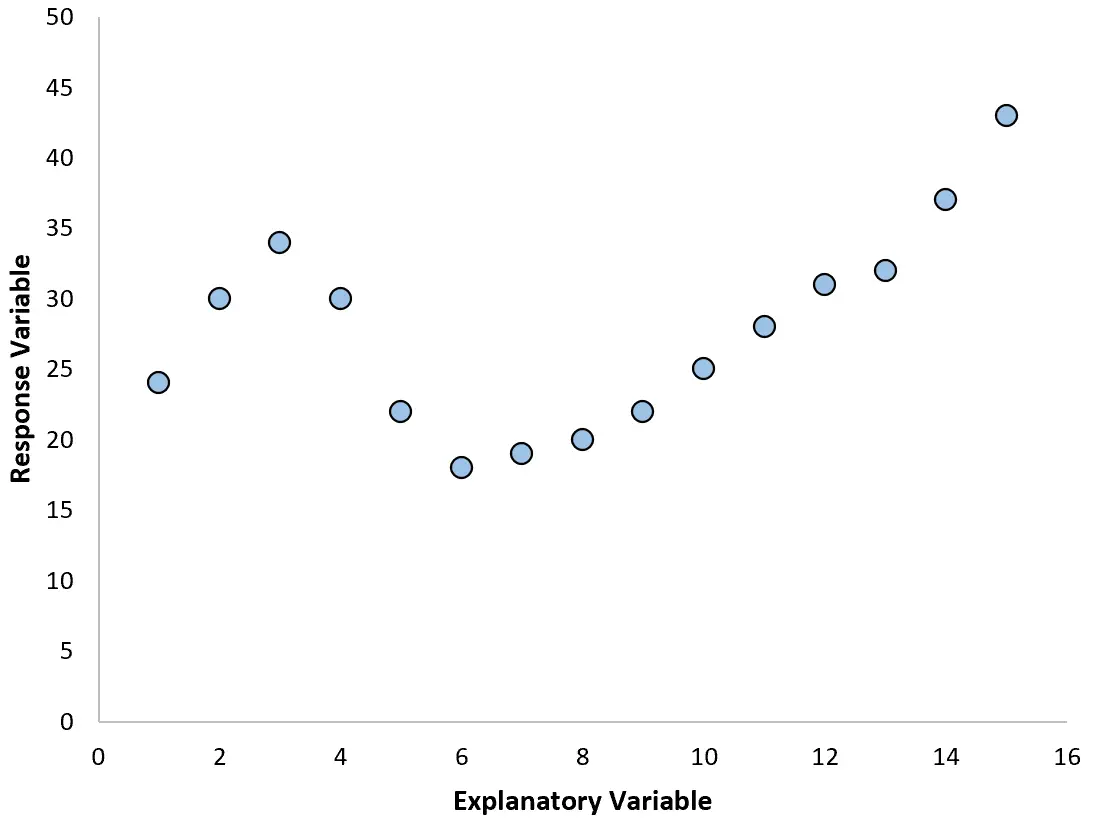
在这些情况下，使用多项式回归是有意义的，它可以解释变量之间的非线性关系。

本教程提供了如何在 Google 表格中执行多项式回归的分步示例。

第 1 步：创建数据

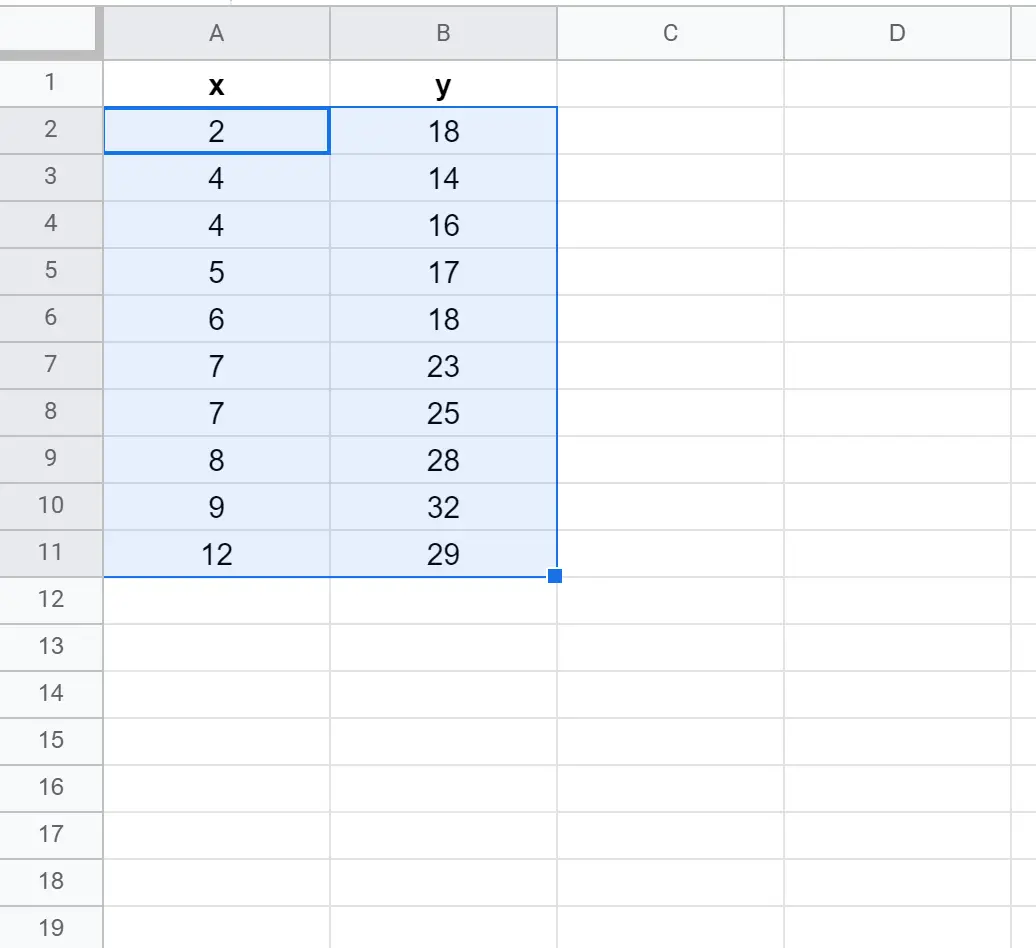
首先，让我们创建一个具有以下值的假数据集：

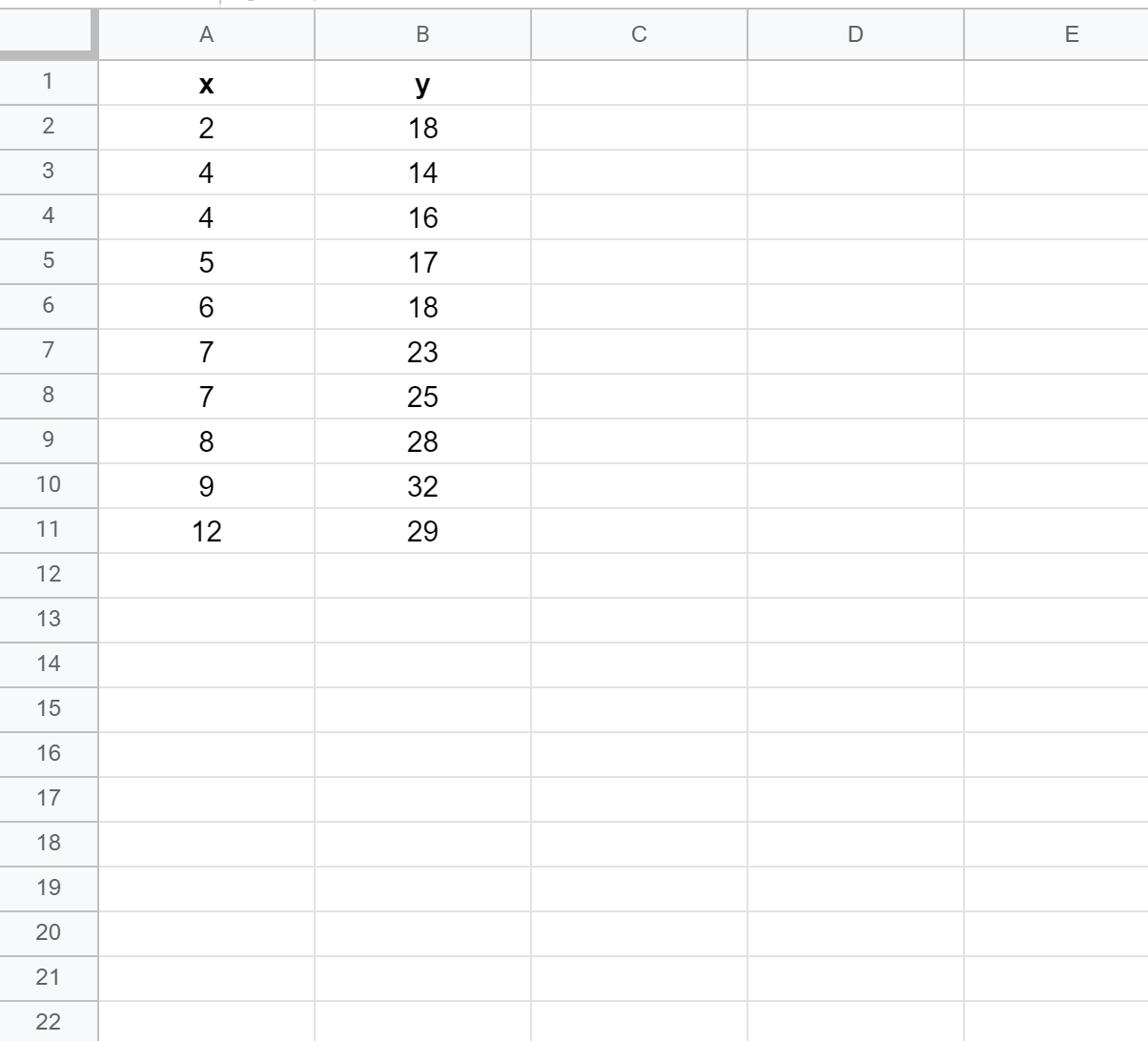
第 2 步：创建散点图

接下来，我们将创建散点图来可视化数据。

首先，突出显示单元格A2:B11 ，如下所示：

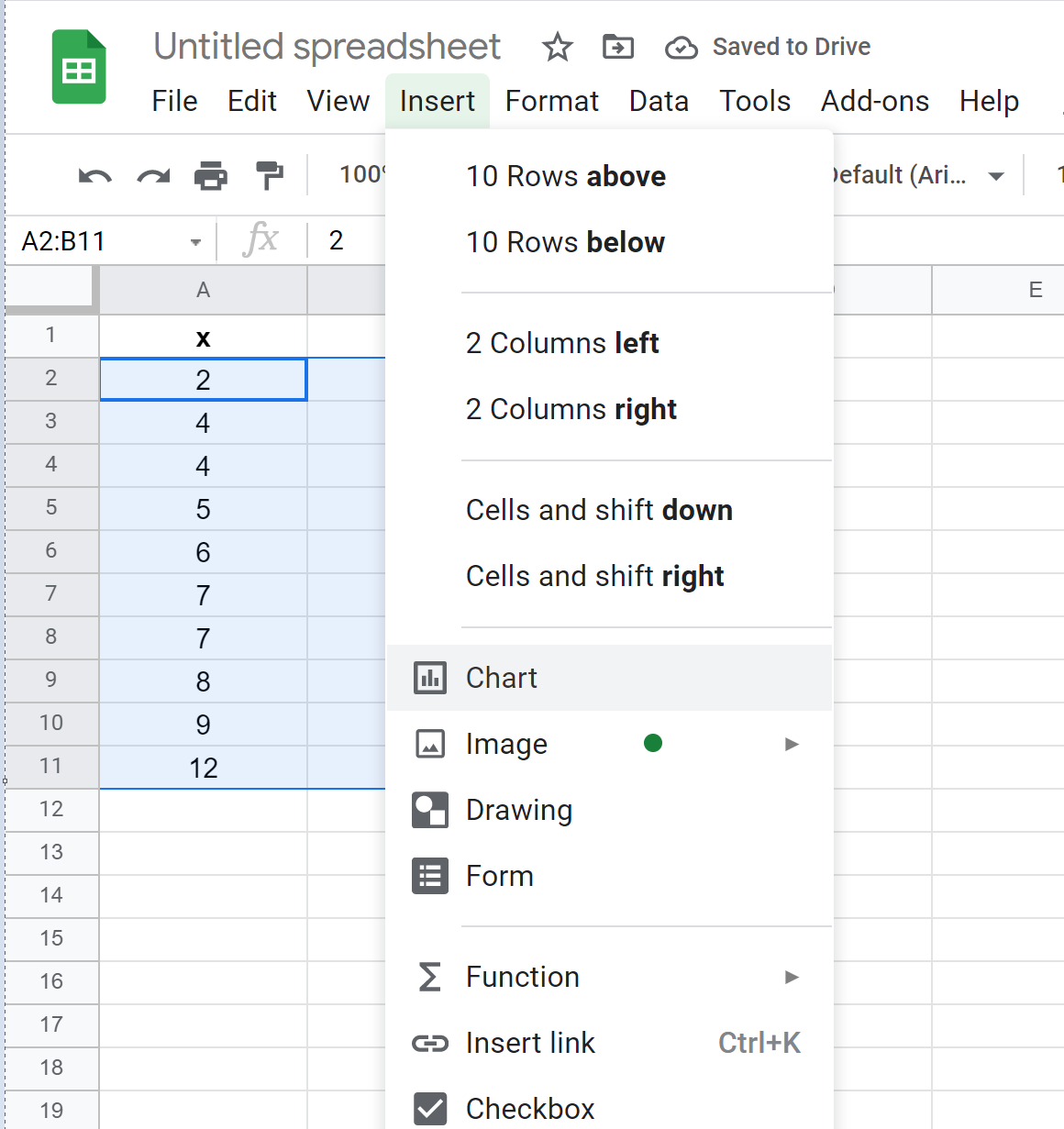
接下来，单击“插入”选项卡，然后从下拉菜单中单击“图表” ：

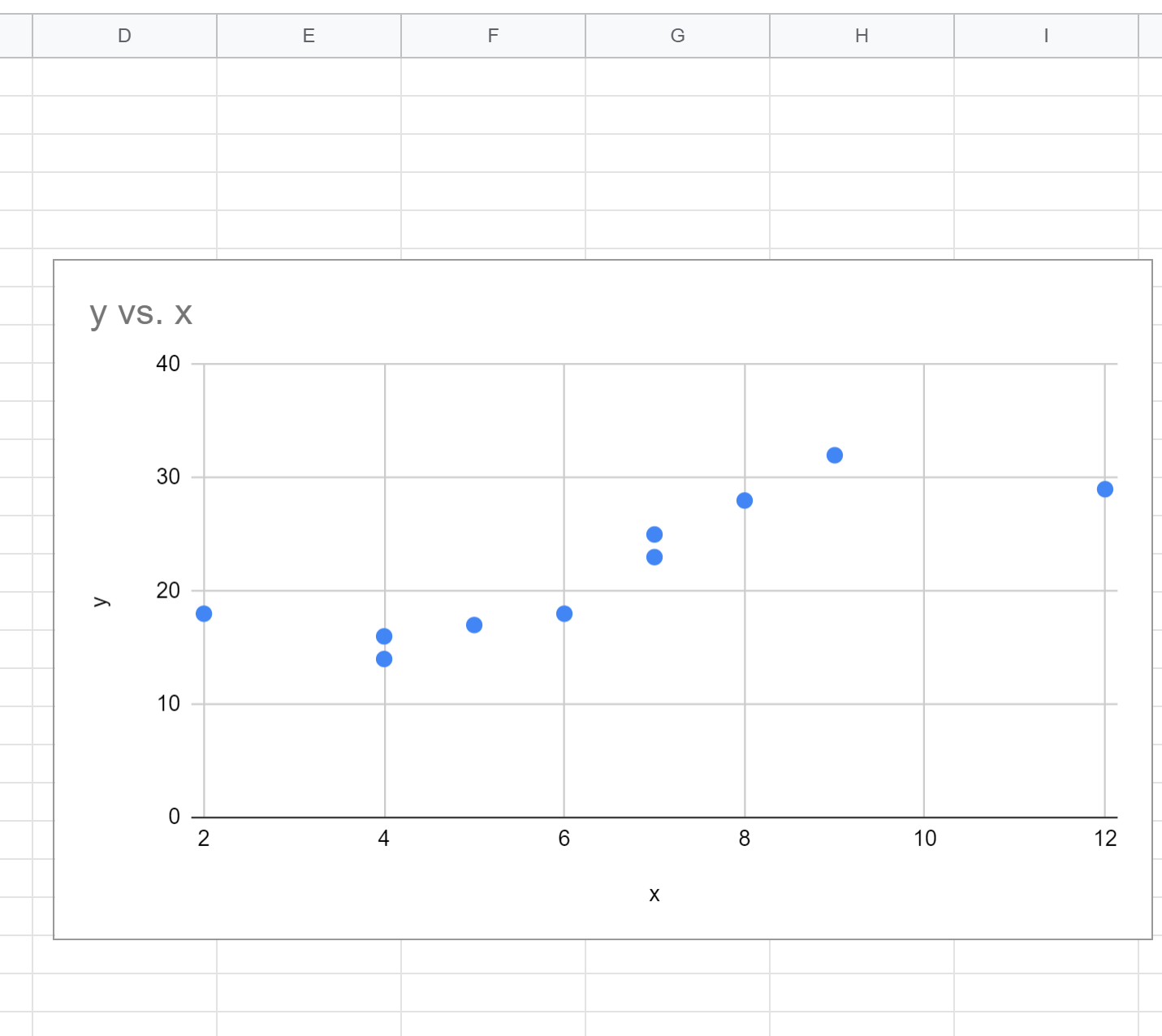
默认情况下，Google 表格会插入散点图：

第三步：求多项式回归方程

接下来，双击散点图上的任意位置以在右侧显示图形编辑器窗口：

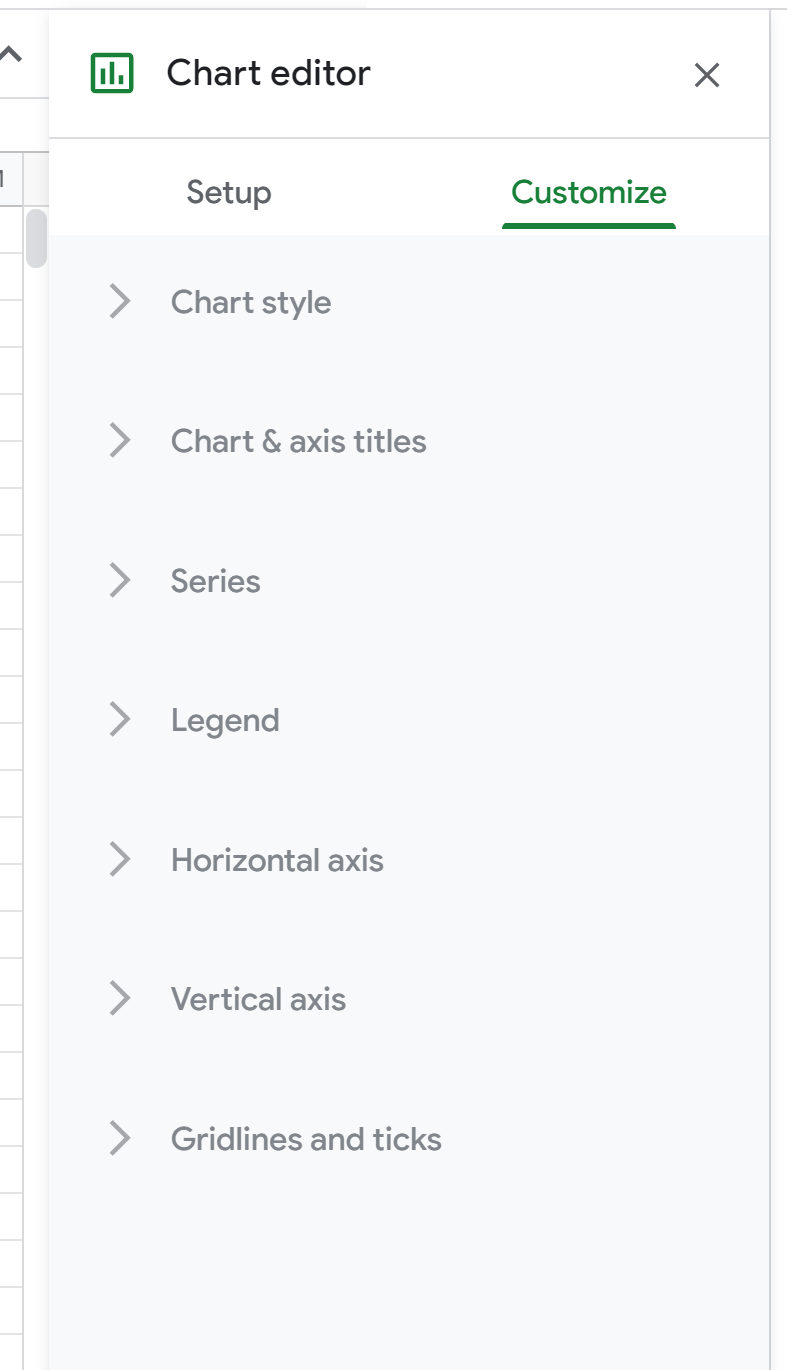
接下来，单击系列。接下来，向下滚动并选中Trendline旁边的框，并将 Type 更改为Polynomial 。对于“标签”，选择“使用方程” ，然后选中“显示^R2”旁边的框。

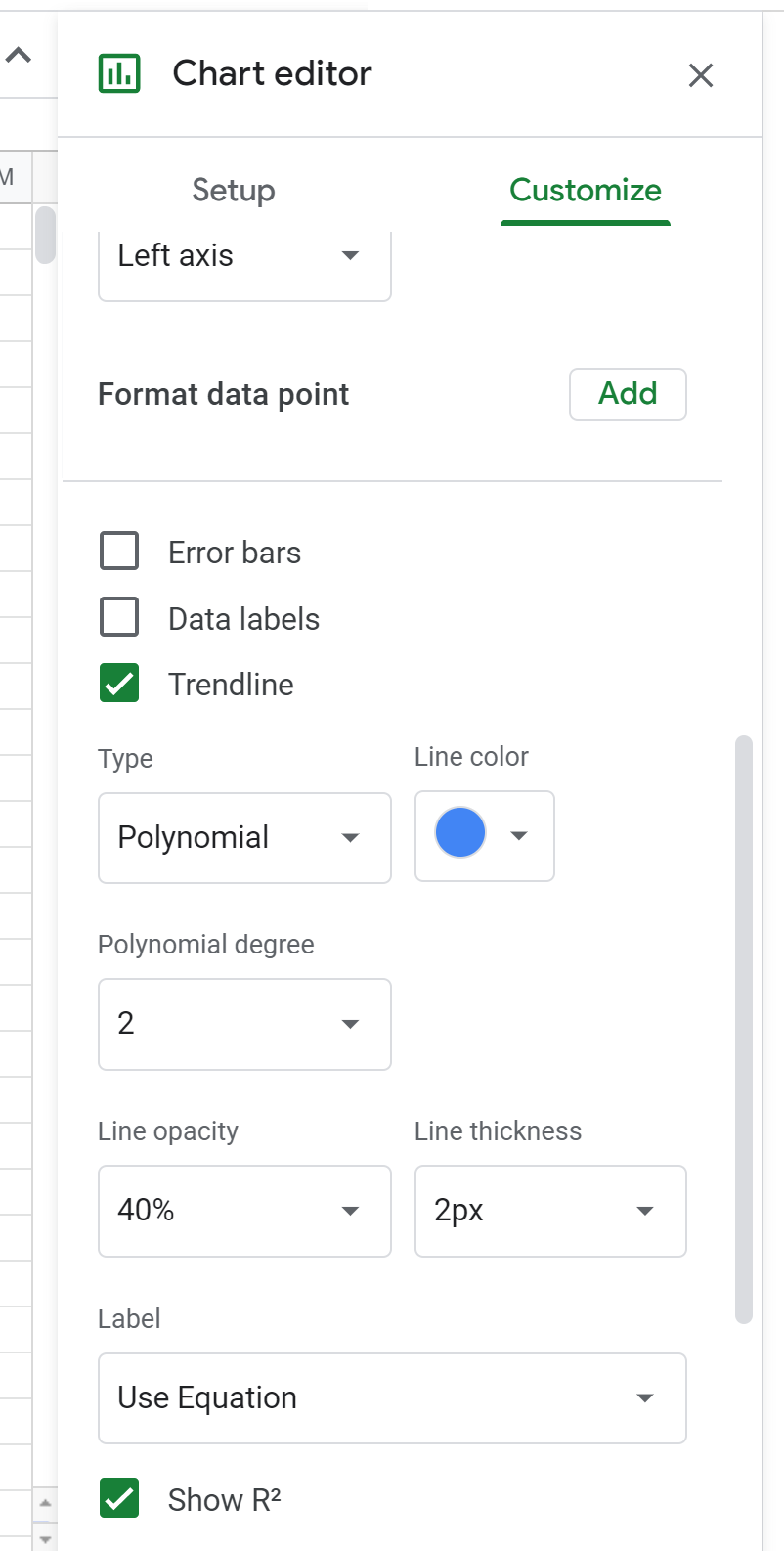
这将导致以下公式出现在散点图上方：

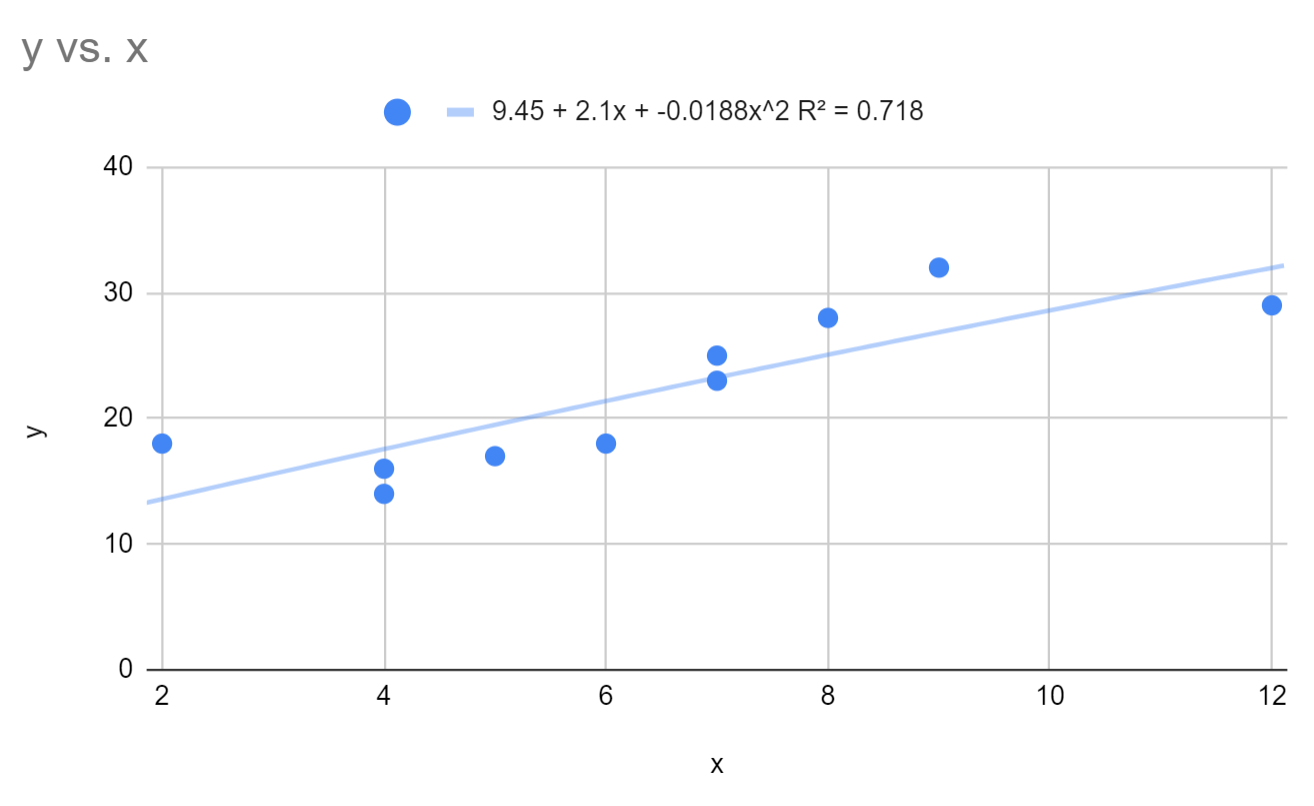
我们可以看到拟合的多项式回归方程为：

y = 9.45 + 2.1x – 0.0188x ²

该模型的 R 平方为0.718 。

回想一下， R 平方告诉我们可以由预测变量解释的响应变量的变化百分比。值越高，模型越好。

接下来，在图形编辑器中将多项式的次数更改为 3：

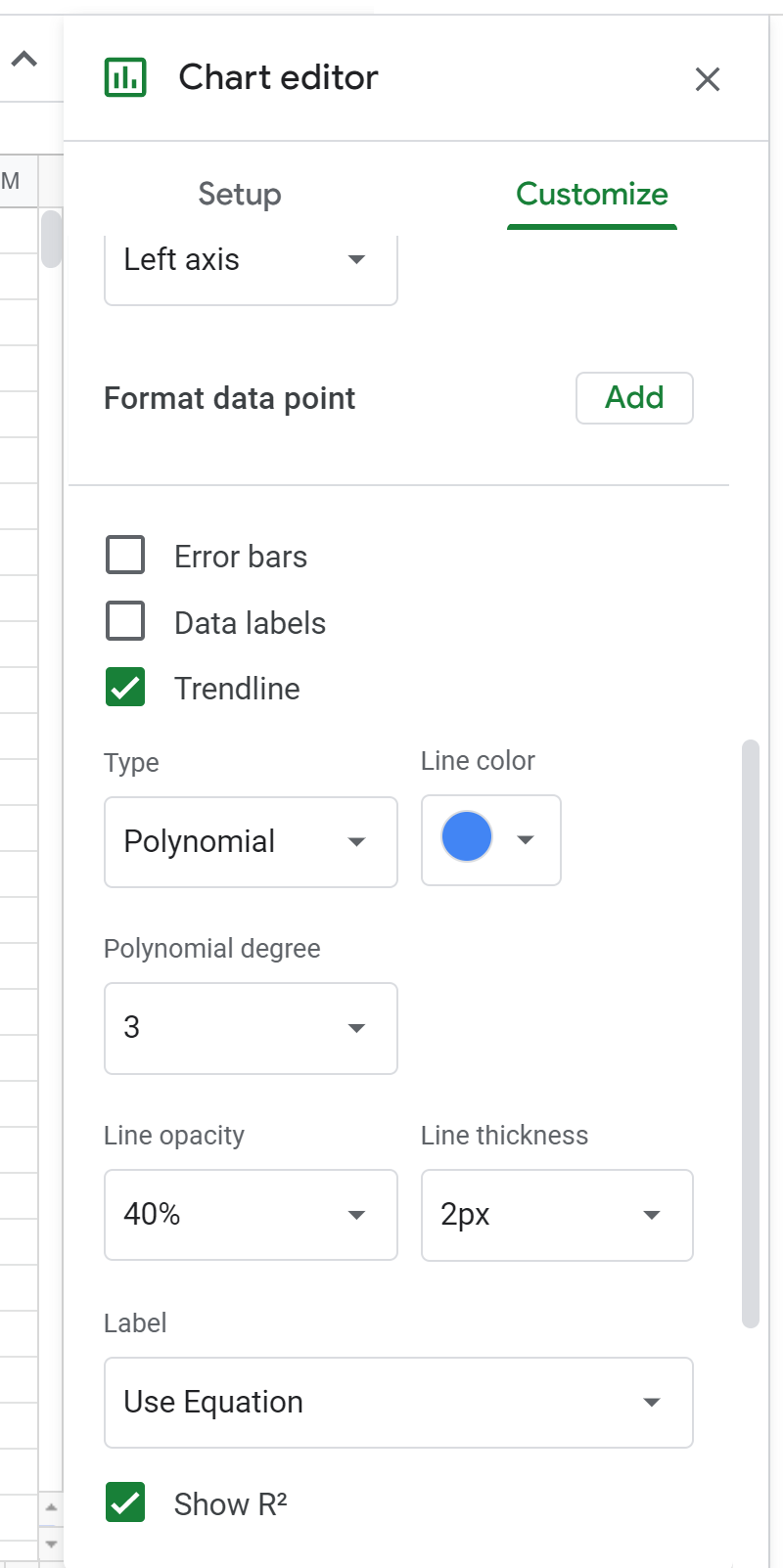
这将导致以下公式出现在散点图上方：

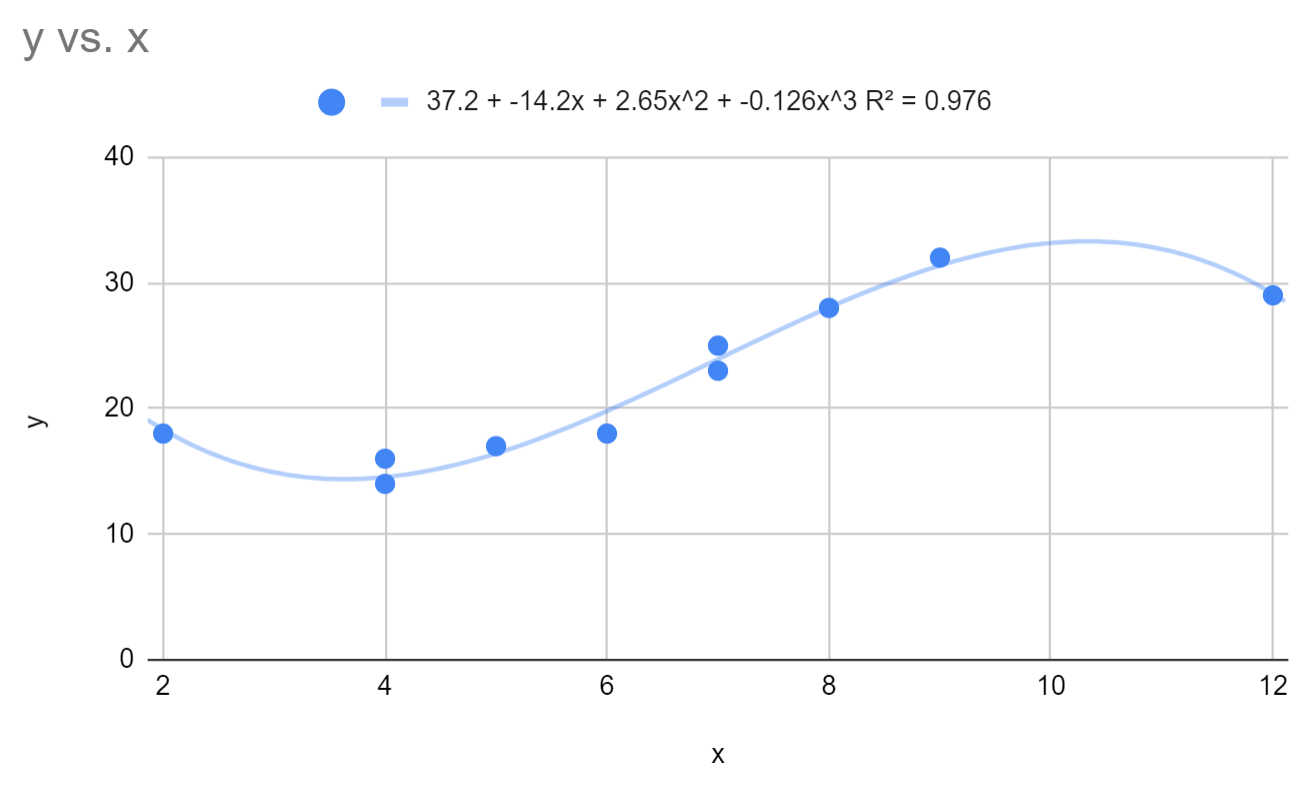
这将拟合的多项式回归方程更改为：

y = 37.2 – 14.2x + 2.64x ² – 0.126x ³

该模型的 R 平方为0.976 。

请注意，该模型的 R 平方明显高于次数为 2 的多项式回归模型。这表明该回归模型在捕获基础数据的趋势方面明显更好。

如果将多项式的次数更改为 4，R 平方几乎不会增加到0.981 。这表明 3 次多项式回归模型足以捕捉这些数据的趋势。

我们可以使用拟合回归方程来找到给定预测变量值的响应变量的期望值。例如，如果x = 4，则y的预期值为：

y = 37.2 – 14.2(4) + 2.64(4) ² – 0.126(4) ³ = 14.576

您可以在此页面上找到其他 Google 表格教程。