什么被认为是好的残差图或坏的残差图?
在回归分析中,残差图是一种在 x 轴上显示回归模型的拟合值并沿 y 轴显示模型残差的图。
当目视检查剩余布局时,我们通常会通过两件事来确定布局是“好”还是“坏”:
1. 残差是否显示出明显的趋势?
- 在“良好”的残差图中,残差没有显示出明显的趋势。
- 在“坏”残差图中,残差具有某种类型的模式,例如曲线或波浪。这表明我们使用的回归模型没有提供对数据的适当拟合。
2. 残差的方差是否系统地增加或减少?
- 在“良好”残差图中,残差随机分散在零附近,方差没有系统增加或减少。
- 在“坏”残差图中,残差的方差系统地增加或减少。
如果残差图被评为“良好”,则意味着我们可以信任回归模型的结果并且可以安全地解释模型系数。
但是,如果残差图被评为“不良”,则意味着模型结果不可靠,我们需要对数据拟合不同的回归模型。
以下示例解释了如何在实践中解释“好”和“坏”残差图。
示例 1:“良好”残留痕迹
假设我们拟合回归模型并获得以下残差图:
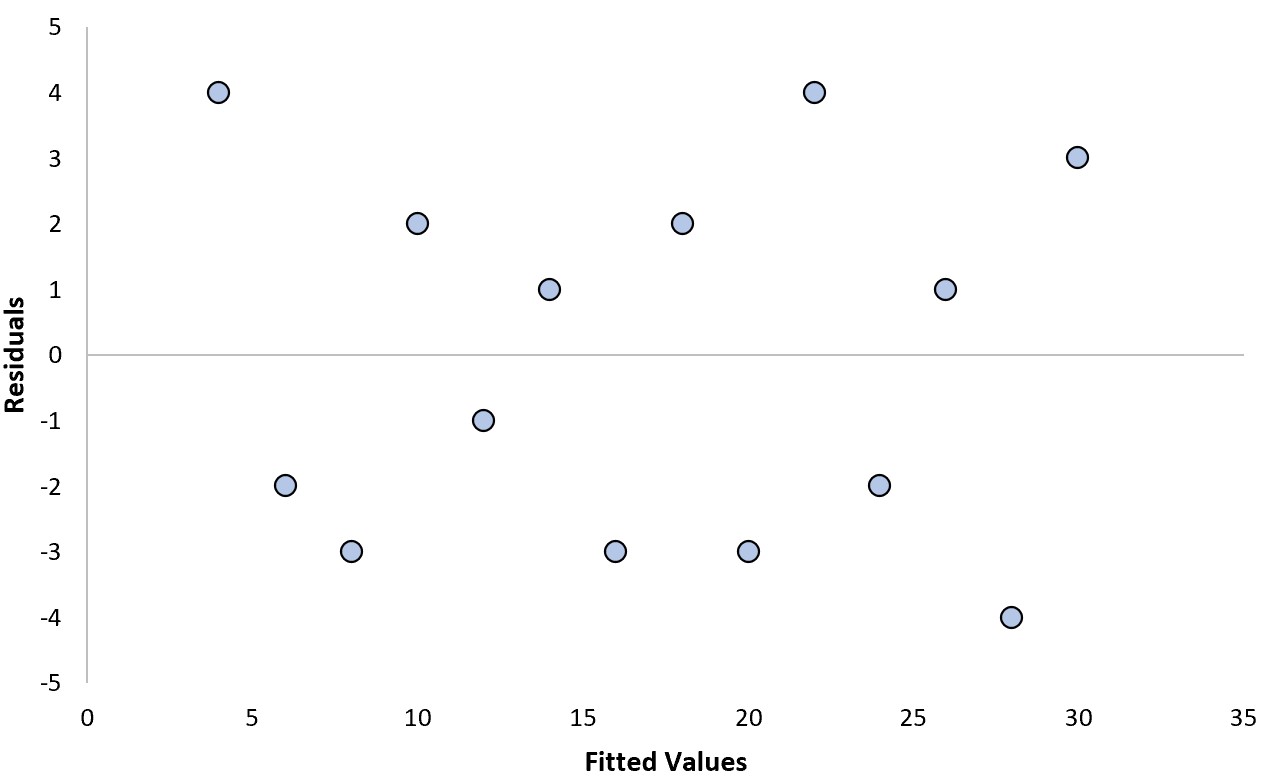
我们可以回答以下两个问题来确定这是否是一个“好的”残差图:
1. 残差是否显示出明显的趋势?
不会。残差随机散布在零附近,没有清晰的模式。
2. 残差的方差是否系统地增加或减少?
不会。在拟合值的每个级别,残差具有相当恒定的方差(即残差与零值之间的距离)。
由于我们对这两个问题的回答都是“否”,因此我们认为这是一个“好的”残差图。
因此,我们可以信任回归模型的结果并安全地解释模型系数。
示例 2:具有清晰模型的“糟糕”残差图
假设我们拟合回归模型并获得以下残差图:
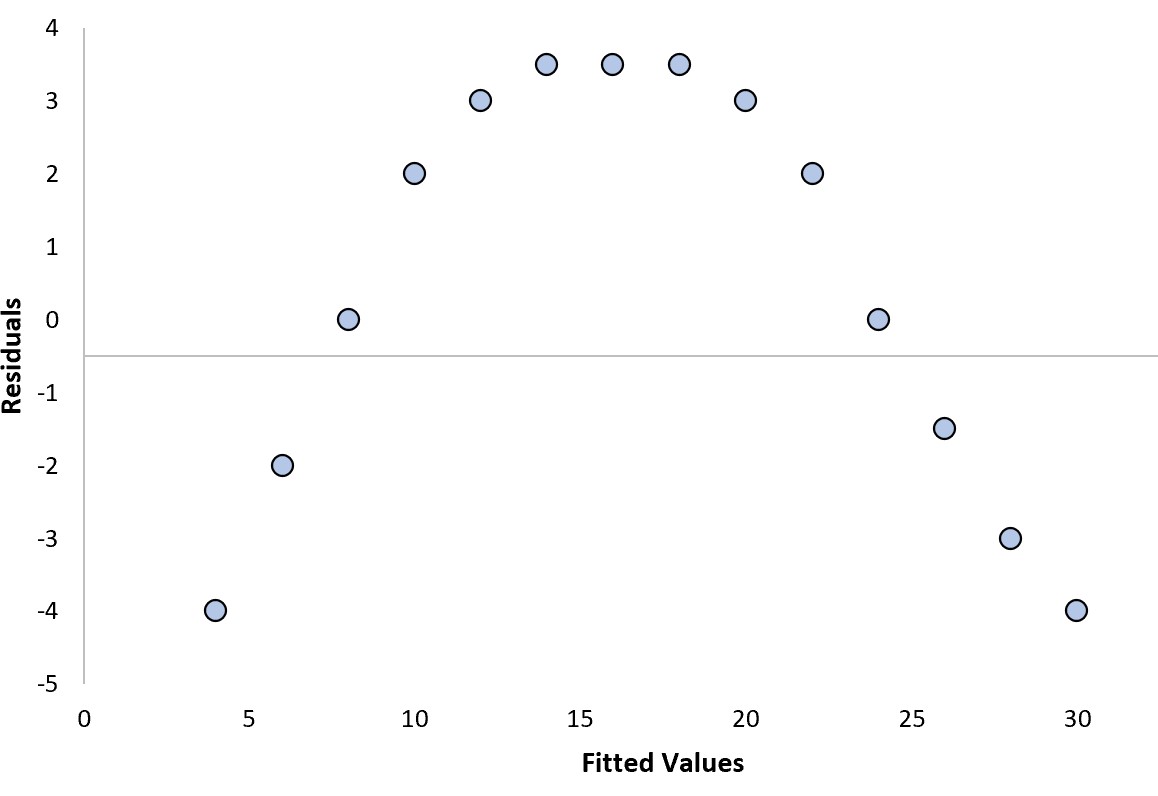
我们可以回答以下两个问题来确定这是否是一个“好的”残差图:
1. 残差是否显示出明显的趋势?
是的。残留物呈现出弯曲的图案。
2. 残差的方差是否系统地增加或减少?
是的。残差在不同水平的拟合值上具有不同水平的方差。
由于我们对这些问题中的至少一个回答“是”,因此我们会认为这是一个“糟糕”的残差图。
这意味着回归模型不能很好地拟合数据。
特别是,残差图中的曲线模式表明线性回归模型无法拟合数据,而二次回归模型可能会做得更好。
示例 3:方差增加的“坏”残差图
假设我们拟合回归模型并获得以下残差图:
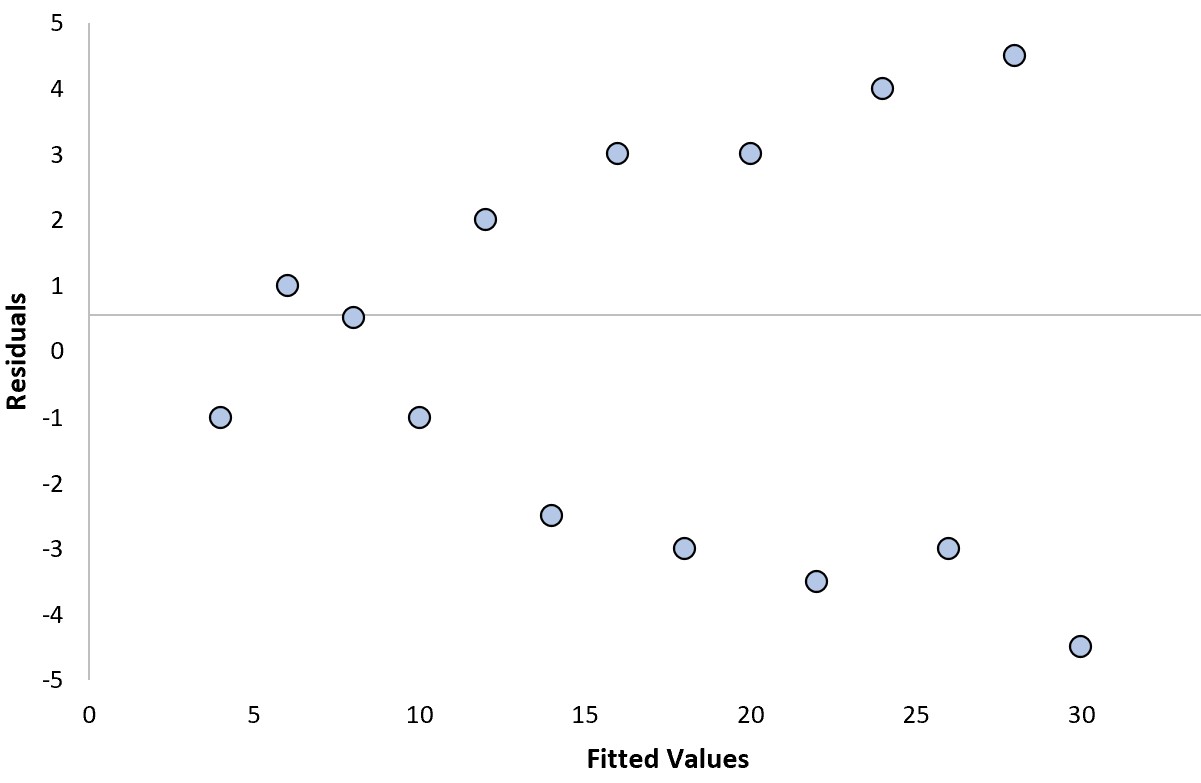
我们可以回答以下两个问题来确定这是否是一个“好的”残差图:
1. 残差是否显示出明显的趋势?
不。残差没有明显的趋势。
2. 残差的方差是否系统地增加或减少?
是的。残差的方差随着拟合值的增加而增加。
由于我们对这些问题中的至少一个回答“是”,因此我们会认为这是一个“糟糕”的残差图。
在这个特定的例子中,残差受到异方差的影响,它是指在不同的拟合值水平上残差的方差不相等。
这意味着回归模型的结果可能不可靠。
请参阅本文,了解解决回归模型中异方差问题的不同方法。
其他资源
以下教程解释了如何使用不同的统计软件创建残差图: