如何在excel中计算vif
当两个或多个解释变量彼此高度相关,以致它们在回归模型中不提供唯一或独立的信息时,就会出现回归分析中的多重共线性。如果变量之间的相关程度足够高,则在拟合和解释回归模型时可能会出现问题。
幸运的是,可以使用称为方差膨胀因子 (VIF)的指标来检测多重共线性,该指标测量回归模型中解释变量之间的相关性和相关强度。
本教程介绍如何在 Excel 中计算 VIF。
示例:在 Excel 中计算 VIF
对于此示例,我们将使用以下描述 10 名篮球运动员属性的数据集执行多元线性回归。我们将使用评分作为响应变量,并使用得分、助攻和篮板作为解释变量来拟合回归模型。接下来,我们将确定每个解释变量的 VIF 值。
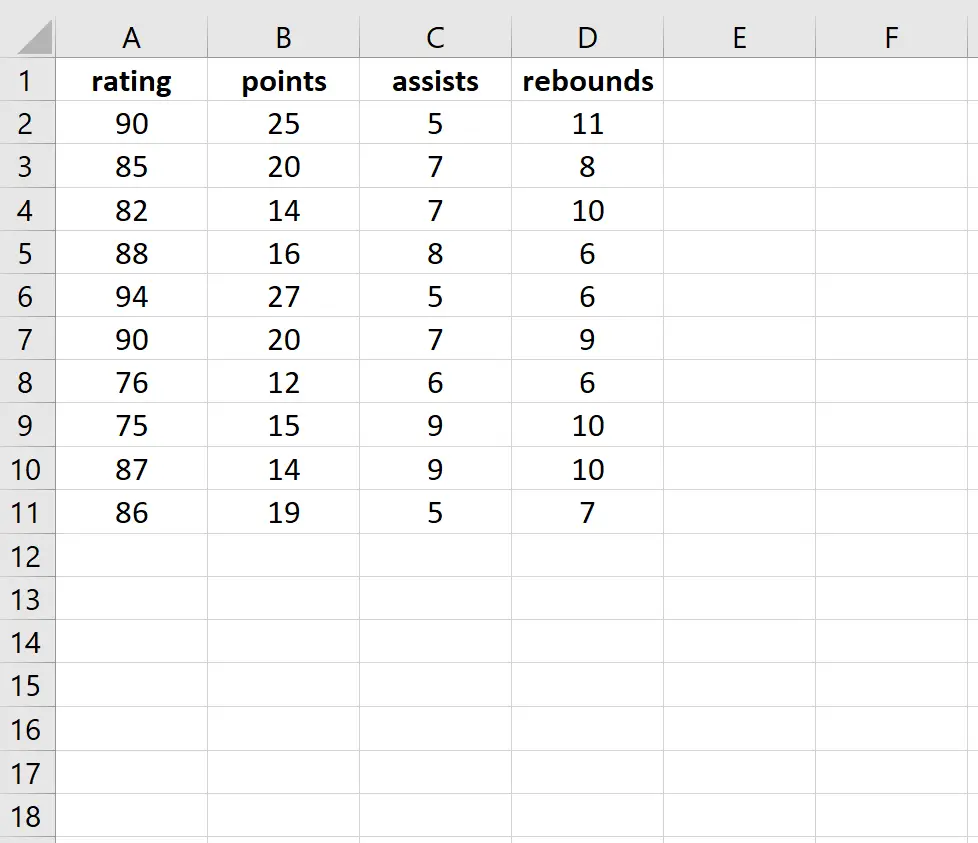
步骤 1:执行多元线性回归。
在顶部功能区上,转到“数据”选项卡,然后单击“数据分析”。如果您没有看到此选项,则必须首先安装免费的分析工具库软件。

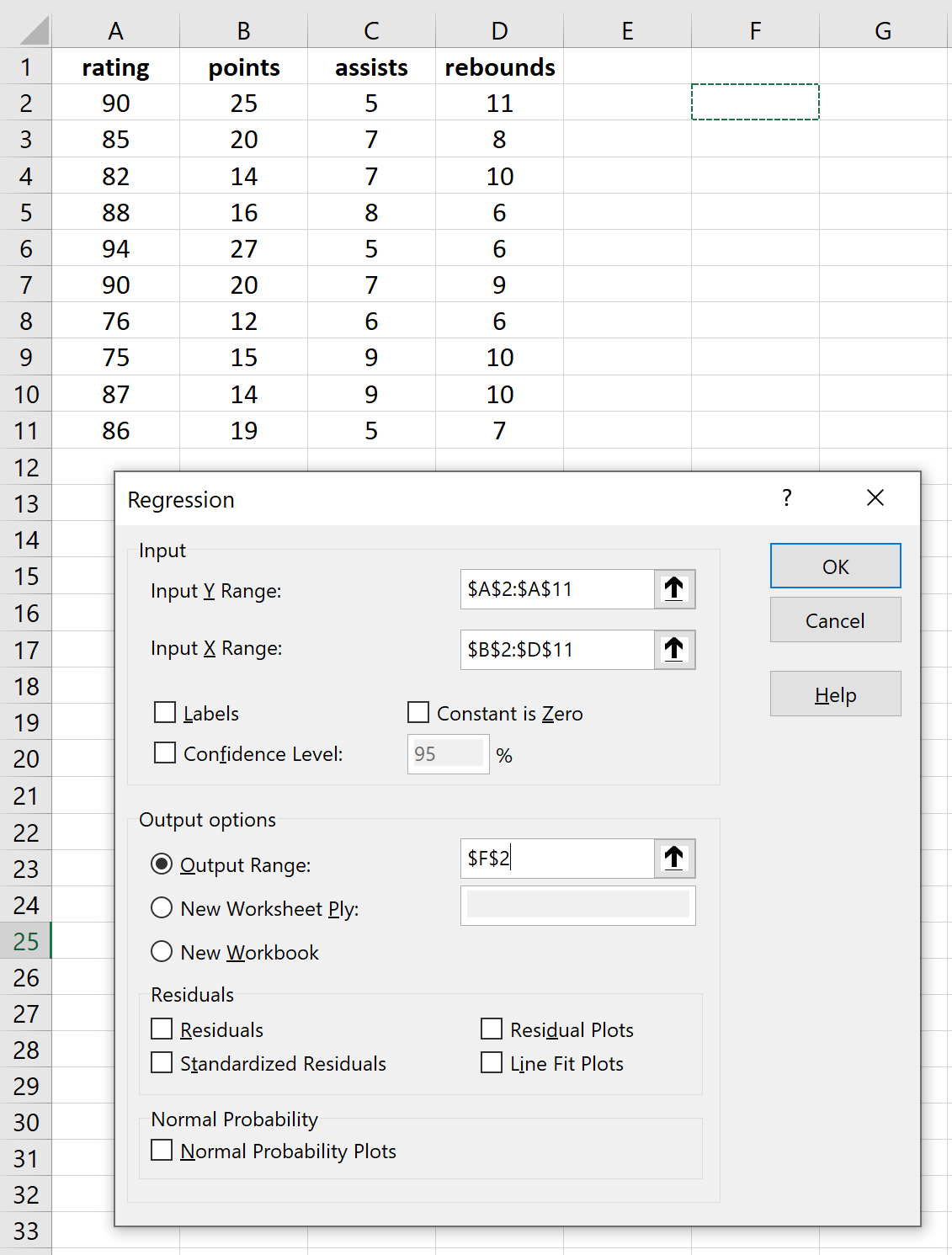
单击“数据分析”后,将出现一个新窗口。选择回归并单击确定。

填写响应变量和解释变量的必要表格,然后单击“确定”。
这会产生以下结果:
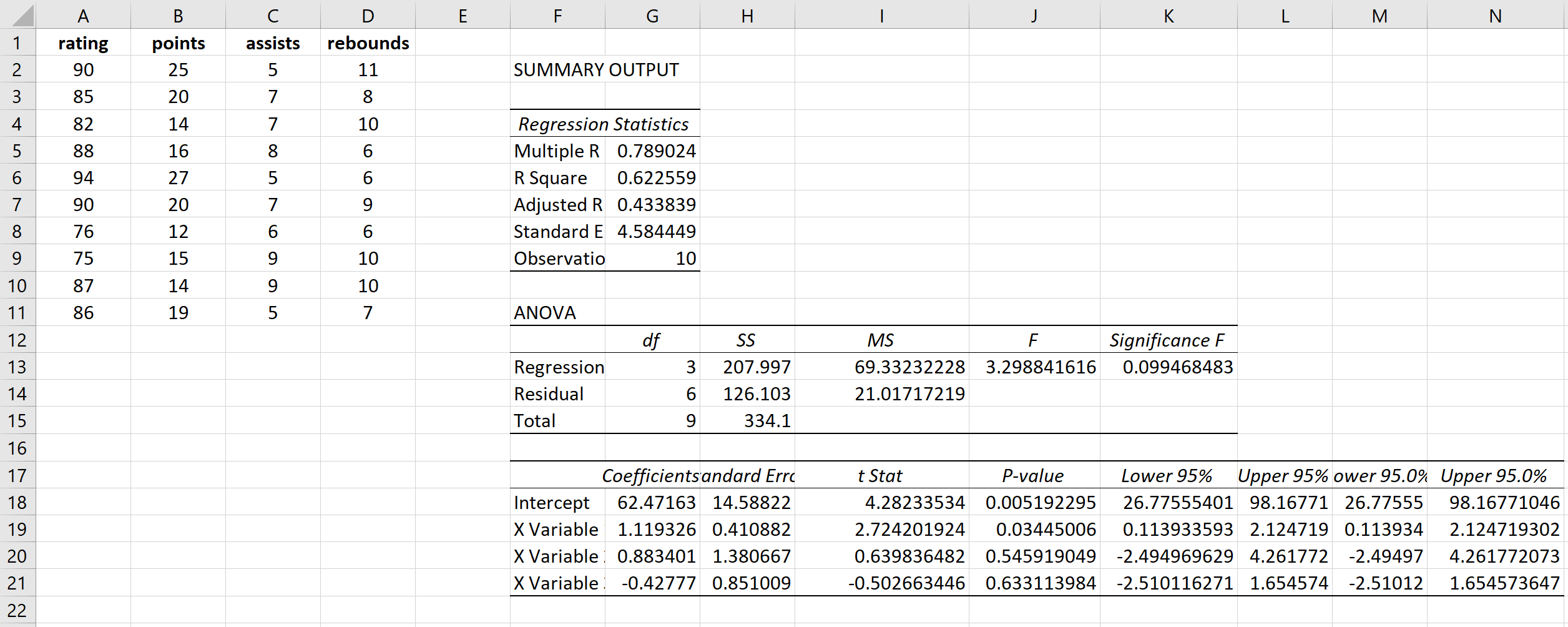
步骤 2:计算每个解释变量的 VIF。
接下来,我们可以通过使用一个解释变量作为响应变量、另外两个作为解释变量执行单独回归来计算三个解释变量中每一个的 VIF。
例如,我们可以通过使用得分作为响应变量、助攻和篮板作为解释变量执行多元线性回归来计算得分变量的 VIF。
这会产生以下结果:

点的 VIF 计算公式为 1 / (1 – R Square) = 1 / (1 – .433099) = 1.76 。
然后我们可以对其他两个变量(助攻和篮板)重复此过程。
事实证明,三个解释变量的 VIF 如下:
积分: 1.76
助攻: 1.96
篮板数: 1.18
如何解释 VIF 值
VIF 值从 1 开始,没有上限。解释 VIF 的一般规则是:
- 值为 1 表示给定解释变量与模型中的任何其他解释变量之间不存在相关性。
- 1 到 5 之间的值表示给定解释变量与模型中的其他解释变量之间存在中等相关性,但通常没有严重到需要特别注意的程度。
- 大于 5 的值表示给定解释变量与模型中的其他解释变量之间可能存在严重相关性。在这种情况下,回归结果中的系数估计和 p 值可能不可靠。
由于我们的回归模型中解释变量的每个 VIF 值都接近于 1,因此多重共线性在我们的示例中不是问题。