完整指南:如何报告方差分析结果
单向方差分析用于确定三个或更多独立组的平均值之间是否存在统计显着差异。
在报告单向方差分析的结果时,我们始终使用以下一般结构:
- 自变量和因变量的简要描述。
- 方差分析的总体 F 值和相应的 p 值。
- 事后比较的结果(如果 p 值具有统计显着性)。
这是我们可以使用的确切措辞:
进行单向方差分析来比较[自变量]对[因变量]的影响。
单向方差分析显示,至少两组之间的[因变量]存在统计显着性差异(F(组间 df,组内 df)= [F 值],p = [p -价值])。
Tukey 的多重比较 HSD 检验显示,[因变量] 的平均值在 [组名称] 和 [组名称] 之间显着不同(p = [p 值],95% CI = [下,上])。
[组名称]和[组名称]之间没有统计学上的显着差异(p = [p值])。
以下示例展示了如何在实践中报告单向方差分析的结果。
示例:报告单向方差分析的结果
假设一名研究人员招募 30 名学生参加一项研究。学生被随机分配使用三种学习技巧中的一种来准备下个月的考试。月底,所有学生都参加相同的考试。
然后,研究人员进行单向方差分析,以确定三组之间的平均考试成绩是否存在差异。
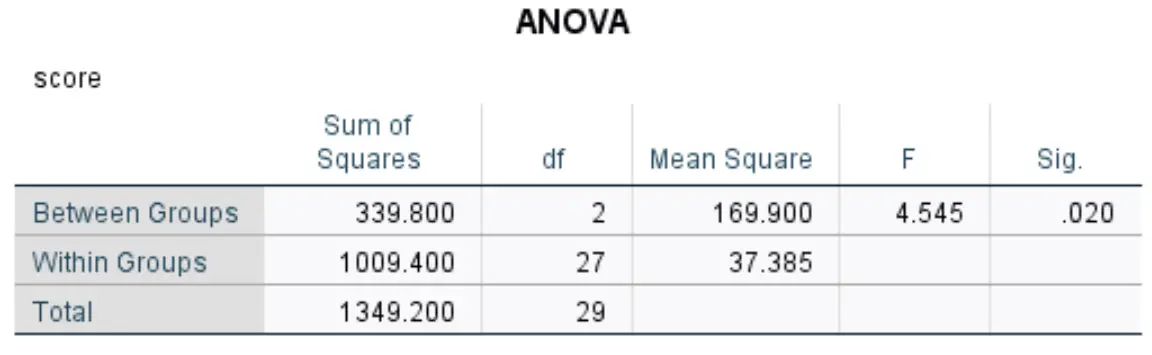
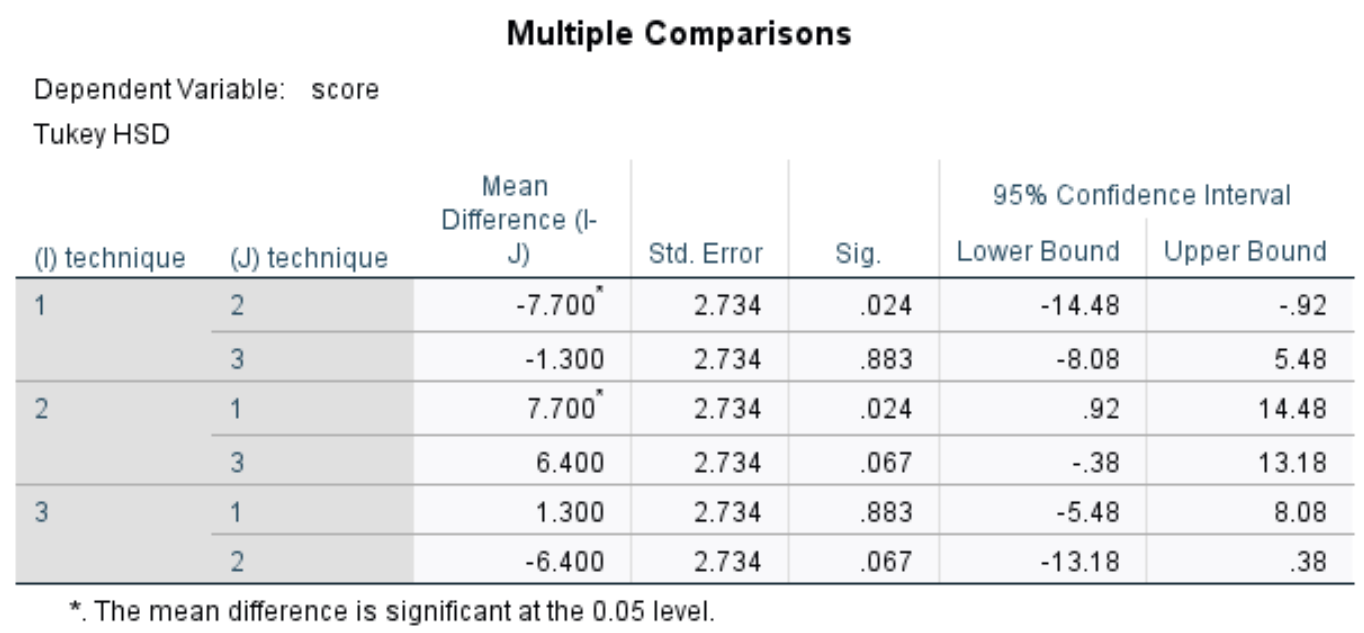
下表列出了单向方差分析的结果以及 Tukey 的事后多重比较表:
以下是报告单向方差分析结果的方法:
进行单向方差分析来比较三种不同研究技术对检查结果的影响。
单向方差分析显示,至少两组之间的平均考试成绩存在统计显着性差异 (F(2,27) = [4.545],p = 0.02)。
Tukey 的 HSD 多重比较测试显示,技术 1 和技术 2 之间的考试成绩平均值存在显着差异 (p = 0.024,95% CI = [-14.48,-0. 92])。
技术 1 和技术 3 之间(p = 0.883)或技术 2 和技术 3 之间(p = 0.067)之间的平均考试成绩没有统计学上的显着差异。
要记住的事情
报告单向方差分析结果时需要记住以下几点:
使用描述性统计表。
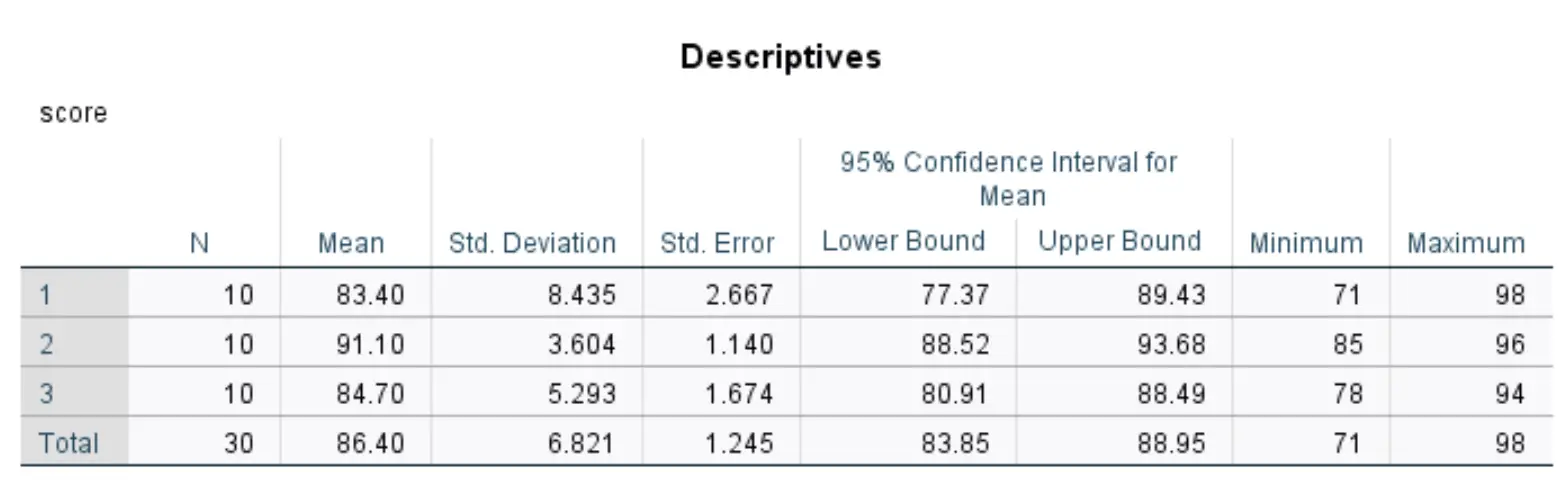
提供一个描述性统计表可能会有所帮助,该表还显示每个治疗组中值的平均值和标准差,以便让读者更完整地了解数据。
例如,SPSS 生成以下描述性统计表,显示三个学习技能组中每个组的学生考试成绩的平均值和标准差:
仅在必要时报告事后结果。
如果方差分析的总体 p 值不具有统计显着性,您将不会在组之间执行事后多重比较。这意味着您显然不需要在最终报告中报告事后结果。
如果您需要执行事后测试,最常用的是 Tukey HSD 测试,但有时您也可以使用Scheffe 或 Bonferroni 测试来代替。
如有必要,对 p 值进行舍入。
通常,为了简洁起见,方差分析结果中的总体 F 值和所有 p 值都会四舍五入到小数点后两位或三位。
无论您选择使用多少位小数,请务必在整个报告中保持一致。
其他资源
以下教程解释了如何以 APA 格式报告其他统计测试和过程:
如何报告双向方差分析结果(附示例)
如何报告克朗巴赫阿尔法(附示例)
如何报告 t 检验结果:示例
如何报告卡方结果:举例
如何报告皮尔逊相关性:举例
如何报告回归结果:举例